【信号处理】LQ/QR 噪声估计器（Matlab实现)-优快云博客

“在代码的海洋里，有无尽的知识等待你去发现。我就是那艘领航的船，带你乘风破浪，驶向代码的彼岸。

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

💥1 概述

LQ/QR 噪声估计器是一种用于估计噪声的工具。在信号处理和数据分析等领域，准确估计噪声水平对于许多任务至关重要。噪声的存在会干扰对真实信号的观测和分析，降低系统性能。LQ/QR 噪声估计器通过特定的算法和技术来估计噪声的特性。 LQ/QR 噪声估计器可能基于线性二次（LQ）或正交三角分解（QR）等数学方法。这些方法利用输入数据的统计特性和特定的数学变换来提取噪声的信息。它可以应用于各种场景，例如通信系统中的信道噪声估计、图像和音频处理中的噪声去除、传感器数据的去噪等。通过准确估计噪声，后续可以采取相应的措施来降低噪声的影响，提高信号的质量和可靠性。总之，LQ/QR 噪声估计器为解决噪声估计问题提供了一种有效的途径，有助于提高系统的性能和数据的准确性。

📚2 运行结果

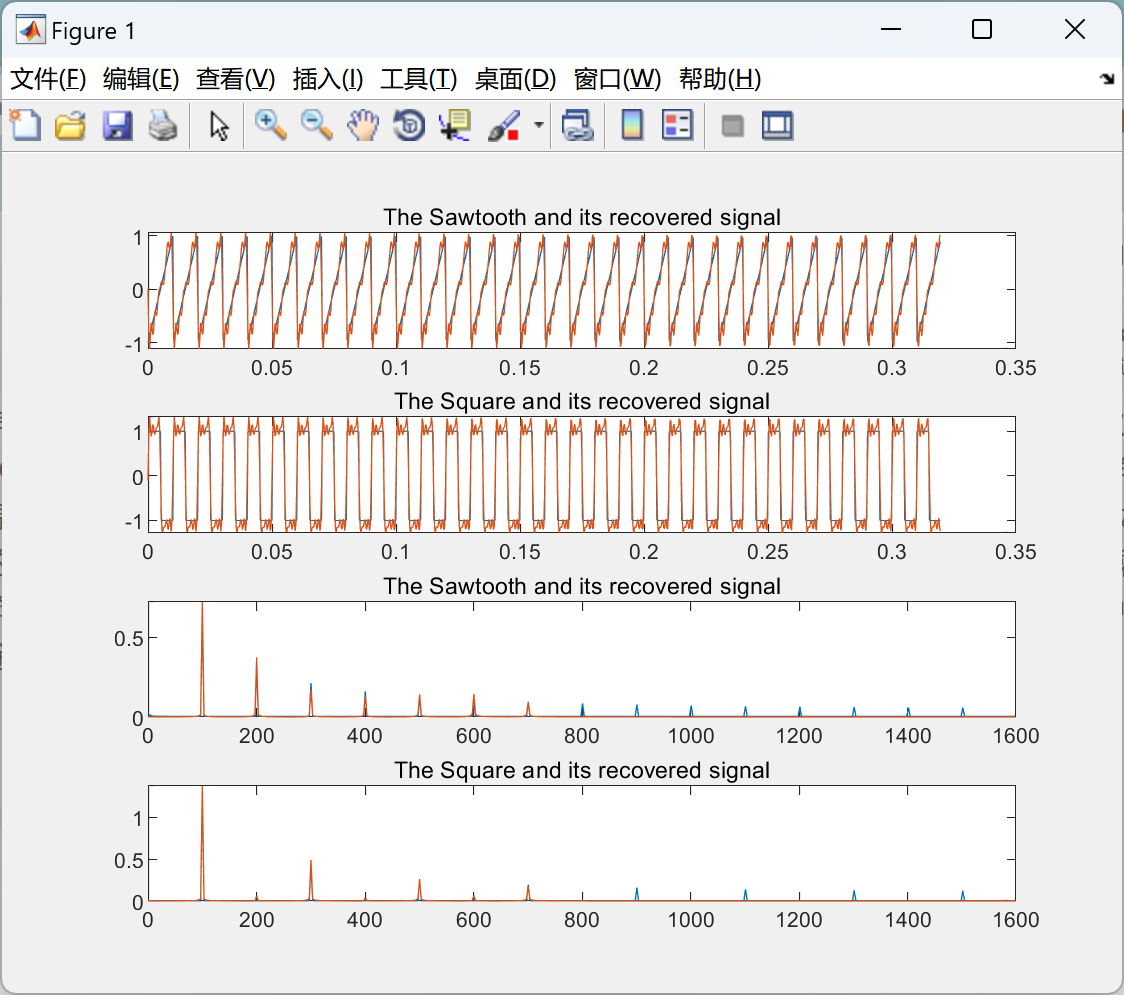
主函数部分代码：

%In this example, QR noise estimation is used to recover
% two signals from a background noise.

% The tageted signals have a fundamental frequency at 100Hz
% and a number of harmonics at 200, 300, ..., 700Hz.

% 1. Create the trageted signals:
t=[0:1023]'*(1/3202);
S1=sawtooth(2*pi*100*t);
S2=square(2*pi*100*t);

% 2. Add a random noise:
O1=S1+randn(1024,1);
O2=S2+randn(1024,1);

% 3. Recover the targeted signals using QR noise estimation:
R1=QR_noise_estimation(O1,[100:100:700]);
R2=QR_noise_estimation(O2,[100:100:700]);

% Plot the time-series results:
subplot(411);plot([t t],[S1 R1])
title('The Sawtooth and its recovered signal')
subplot(412);plot([t t],[S2 R2])
title('The Square and its recovered signal')

% Obtain the frequency domain of results:
f=linspace(0,3201,1024)';
f=f(1:512);
F1=abs(fft([S1 R1])/512);
F1=F1(1:512,:);
F2=abs(fft([S2 R2])/512);
F2=F2(1:512,:);

% MSE performance:
MSE=[sqrt(mean((S1-R1).^2)), sqrt(mean((S2-R2).^2))]

% Plot the frequency domain results:
subplot(413);plot([f f],F1)
title('The Sawtooth and its recovered signal')
subplot(414);plot([f f],F2)
title('The Square and its recovered signal')

🎉3 参考文献

文章中一些内容引自网络，会注明出处或引用为参考文献，难免有未尽之处，如有不妥，请随时联系删除。

[1]Cao Y ,Wu X ,Qi S , et al. Pseudo-ISP: Learning pseudo in-camera signal processing pipeline from a color image denoiser[J]. Neurocomputing,2024,605.

[2]吴晓欢,李嘉宁.基于图信号处理的多声源定位方法研究[J/OL].信号处理:1-16[2024-09-03].http://kns.cnki.net/kcms/detail/11.2406.TN.20240823.1724.011.html.