【带宽感知自适应模式分解】铁路轴承故障诊断的带宽感知自适应模式分解（Matlab代码实现）

 💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码实现

---

💥1 概述

带宽感知自适应模式分解（Bandwidth-Aware Adaptive Mode Decomposition，BAAMD）是一种用于信号处理和特征提取的方法。在铁路轴承故障诊断中，BAAMD可以帮助提取出信号中蕴含的有关轴承运行状态和故障特征的信息。

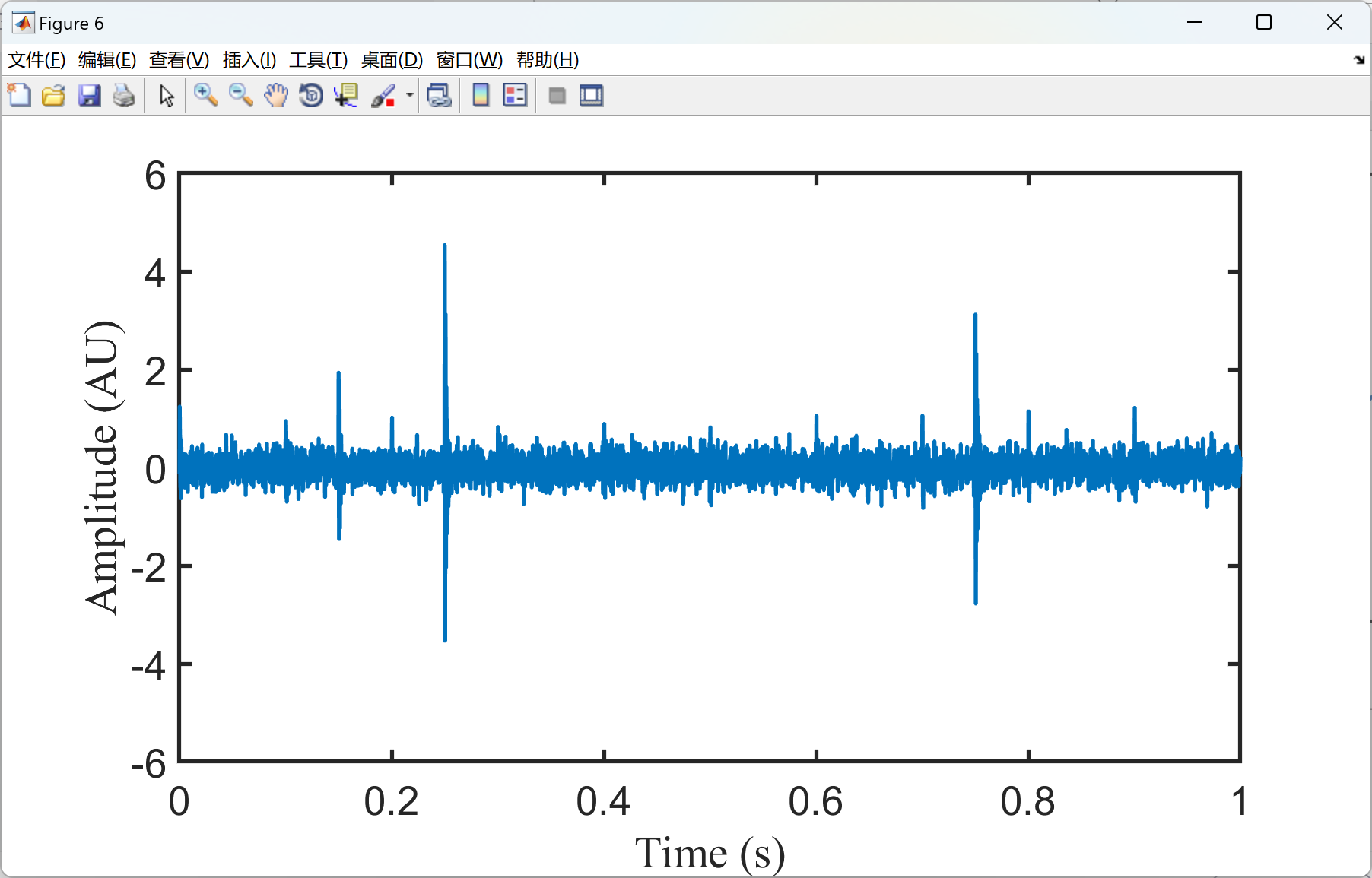
具体来说，铁路轴承在运行过程中会产生振动信号，这些信号包含了轴承的工作状态和可能存在的故障信息。通过应用带宽感知自适应模式分解，可以将振动信号分解成多个不同频率的子信号，每个子信号对应着不同的运行模式或特征。这样一来，就能更好地分析和识别出轴承的运行状态，判断是否存在故障，并进一步进行诊断和预测。

总的来说，带宽感知自适应模式分解在铁路轴承故障诊断中的应用，有助于提高对轴承振动信号的分析效率和准确性，从而更好地保障铁路设备的正常运行和安全性。

📚2 运行结果

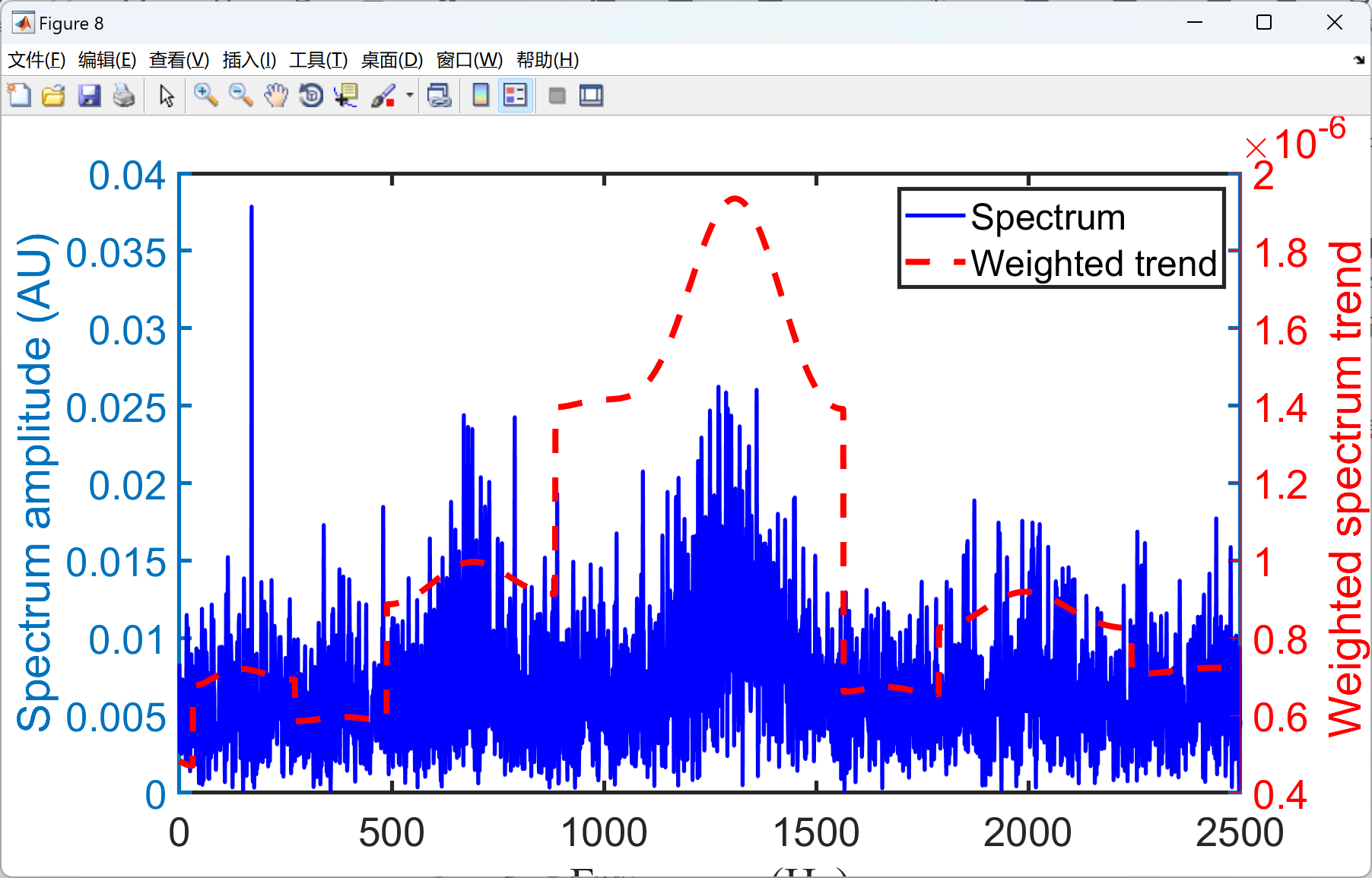
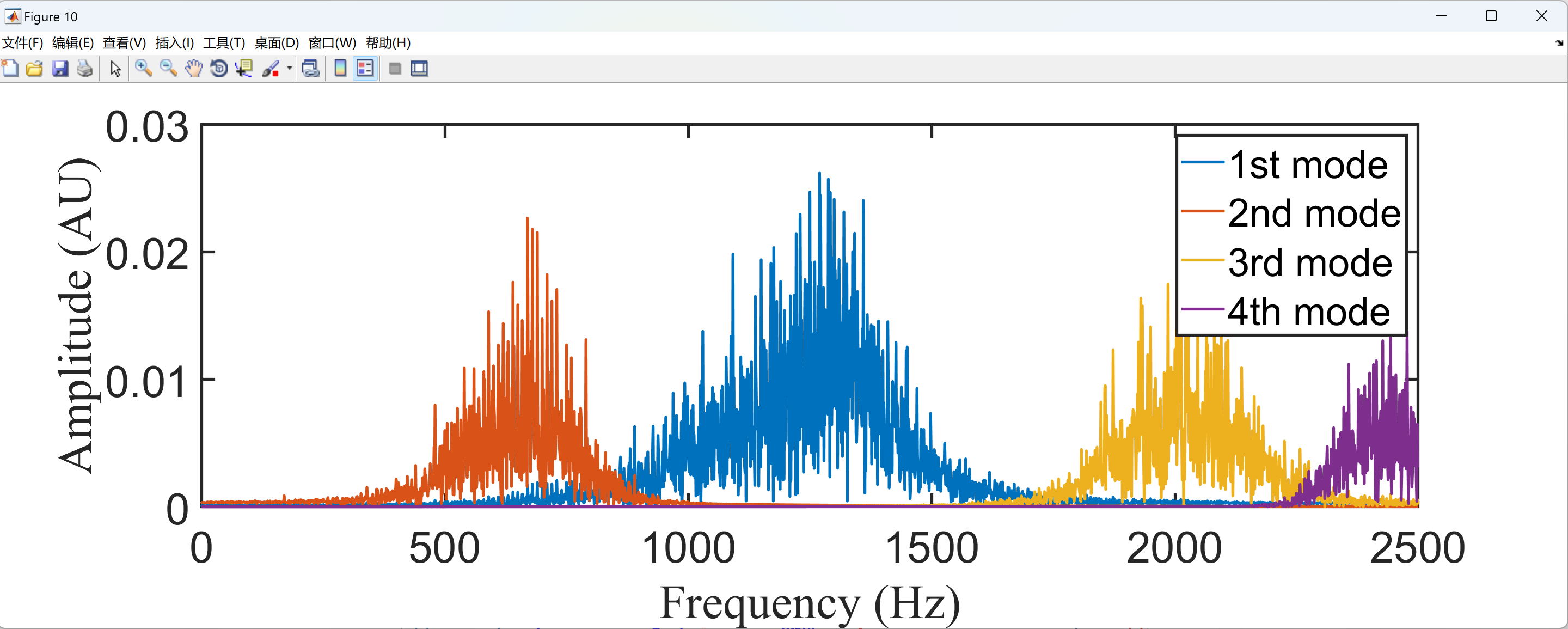
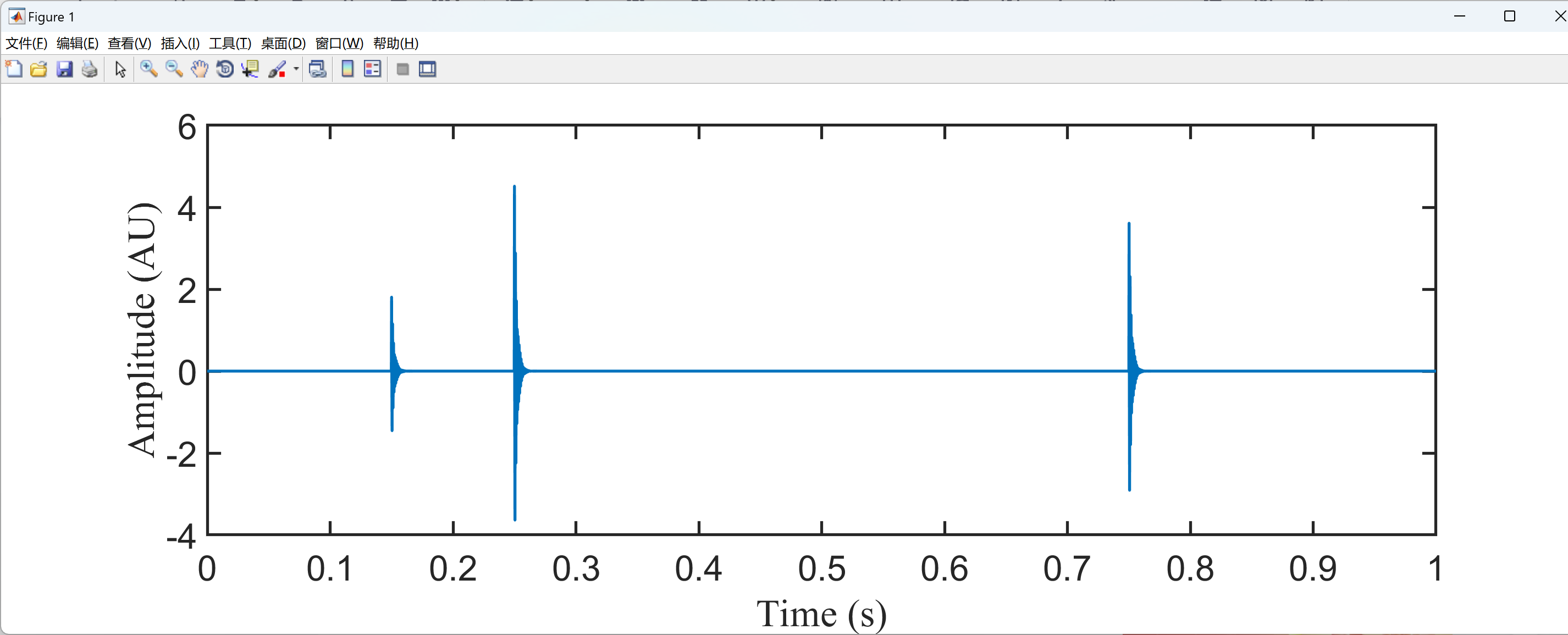
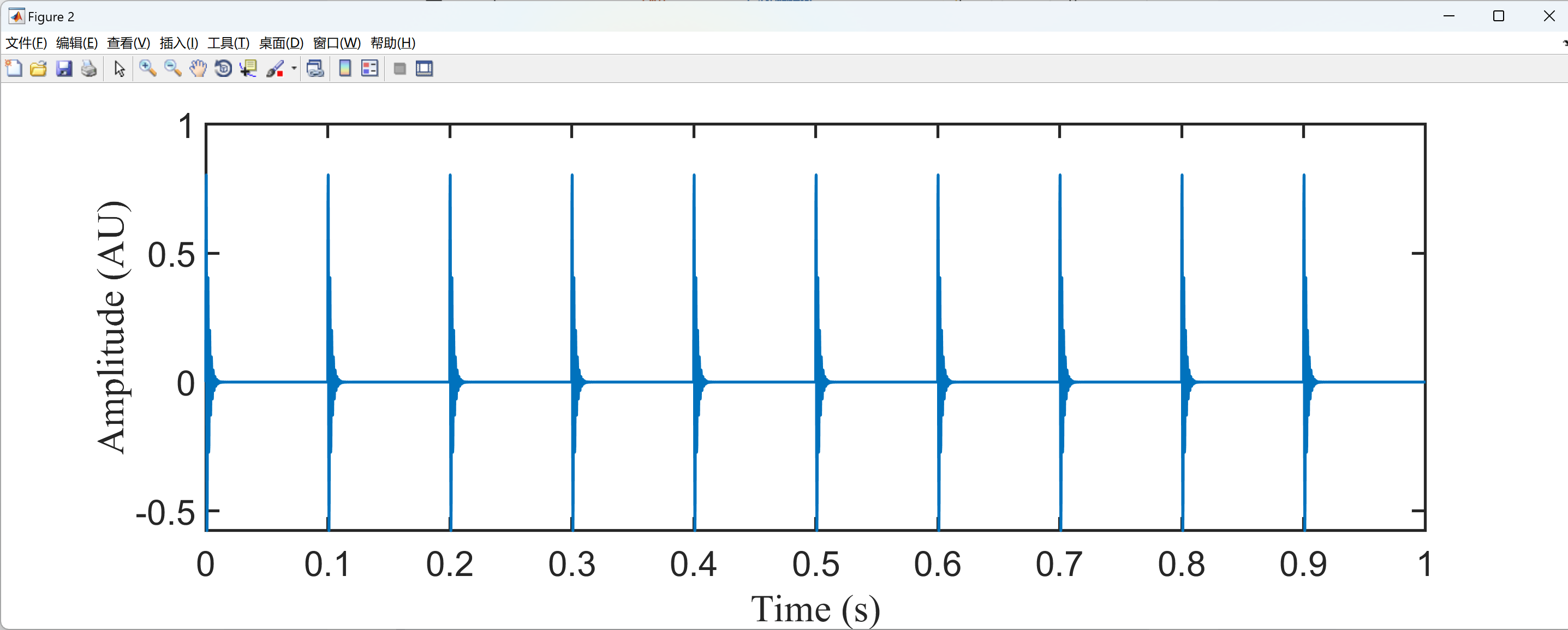
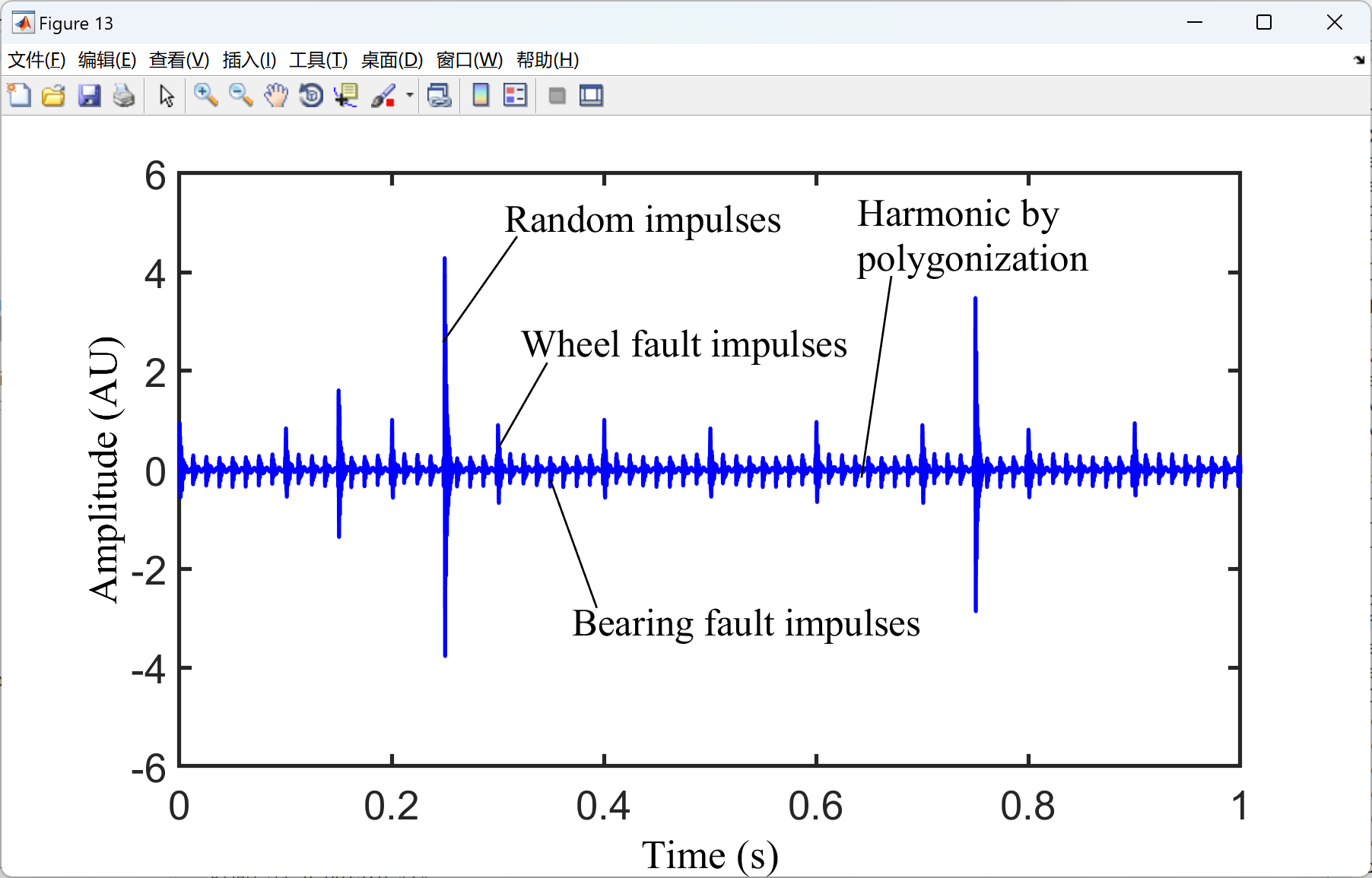
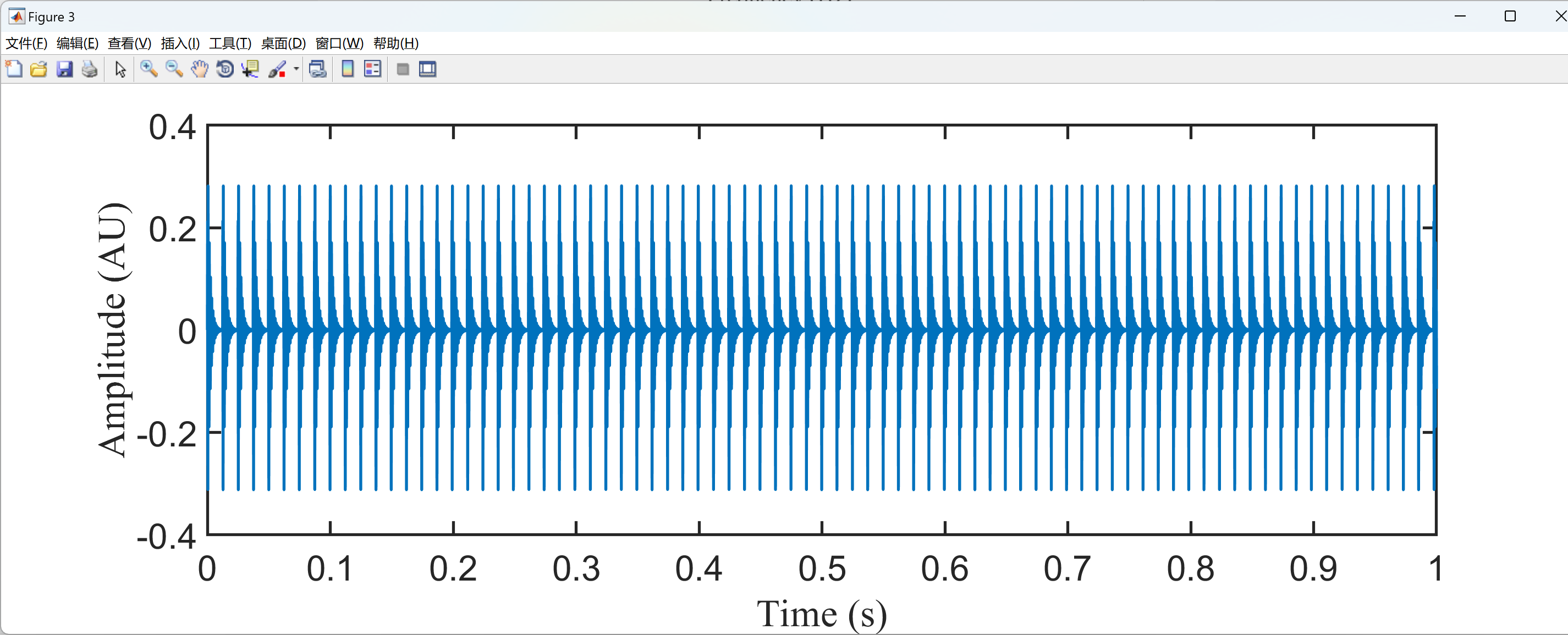
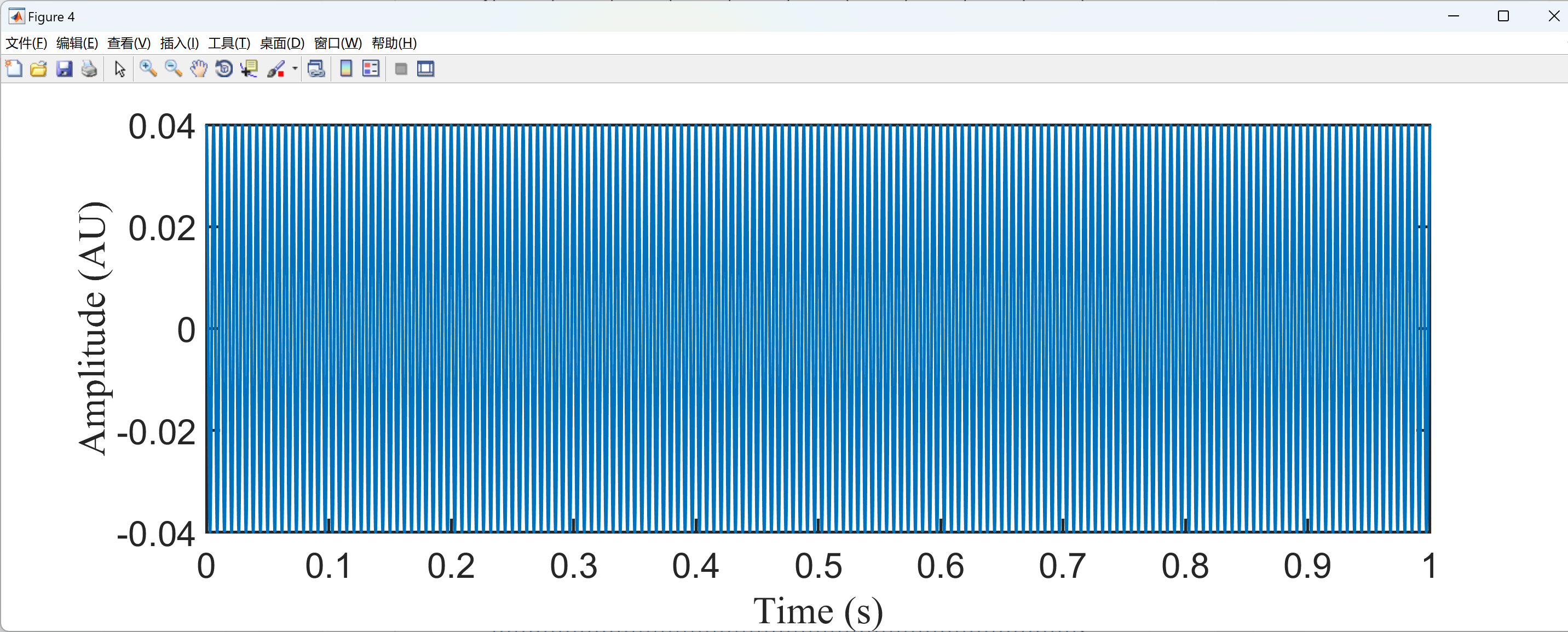
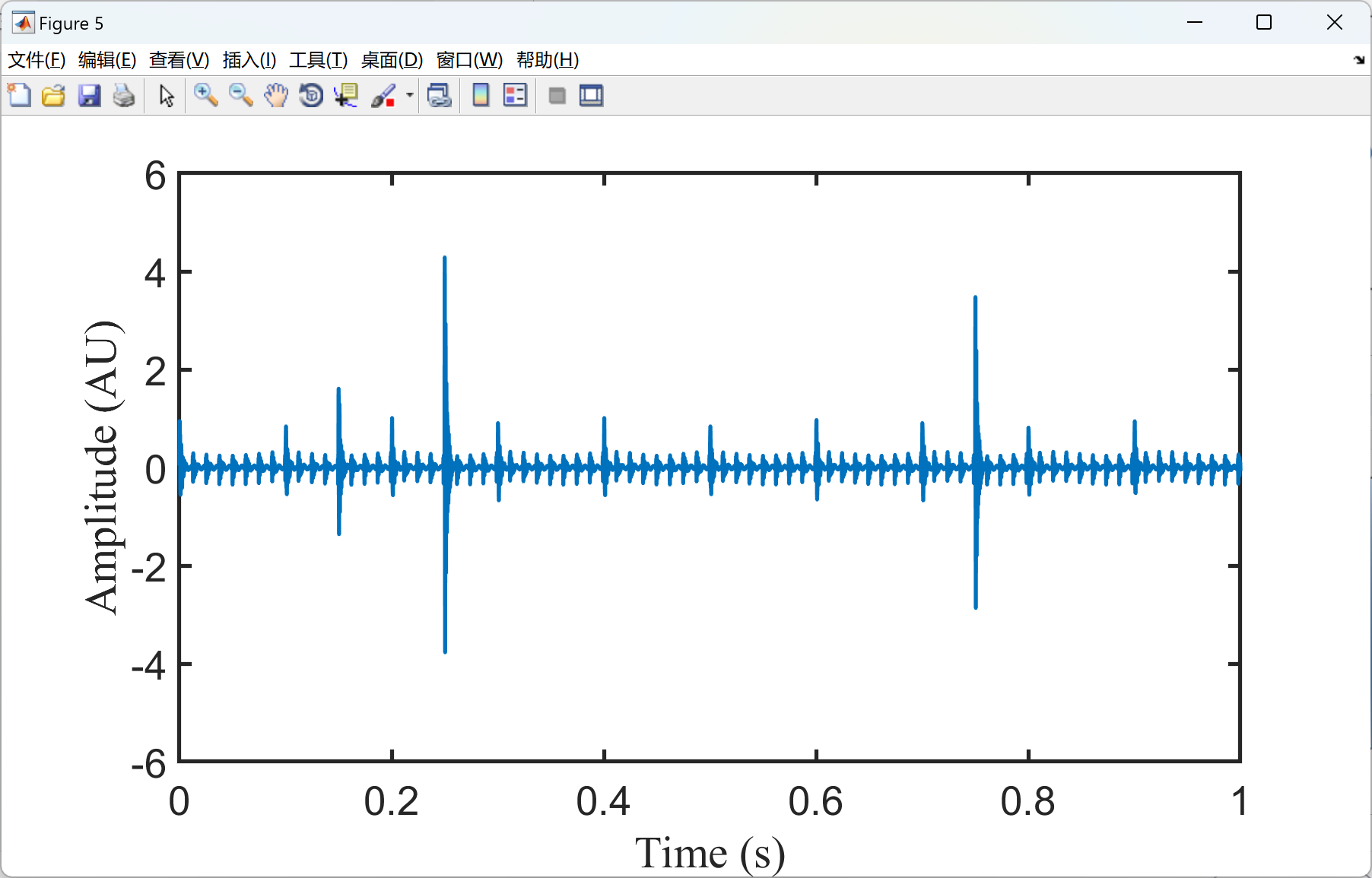
部分代码：

figure
set(gcf,'Position',[20 100 1500 500]);       
set(gcf,'Color','w'); 
plot(t,Sig2,'linewidth',2);
xlabel('Time (s)','FontSize',24,'FontName','Times New Roman');
ylabel('Amplitude (AU)','FontSize',24,'FontName','Times New Roman');
set(gca,'FontSize',24)
set(gca,'linewidth',2);
figure
set(gcf,'Position',[20 100 1500 500]);       
set(gcf,'Color','w'); 
plot(t,Sig1,'linewidth',2);
xlabel('Time (s)','FontSize',24,'FontName','Times New Roman');
ylabel('Amplitude (AU)','FontSize',24,'FontName','Times New Roman');
set(gca,'FontSize',24)
set(gca,'linewidth',2);
figure
set(gcf,'Position',[20 100 1500 500]);       
set(gcf,'Color','w'); 
plot(t,Sig3,'linewidth',2);
xlabel('Time (s)','FontSize',24,'FontName','Times New Roman');
ylabel('Amplitude (AU)','FontSize',24,'FontName','Times New Roman');
set(gca,'FontSize',24)
set(gca,'linewidth',2);
figure
set(gcf,'Position',[20 100 1500 500]);       
set(gcf,'Color','w'); 
plot(t,Sig4,'linewidth',2);
xlabel('Time (s)','FontSize',24,'FontName','Times New Roman');
ylabel('Amplitude (AU)','FontSize',24,'FontName','Times New Roman');
set(gca,'FontSize',24)
set(gca,'linewidth',2);

figure
set(gcf,'Position',[20 100 900 500]);       
set(gcf,'Color','w'); 
plot(t,Sig,'linewidth',2);
xlabel('Time (s)','FontSize',20,'FontName','Times New Roman');
ylabel('Amplitude (AU)','FontSize',20,'FontName','Times New Roman');
set(gca,'FontSize',20)
set(gca,'linewidth',2);
axis([0 1 -6 6])

figure
set(gcf,'Position',[20 100 900 500]);       
set(gcf,'Color','w'); 
plot(t,Sign,'linewidth',2);
xlabel('Time (s)','FontSize',20,'FontName','Times New Roman');
ylabel('Amplitude (AU)','FontSize',20,'FontName','Times New Roman');
set(gca,'FontSize',20)
set(gca,'linewidth',2);
axis([0 1 -6 6])
%%
offset = 0.01;
cutpfreq = 0.0015; 

round(2*length(Sig)*cutpfreq)

tic
[Spec,Weigt,Spec_trend,WeSpec_trend,sortInter] = Spectrendgene(Sign,SampFreq,offset,cutpfreq);
beta = 1e-10;
tol = 1e-7;
ce = 0.3;
[compset IFset IAset] = BAACMD(Sign,SampFreq,beta,tol,ce,offset,cutpfreq);
toc

Freqbin = linspace(0,SampFreq/2,length(Spec));
[peakset,indexp] = findpeaks(-Spec_trend);
figure
set(gcf,'Position',[20 100 900 500]);        
set(gcf,'Color','w'); 
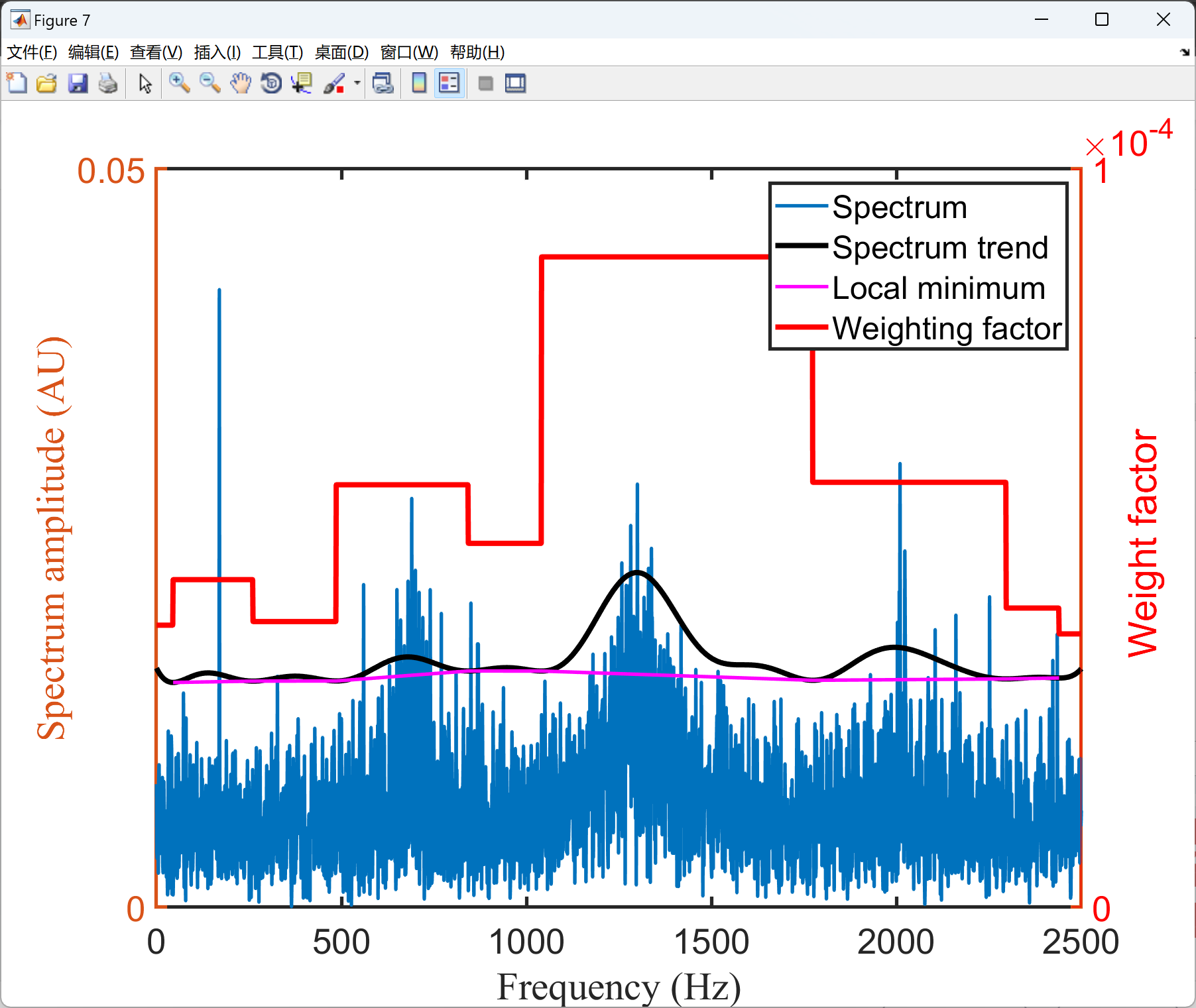
plot(Freqbin,Spec,'linewidth',2);
hold on
plot(Freqbin,Spec_trend,'k','linewidth',3);
ylabel('Amplitude (AU)','FontSize',18,'FontName','Times New Roman');
axis([0 2500 0 1.1*max(Spec)])
hold on     
[AX,H1,H2] =plotyy(Freqbin(indexp),-peakset,Freqbin,Weigt,@plot);% 禄帽脠隆脳酶卤锚脰谩隆垄脥录脧帽戮盲卤煤
set(get(AX(1),'ylabel'),'string', 'Spectrum amplitude (AU)','fontsize',20);
set(get(AX(2),'ylabel'),'string', 'Weight factor ','fontsize',20);
set(AX(2),'Fontsize',20)
set(H1,'linewidth',2);
set(H2,'linewidth',3);
set(H2,'color','r')
set(H1,'color','m')
set(AX(2),'YColor', [1 0 0]);
set(gcf,'color','white')
xlabel('Frequency (Hz)','FontSize',20,'FontName','Times New Roman');
legend('Spectrum','Spectrum trend','Local minimum','Weighting factor')
set(gca,'FontSize',20)
set(gca,'linewidth',2);

figure
set(gcf,'Position',[20 100 900 500]);        
set(gcf,'Color','w'); 
[AX,H1,H2] =plotyy(Freqbin,Spec,Freqbin,WeSpec_trend,@plot);
set(get(AX(1),'ylabel'),'string', 'Spectrum amplitude (AU)','fontsize',20);
set(get(AX(2),'ylabel'),'string', 'Weighted spectrum trend ','fontsize',20);
set(AX(2),'Fontsize',20)
set(H1,'Linestyle','-','linewidth',2);
set(H2,'Linestyle','--','linewidth',3);
set(H1,'color','b')
set(H2,'color','r')
set(AX(2),'YColor', [1 0 0]);
legend('Spectrum','Weighted trend')
set(gcf,'color','white')
xlabel('Frequency (Hz)','FontSize',20,'FontName','Times New Roman');
set(gca,'FontSize',20)
set(gca,'linewidth',2);

Specpset = zeros(size(compset,1),length(Freqbin));

for cpnum = 1:size(compset,1)
Specp1 = (2*abs(fft(compset(cpnum,:)))/length(compset(cpnum,:)));
Specpset(cpnum,:) = Specp1(1:length(Freqbin));
end

figure
set(gcf,'Position',[20 100 1500 500]);       
set(gcf,'Color','w'); 
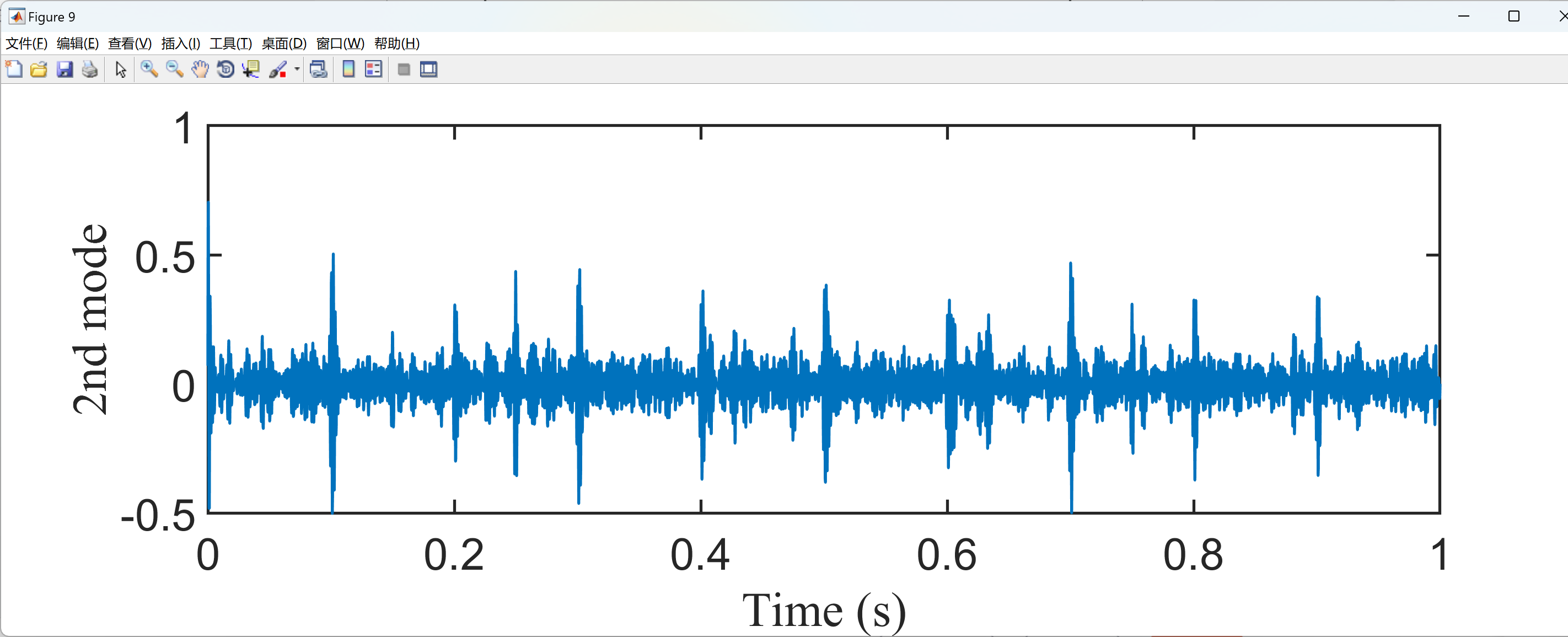
plot(t,compset(2,:),'linewidth',2);
xlabel('Time (s)','FontSize',30,'FontName','Times New Roman');
ylabel('2nd mode','FontSize',30,'FontName','Times New Roman');
set(gca,'FontSize',30)
set(gca,'linewidth',2);
% axis([0 1 -0.4 0.4])

figure
set(gcf,'Position',[20 100 1500 500]);        
set(gcf,'Color','w'); 
plot(Freqbin,Specpset,'linewidth',2);
ylabel('Amplitude (AU)','FontSize',30,'FontName','Times New Roman');
legend('1st mode','2nd mode','3rd mode','4th mode')
set(gcf,'color','white')
xlabel('Frequency (Hz)','FontSize',30,'FontName','Times New Roman');
set(gca,'FontSize',30)
set(gca,'linewidth',2);

[IFcp1 IAcp1]= IFIAextrc(compset(2,:),SampFreq); 
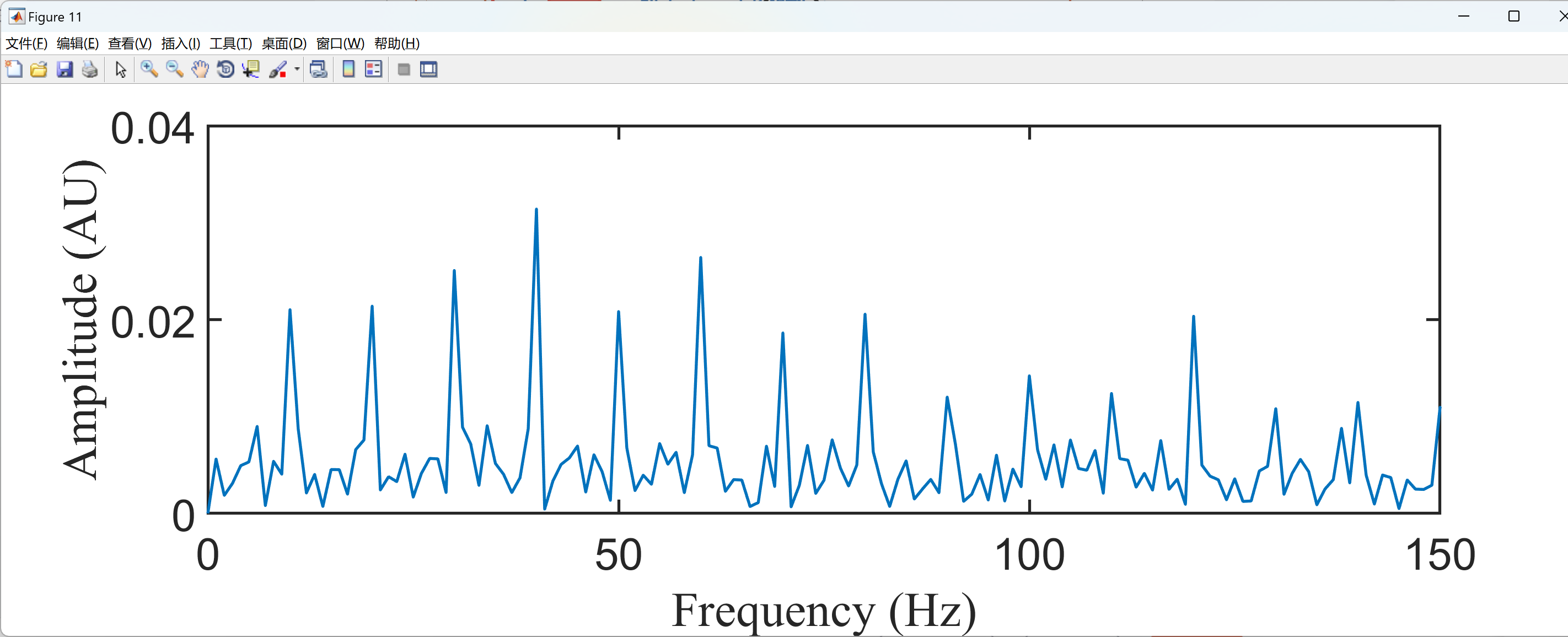
SpeIFcp1 = (2*abs(fft(IAcp1 - mean(IAcp1)))/length(IAcp1)); % envelope spectrum
SpeIFcp1 = SpeIFcp1(1:length(Freqbin));
figure
set(gcf,'Position',[20 100 1500 500]);        
set(gcf,'Color','w'); 
plot(Freqbin,SpeIFcp1,'linewidth',2);
ylabel('Amplitude (AU)','FontSize',30,'FontName','Times New Roman');
set(gcf,'color','white')
xlabel('Frequency (Hz)','FontSize',30,'FontName','Times New Roman');
set(gca,'FontSize',30)
set(gca,'linewidth',2);
axis([0 150 0 0.04])

GN1 = GN_SE(compset(1,:))
GN1 = GN_SE(compset(2,:))
GN1 = GN_SE(compset(3,:))
GN1 = GN_SE(compset(4,:))

🎉3 参考文献

文章中一些内容引自网络，会注明出处或引用为参考文献，难免有未尽之处，如有不妥，请随时联系删除。

[1] Wang X , Tang G , Yan X ,et al.Fault Diagnosis of Wind Turbine Bearing Based on Optimized Adaptive Chirp Mode Decomposition[J].IEEE Sensors Journal, 2021, PP(99):1-1.DOI:10.1109/JSEN.2021.3071164.

[2] Wang H , Chen S , Zhai W .Data-driven adaptive chirp mode decomposition with application to machine fault diagnosis under non-stationary conditions[J].Mechanical Systems and Signal Processing, 2023.DOI:10.1016/j.ymssp.2022.109997.

[3]黄绍伟.自适应调频模式分解在轴承故障诊断中的应用[J].综合智慧能源, 2020, 42(1):54-57.

[4]胡斯念.自适应变分模式分解方法及其在机械故障诊断中的应用[D].武汉科技大学[2024-03-18].

🌈4 Matlab代码实现