机器学习08：生成式对抗网络(GAN)中理论介绍与WGAN②

摘要

        本周深入探讨生成对抗网络（GAN）的训练目标与散度计算，揭示JS散度在分布不重叠时的失效问题。提出Wasserstein距离作为替代方案，其通过推土机类比直观反映分布间转换成本。进而引入WGAN框架，通过1-Lipschitz约束（梯度惩罚与谱归一化）稳定训练。实验证明，Wasserstein距离在生成器进化过程中提供连续梯度信号，有效解决模式坍缩。

Abstract

        This week delves into the training objectives and divergence computation in Generative Adversarial Networks (GANs), highlighting the failure of JS divergence when distributions do not overlap. The Wasserstein distance is proposed as an alternative, intuitively reflecting the transformation cost between distributions via an earth mover analogy. The WGAN framework is introduced, incorporating 1-Lipschitz constraints (gradient penalty and spectral normalization) to stabilize training. Experiments demonstrate that the Wasserstein distance provides continuous gradient signals during generator evolution, effectively resolving mode collapse.

一．GAN训练目标

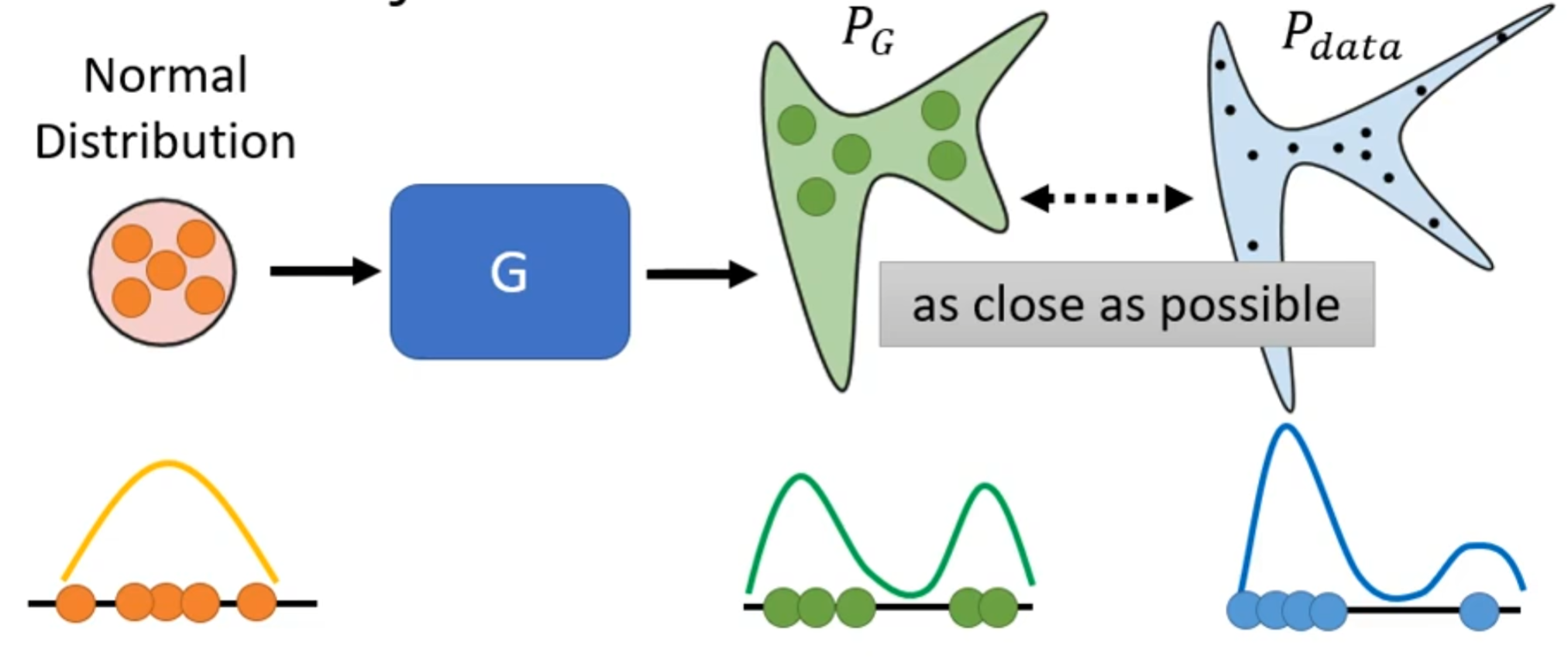
        在训练神经网络中，是要先定一个loss函数，确定完后就要通过梯度下降然后最小化loss函数就结束。而在生成问题中我们想要最小化或者最大化的是使P(G)与P(data)之间的距离越近越好。

        其中P(G)是通过正常分布中抽样然后通过生成器得到的分布，而P(data)则是通过在生成器中输入真实数据得到的分布。就如当输入的如上图中的一维数据通过生成器得到绿色线的分布，而真实的分布如蓝色线分布。

        若表述成式子就如上式子，其中Div是指P(G)与P(data)之间的差距或散度。

        所以我们的训练目标就是去确定一个生成器，该生成器中的参数使得P