【三维数域】码住这篇！K-D树——拿捏近邻搜索与范围查询

在大数据和人工智能时代，如何高效管理和查询多维数据是一项极具挑战性的任务。多维数据广泛存在于诸多领域，如计算机视觉中的特征点匹配、机器学习中的高维样本分类、地理信息系统（GIS）中的地理位置查询以及机器人导航中的路径规划等。

在面对如此复杂的多维数据时，简单的线性扫描方法显然效率低下。为此，K-D树（K-Dimensional Tree）作为一种经典的空间索引结构，通过递归划分空间并组织数据点，提供了高效的最近邻搜索和范围查询能力，被广泛应用于实际问题中。

本文将对K-D树的原理、构建方法、搜索算法及其应用进行全面分析与补充，帮助读者更好地理解这一重要的数据结构。

一、K-D树的定义与原理

K-D树是一种针对多维数据的二叉树数据结构，其核心思想是递归地划分数据空间。通过每次选择一个维度并在该维度上确定划分点，K-D树将数据划分为两个子空间，并通过这种方式有效地组织多维数据。

#基本结构

每个节点表示一个K维空间点，也称为分割点（Splitting Point）。每个节点将当前数据空间划分为两个区域：

左子树：存储当前维度小于划分点的数据。

右子树：存储当前维度大于划分点的数据。

#划分维度的选择

K-D树的划分维度通常按照以下两种方式之一：

• 固定轮转划分：按照维度的顺序依次轮流选择划分维度。例如，第一层选择第一个维度，第二层选择第二个维度，依此类推。
• 最大方差划分：选择具有最大方差的维度作为划分维度，以更均匀地划分数据空间。

这种划分方式使K-D树能够适应多维数据，并在查询时通过分治法快速定位目标区域。

# K-D树的特性

• 平衡性：K-D树的深度与数据点数量呈对数关系（理想情况下），这使得它在空间查询中非常高效。
• 区域划分：每个节点划分出的空间是一个超矩形，随着树的深入，这些超矩形逐渐缩小。

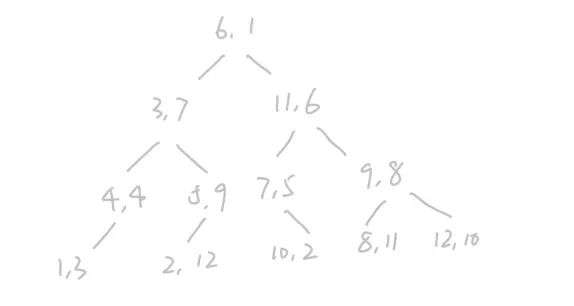
一个 K-D树实例

二、K-D树的构建

构建K-D树的过程是一个递归划分数据的过程，其目标是建立一个分层的二叉树，以便于快速的查询操作。具体步骤如下：

#选择划分维度

在每一层，根据固定轮转规则或最大方差规则选择一个维度进行划分。

例如，对于二维数据，在第一层选择x轴作为划分维度，在第二层选择y轴。

#选择划分点

在选定的划分维度上，将数据点排序，并选择中位数作为划分点。

这种方法可以最大程度地保持树的平衡，避免出现退化成链表的情况。

#递归构建子树

将小于划分点的数据点用于构建左子树，大于划分点的数据点用于构建右子树。重复上述过程，直到所有数据点都被划分，或者达到设定的树深度上限。

#时间复杂度

在理想情况下，K-D树的构建需要对数据进行多次排序，其时间复杂度为 O(nlogn)。

三、K-D树的搜索算法

K-D树最常见的应用包括最近邻搜索和范围查询。以下分别介绍其两种核心搜索算法的工作原理及实现细节。

#最近邻搜索（Nearest Neighbor Search）

最近邻搜索是K-D树最常用的应用之一。其基本思想是从根节点开始，递归地向下搜索，直到找到目标数据点的最近邻点。其基本流程如下：

• 递归搜索叶子节点
  • 从根节点开始，按照目标点在划分维度上的值与当前节点的比较结果，递归地向左子树或右子树搜索，直至抵达叶子节点。
  • 叶子节点是目标点的初始最近邻点。
• 回溯检查
  • 从叶子节点向上回溯，每次检查当前节点是否存在比已知最近邻点更近的点。
  • 如果回溯路径的另一侧子树可能包含比当前最近邻更近的点，则需要递归检查该子树。
• 剪枝优化
  • 如果回溯时发现另一侧子树的MBR距离目标点的最短距离大于当前最近邻点的距离，则剪枝，不再搜索该子树。
  • 时间复杂度：
    平均情况下为 O(log n)。在最坏情况下（例如数据分布不均导致树退化），时间复杂度可能上升至 O(n)。

一个最近邻搜索例子

#范围查询（Range Search）

范围查询用于找到所有位于给定范围内的数据点。其基本流程如下：

• 初始条件

给定一个范围（通常是一个K维超矩形或超球体），从根节点开始搜索。

• 递归搜索

检查当前节点的MBR是否与范围重叠。如果重叠，则继续检查当前节点的子树。

如果当前节点的MBR完全位于范围外，则剪枝，不再搜索其子树。

如果当前节点的数据点在范围内，则将其加入结果集中。

• 输出结果

将所有满足条件的数据点返回。
 

四、K-D树的应用

K-D树因其高效的多维数据管理能力，被广泛应用于以下领域：

• 机器学习

在机器学习中，K-D树广泛用于K近邻算法（K-Nearest Neighbors, KNN），以提高搜索效率。特别是在高维数据空间中，K-D树能够显著减少搜索时间。

• 计算机图形学

在计算机图形学中，K-D树用于加速光线追踪和碰撞检测等操作。通过K-D树，可以快速排除不可能发生碰撞的对象，从而提高计算效率。

• 地理信息系统（GIS）

在地理信息系统中，K-D树用于空间数据的索引和查询，如最近邻搜索和范围查询。通过K-D树，可以高效地查找某个位置附近的地理信息。

• 数据挖掘

K-D树用于多维数据的聚类分析、异常点检测等任务。

K-D树作为一种经典的空间索引结构，因其高效的最近邻搜索和范围查询性能，在计算机视觉、机器学习、GIS等领域有着广泛应用。尽管在高维数据上的性能可能退化，但在中低维场景中，K-D树仍然是空间数据索引的强大工具。通过合理选择划分策略、优化搜索算法，K-D树能够为多维数据的高效管理提供有力支持。

在K-D树之外，还有许多空间索引方法正在发挥着巨大的作用。利用空间索引需要对相关算法有所了解，还需要开发集成，费时费力，使用支持空间索引的框架或平台可获得事半功倍的效果。

Mapmost Studio中用到了多种空间索引方式，矢量地图服务发布使用了R树，三维模型服务发布使用了八叉树，对影像、地形等服务发布使用了四叉树索引，大大提升了加载性能，为用户提供更优质的产品体验，助你通过简单几步操作即可尽享空间索引所带来的性能提升。

Mapmost Studio现已开放在线体验版本，点击此处前往官网体验！