引言:
背包问题始终贯穿着学习算法的全过程,学会并且能够学以致用背包问题尤为重要。
问题描述:
给定n个物品的重量及效益,给定背包的容量。求背包能装的最大效益值,及最大效益值时装入背包的物品编号。
题解:
dp[i][j] i表示考虑前i个物品,j代表当前背包的容量为j。所以如果当前背包不能装下第i个物品,那么dp[i][j]=dp[i-1][j],说明背包容量为j时,考虑前i个物品和考虑前i-1个物品的最大效益值相同(因为当前背包装不下第i个物品),反之,如果当前背包能装下第i个物品,那么就要考虑要不要装入物品i(即装入物品i会不会是背包的最大效益值增加)。如果wealth[i-1]+dp[i-1][j-weight[i-1]]大于dp[i-1][j],说明装入该物品能使背包的效益值变大,则装入该物品;反之则装入该物品不能是背包的效益值变大,所以就不装该物品。由此递推,则dp[dp.size()-1][dp[0].size()-1]就是当前背包容量为dp[0].size()-1,考虑前dp.size()-1个物品的背包最大效益值。
要想知道该物品是否在背包效益值最大的时候装入背包,就要明白上面的递推公式,如果该物品没装入背包,则dp[i][j]=dp[i-1][j],反之,则该物品装入背包。然后再缩小背包容量或物品考虑的规模(即前n个物品,逐步缩小n),直到n=0或背包的剩余容量为0.
代码:
#include<iostream>
#include<vector>
using namespace std;
/*
物品的重量下标从0开始,即weight[0]是编号为1物品的重量
物品的效益下标从0开始,即wealth[0]是编号为1物品的效益
*/
int Max(int a,int b)
{
return a>b?a:b;
}
int max_benefit(vector<vector<int> > &dp,vector<int> weight,vector<int> wealth)//找到最大效益值
{
int i,j;
for(i=0;i<dp.size();i++)
{
for(j=0;j<dp[0].size();j++)
{
if(i==0||j==0)
{
dp[i][j]=0;
cout<<dp[i][j]<<"\t";
continue;
}
int max=0;
if(j<weight[i-1])//容量为j不能装下第i个物品
{
dp[i][j]=dp[i-1][j];
}
else
{
dp[i][j]=Max(dp[i-1][j],wealth[i-1]+dp[i-1][j-weight[i-1]]);
}
cout<<dp[i][j]<<"\t";
}
cout<<endl;
}
return dp[dp.size()-1][dp[0].size()-1];
}
vector<int> Find(vector<vector<int> > dp,vector<int> weight)//找到最大效益值时物品的编号
{
int i,j;
vector<int> res;
i=dp.size()-1;
j=dp[0].size()-1;
while(i>0&&j>0)
{
if(dp[i][j]!=dp[i-1][j])//编号i的物品在背包里
{
res.push_back(i);
j=j-weight[i-1];
i=i-1;
}
else
{
i--;
}
}
return res;
}
int main()
{
int n,i,j,capacity;
cout<<"请输入物品的数量"<<endl;
cin>>n;
cout<<"请输入背包的容量"<<endl;
cin>>capacity;
vector<int> weight(n);
vector<int> wealth(n);
vector<int> res;
cout<<"请输入n个物品的重量"<<endl;
for(i=0;i<n;i++)
{
cin>>weight[i];
}
cout<<"请输入n个物品的价值"<<endl;
for(i=0;i<n;i++)
{
cin>>wealth[i];
}
vector<vector<int> > dp;
for(i=0;i<n+1;i++)
{
vector<int> temp(capacity+1,0);
dp.push_back(temp);
}
cout<<"最大的效益是"<<max_benefit(dp,weight,wealth)<<endl;
res=Find(dp,weight);
cout<<"最大效益值时装入物品的编号"<<endl;
for(i=res.size()-1;i>=0;i--)
{
cout<<res[i]<<"\t";
}
cout<<endl;
return 0;
}
结果展示:
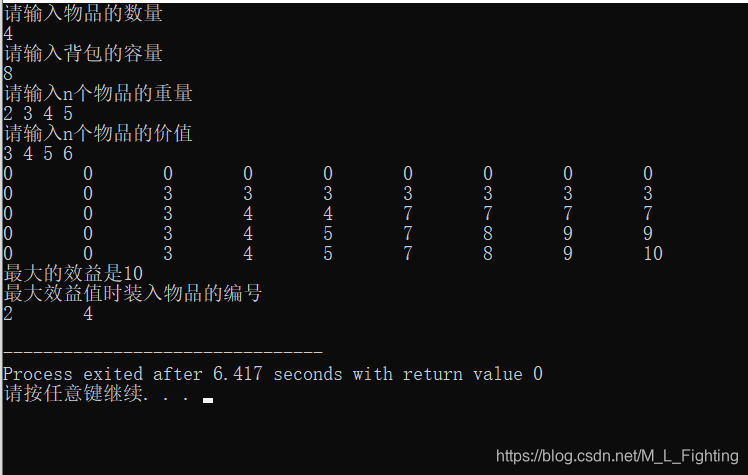
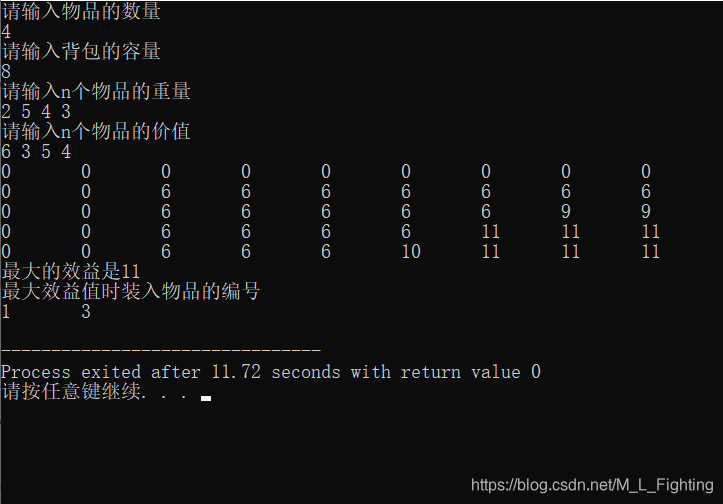






















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








