代码随想录算法训练营第一天| 704. 二分查找、27. 移除元素。

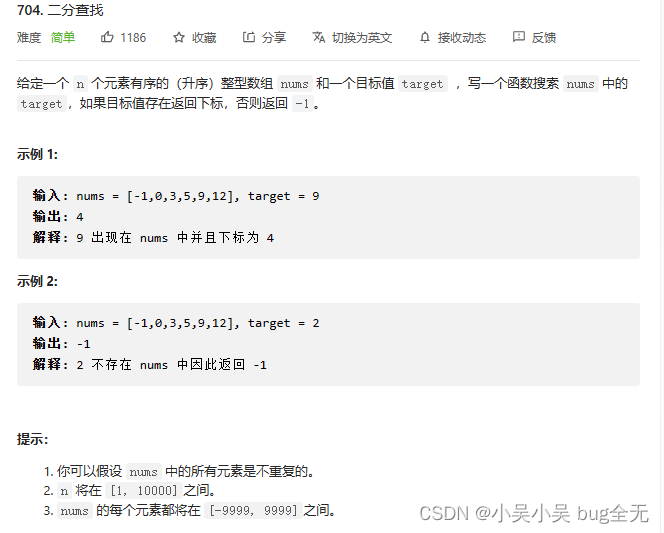
704. 二分查找

题目链接：LeetCode 704. 二分查找 [难度：简单]

【实现代码】

class Solution {
public:
    int search(vector<int>& nums, int target) {
        int left = 0;
        int right = nums.size();//此处为左闭又闭的写法，左闭右开时为nums.size() - 1;
        int mid; 
        while (left < right){//此处为左闭又闭的写法，左闭右开时为left <= right;
            mid = left + (right - left) / 2; // 一定是数组的下标
            if (nums[mid] > target){
                right = mid;//此处为左闭又闭的写法，左闭右开时为right = mid - 1;
            }else if (nums[mid] < target){
                left = mid + 1;//此处为左闭又闭的写法，左闭右开时为left = mid + 1;
            }else{
                return mid;
            }
        }
        return -1;
    }
};

【解题思路】

1. 首先确定数组的边界是左闭又闭（[left, right]），还是左闭右开（[left, right)），这关乎到while循环的循环条件是否可以取到 “=”，我使用左闭右开；
2. 取中间值的下标
3. 判断中间值和目标值的大小。大于目标值，在下半区进行二分查找（left = mid + 1）；小于目标值，在上半区进行二分查找（right= mid），等于目标值直接返回下标。
4. 前提条件：数组是升序的（有序），数组中没有重复值。
5. 关于二分mid溢出问题解答：
   ○ mid = (l + r) / 2时，如果l + r 大于 INT_MAX(C++内，就是int整型的上限)，那么就会产生溢出问题（int类型无法表示该数）
   ○ 所以写成 mid = l + (r - l) / 2或者 mid = l + ((r - l) >> 1) 可以避免溢出问题

【总结】

【第一想法】

1. 确定数组中间下标
2. 将数组中间下标的值与目标值比较，大于目标值，在下半区再进行二分查找；小于目标值，在上半区再进行二分查找，等于目标值直接返回下标。

【存在的问题】

1. 首先知道二分查找的大概思想，但是在确定中间值的下标时忽略了一个大问题，写成了“(left + right) / 2”，理解的是数组的下标，但实际确是相对的中间值；
2. 最开始是想使用vector的迭代器，但是vector一直写成了“verter”，一定要注意单词拼写！

【收获】

1. 熟悉了二分查找的思想
2. 掌握了二分查找两种边界状态的实现代码

27. 移除元素

题目链接：27. 移除元素 [难度：简单]

【实现代码】

class Solution {
public:
    int removeElement(vector<int>& nums, int val) {
        int slowIndex = 0;
        for (int fastIndex = 0; fastIndex < nums.size(); fastIndex++){
            if (val != nums[fastIndex]){
                nums[slowIndex++] = nums[fastIndex];
            }
        }
        return slowIndex;
    }
}

【解题思路】

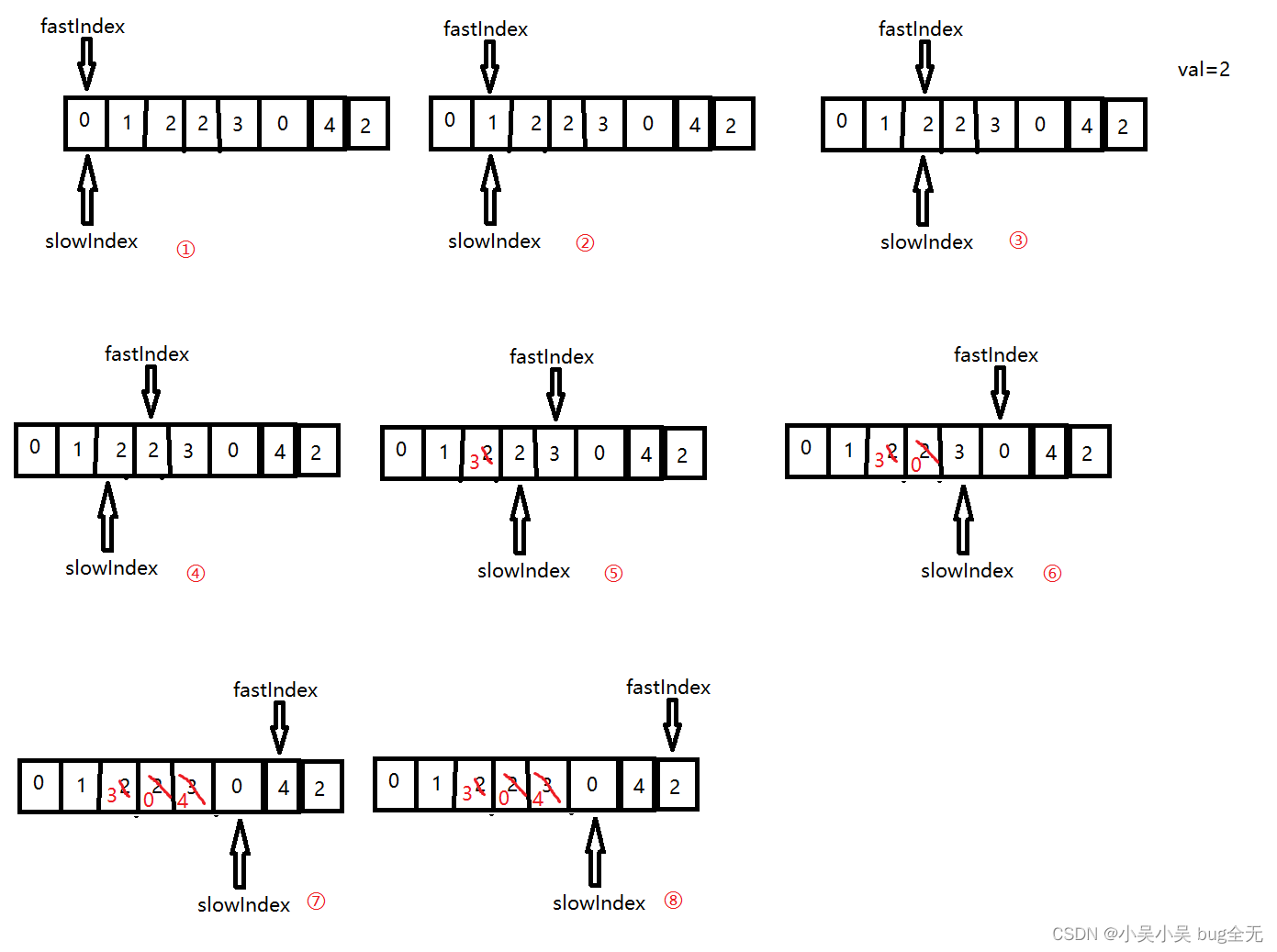
使用快慢指针解决类似题目。本题中由快指针的值覆盖慢指针的值。样例2的双指针示例图如下：

【总结】

【第一想法】

1. 使用两层循环暴力求解，第一层循环找到和val相等的值时，在第二层循环中移到数组末尾。

【存在的问题】

1. 在看到vector时，总想使用迭代器，nums.begin()，nums.end()，给自己增加了难度！
2. 之前做完题后没有进行思考总结，今天上午我刚做了一道牛客的类似的题目（数组元素处理），使用的是快慢指针，下午做到这一题没有一点这样的想法，希望这次能够记住这样的思想。

【收获】

1. 掌握了快慢指针的用法。
2. 在看到数组元素的移动时，尽量先思考能不能使用快慢指针。