二叉树非递归的前中后序遍历

1. LeetCode第144题二叉树非递归前序遍历

二叉树的前序遍历LeetCode链接: link.

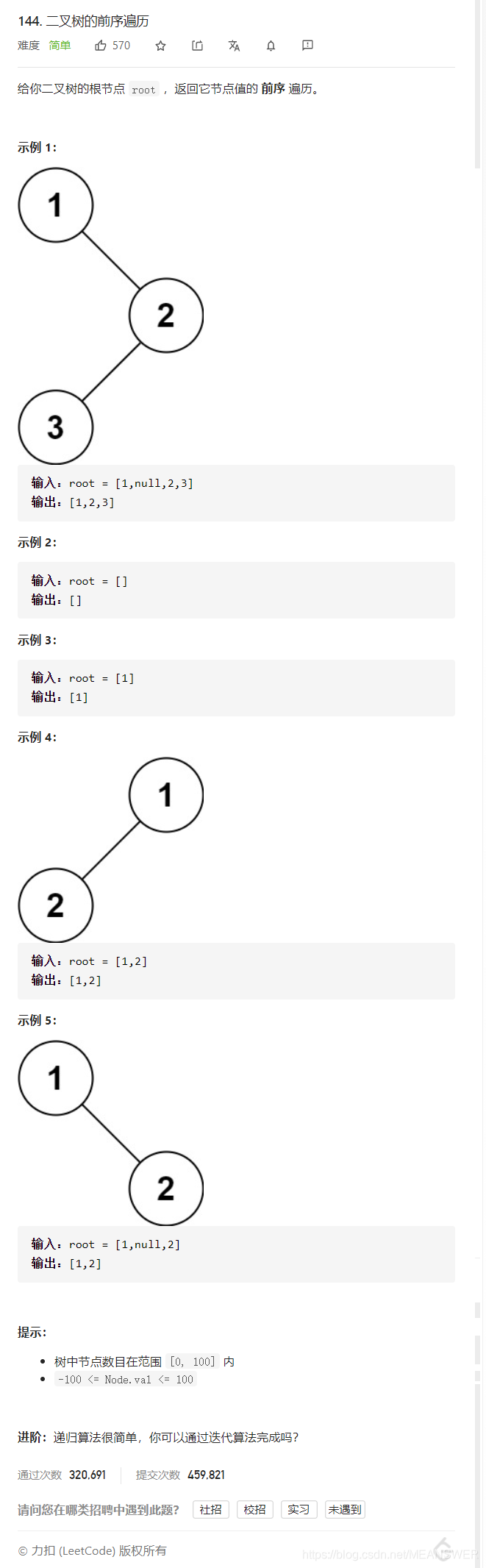
解题思路：前序非递归遍历需要借助栈

1. 如果树为空，直接返回
2. 如果树非空：从根节点位置开始遍历，因为前序遍历规则：根节点、左子树、右子树
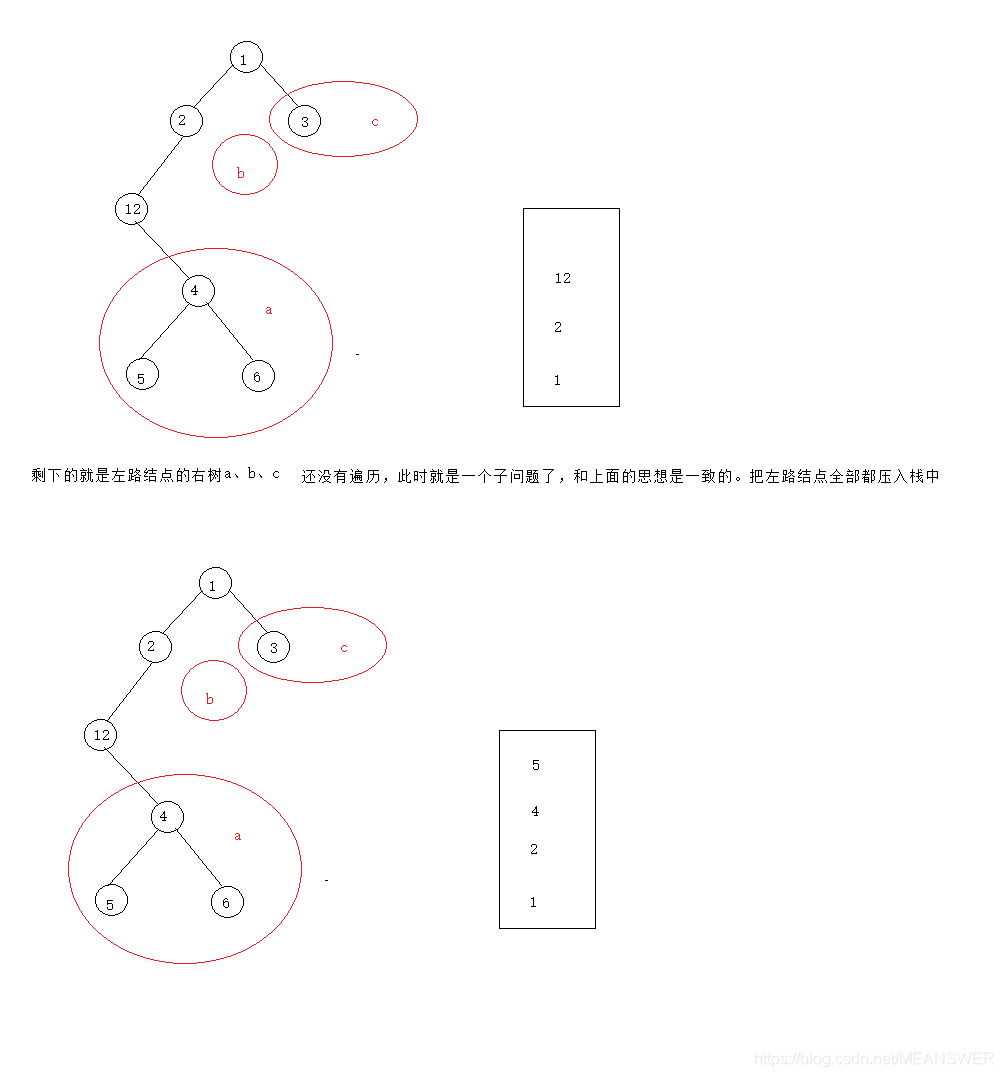
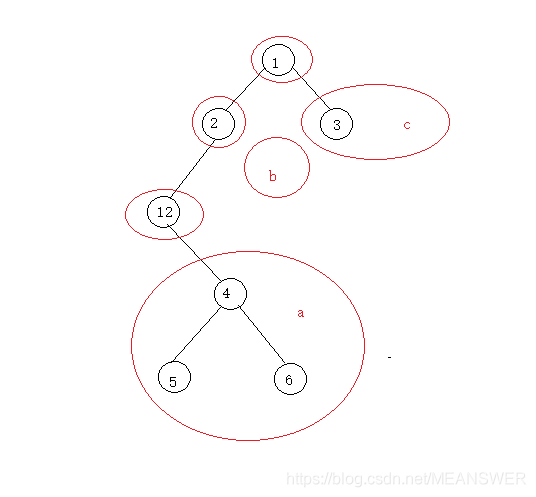
   a. 沿着根节点一直往左走，将所经过路径中的节点依次入栈，并访问。
   b. 取栈顶元素，该元素取到后，其左子树要么为空，要么已经遍历，可以直接遍历该节点，对于该节点，其左子树已经遍历，该节点也已经遍历，剩余其右子树没有遍历，将其当成一棵新的树开始遍历，继续a

class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        stack<TreeNode*> st;
        vector<int> v;
        TreeNode* cur = root;

        //如果你把栈不为空作为条件，那么你刚开始的时候，栈里面就没有内容，岂不是就进不去
        //1.栈里面还有结点，说明还有结点的右子树没有访问
        //2.cur不为空，表示还有树没有访问

        while(cur || !st.empty())
        {
            //1.访问并保存左路结点进栈
            while(cur)
            {
                v.push_back(cur->val);
                st.push(cur);
                cur = cur->left;
            }

            //对于root这棵树，剩下的是左路结点的右子树还没有访问
            //依次把栈里面的拿出来访问
            TreeNode* top = st.top();
            st.pop();

            //子问题走右树
            cur = top->right;
        }
        return v;
    }
};

2. LeetCode第94题二叉树非递归中序遍历

二叉树的中序遍历链接: link.

解题思路：中序非递归遍历需要借助栈

1. 空树，直接返回
2. 如果树非空：从根节点位置开始遍历，但此时根节点不能遍历，因为中序遍历规则：左子树、根节点、右子树
   a. 沿着根节点一直往左走，将所经过路径中的节点依次入栈
   b. 取栈顶元素，该元素取到后，其左子树要么为空，然后就剩下遍历该节点和该节点的右子树，将其右子树当成一棵新的树开始遍历，继续a

class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        stack<TreeNode*> st;
        vector<int> v;
        TreeNode* cur = root;

        while(cur || !st.empty())
        {
            //1.栈存储左路结点
            //2.剩下左路结点和左路结点的右子树没有访问
            while(cur)
            {
                st.push(cur);
                cur = cur->left;
            }

            TreeNode* top = st.top();
            st.pop();
            v.push_back(top->val); //这一步相当于压入根的操作

            //此时这个子问题
            cur = top->right;
        }
        return v;
    }
};

中序遍历和前序遍历的差别就在于往vector里面插入的时间点不同。

3. LeetCode第145题二叉树非递归后续遍历（重要）

二叉树后序遍历链接：链接: link.

解题思路：后序非递归遍历需要借助栈

1. 空树，直接返回
2. 如果树非空：从根节点位置开始遍历，但此时根节点不能遍历，因为后序遍历规则：左子树、右子树、根节点
   a. 沿着根节点一直往左走，将所经过路径中的节点依次入栈
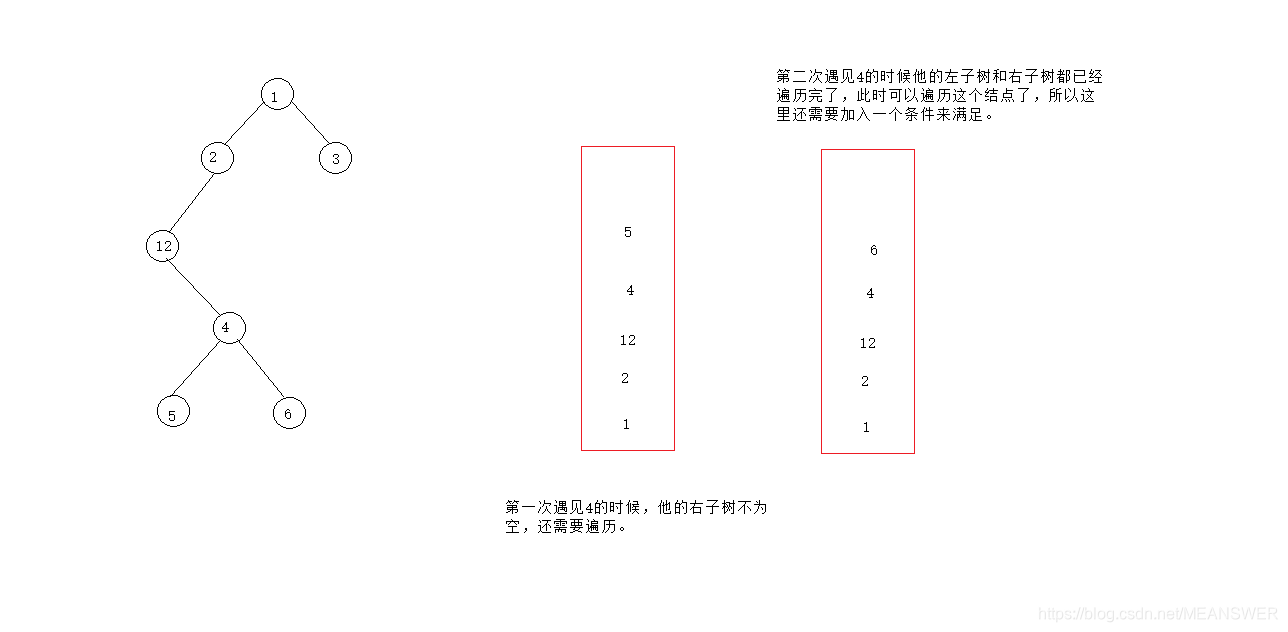
   b. 取栈顶元素，该元素取到后，其左子树要么为空， 但是此时该节点不能遍历，除非其右子树不存在或者其右子树已经遍历，才可以遍历该节点，如果该节点右子树没有遍历，将其右子树作为一棵新的二叉树遍历，继续a
   c. 这道题最难想的就是下图中的结点4，第一次作为栈顶元素的时候，他的右子树是不为空的，所以此时还不能遍历这个结点，第二次4再次作为栈顶的时候，他的右子树已经遍历完了，所以这里还需要再加入一个条件。

class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        stack<TreeNode*> st;
        vector<int> v;
        TreeNode* cur = root;
        TreeNode* prev = nullptr; //因为这颗树里面有可能会有重复的值

        while(cur || !st.empty())
        {
            //1.栈存储左路结点
            while(cur)
            {
                st.push(cur);
                cur = cur->left;
            }

            //2.剩下左路结点和左路结点的右子树没有访问
            TreeNode* top = st.top();
            //这里最大的问题就是你可能会发现卡在了4的位置，第一次发现它的右树不为空，但是第二次你不知道他应该进哪一句代码了
            if(top->right == nullptr || top->right == prev)
            {
                v.push_back(top->val);
                st.pop();
                prev = top;

                cur = nullptr; //保证能取到栈顶的元素
            }
            else
            {
                cur = top->right;
            }
        }
        return v;
    }
};