图的BFS和DFS算法

原创 于 2025-03-26 10:07:11 发布 · 1k 阅读 · 9 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#图论 #算法 #宽度优先 #深度优先 #c语言 #c++ #数据结构

前言

前言

要学习图的广度优先遍历和深度优先遍历算法，首先要了解图的基本概念和图的存储方式。

一、图的基本概念

先来简单回顾一下图的基本概念，用通俗易懂的话来说。

1.图的分类

首先，图这种数据结构，顶点和边分别用V和E表示（无向图的边叫边，有向图的边可以叫边，也可以叫弧--稍微区分一下）。图可以分为有向图和无向图（边是有方向的叫有向图），还可以分为简单图和多重图（多重图是有重复的边，而且存在自己到自己的边，因此我们下面的研究对象是简单图）。

2.顶点的度，入度和出度

无向图的度是指，与当前顶点相连的全部边的个数。有向图的度 = 出度 + 入度。出度是从当前顶点指向其他顶点的边的个数，入度就是从其他顶点指向当前顶点的边的个数。顺便提一句，无向图的全部度之和等于边数的2倍，因为一条边连接两个顶点。有向图的边数 = 全部顶点的入度之和+全部顶点的出度之和，因为一条弧，连接两个顶点。

3.完全图和子图

完全图是什么？无向图的完全图，那就是任意两个顶点之间都有连线。如果是有向图的完全图，那就是任意两个顶点之间都有两条弧，一条从A指向B，一条从B指向A。

多说一句，有向完全图的边个数是：V(V-1) 。无向完全图的边数是：V(V-1)/2 。

子图是什么？子图就是从原来的图中取出来一部分边和顶点，然后形成图。注意了，子图中取出的顶点和边必须严格按照原图的连接关系（即拓扑结构）来保留，但可以选择保留部分边。

子图下面还有个生成子图的概念，生成子图就是包含原图的全部顶点的子图。

4.路径和回路

路径就是从一个顶点到另一个顶点之间经过的顶点序列（不同教材的定义不太一样，但大概意思就是这样）。回路就是从一个顶点出发，经过几个顶点然后回到自己。

距离，就是从一个顶点到另一个顶点的最短路径长度。

简单路径，就是从一个顶点到另一个顶点，中间不经过重复的顶点。

简单回路，就是从一个顶点出发经其他顶点回到自己的过程中不经过重复顶点。

5.连通和强连通

连通是针对无向图的，就是任意两个顶点之间都有路径（注意，意思就是从一个顶点到另一个顶点有路径就行，区别于完全图的任意两个顶点之间有连线）。连通分量，如果无向图里面有好几个部分，各个部分单独连通，那么这些各自单独连通的部分就是各个连通分量。

强连通是针对有向图的，就是任意两个顶点直接都有路径，(和连通不一样的地方是，强连通是从A到B有路径，从B到A也要有路径，也就是要双向奔赴才行）。强连通分量和连通分量差不多，各个部分单独强连通，那么这些各自单独强连通的部分就是各个连通分量。

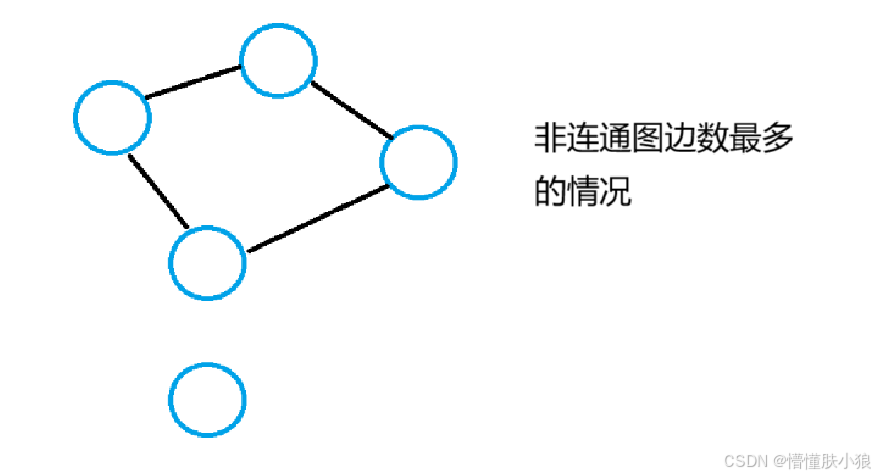
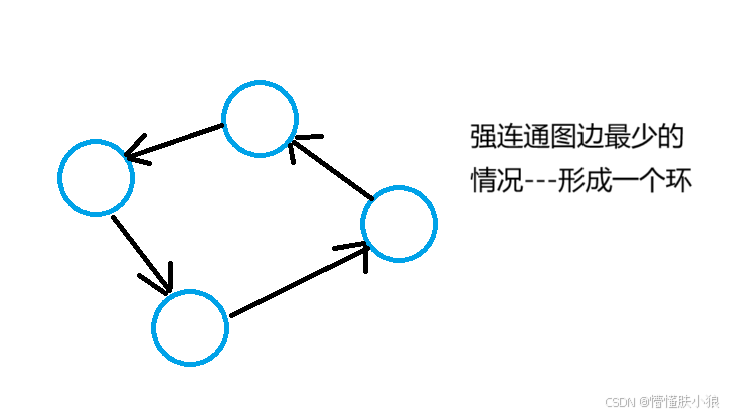
多说一句，连通图，至少要有V-1条边，一个非连通图最多有(V-1)(V-2)/2 条边（因为假设有五个顶点要构成一个连通图，先让四个顶点变为完全图，用组合公式C（下面是V-1，上面是2）计算边，然后剩下一个顶点和其他不连通，那整体就不连通。）。强连通图最少有V条边，形成一个环。

6.生成树和有向树

生成树是啥？其实就是包含一个连通图中的全部顶点的极小连通子图。首先包含全部顶点，然后是连通的，而且极小连通也就是保证连通但是边的数目最少。我们前边已经提到连通图的边数最少就是V-1，所以生成树的边就是V-1个。

生成森林？就是一个非连通图里面的，好几个连通分量，这些连通分量每个都形成一个生成树，这些生成树就构成了一个生成森林。

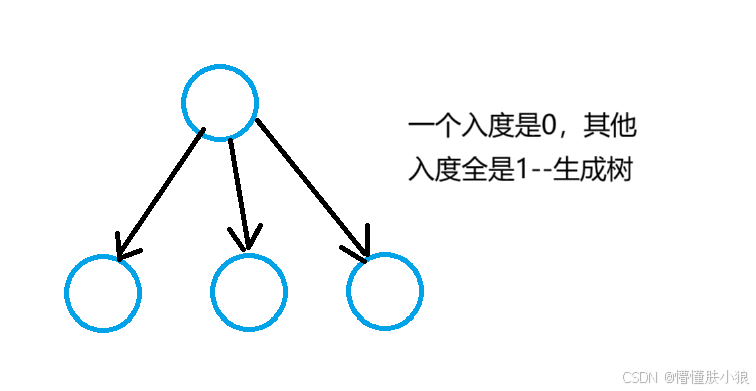
有向树：如果一个有向图，一个顶点的入度是0，其他顶点的入度都是1，那就叫有向树。

二、图的存储方式

1.邻接矩阵存储

简单讲，就是拿一个一维数组存储顶点。拿一个二维数组来存储边。

代码定义如下：(用C语言，掺杂一点C++。下面同)

typedef struct {
    //顶点
    int vertex[MaxVerNum];
    //边
    int edge[MaxVerNum][MaxVerNum];
    //当前的顶点个数和边个数
    int verNUm,edgeNum;
}MGraph;

2.邻接表存储

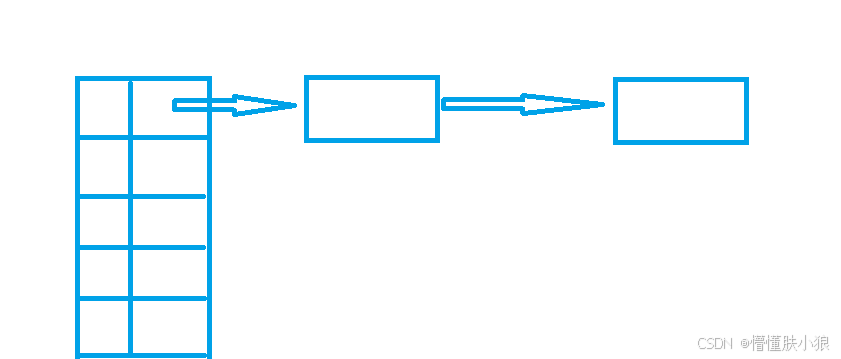
简单讲就是，一个结构体数组存顶点，然后数组中的每个顶点都有一条链表，链表就是指向其他顶点的边。

代码定义如下： 

// 边表结点
typedef struct ArcNode {
    int adjvex;  // 该弧所指向的顶点的位置
    struct ArcNode *nextarc;  // 指向下一条弧的指针
} ArcNode;

// 顶点表结点
typedef struct VNode {
    int data;  // 顶点信息
    ArcNode *firstarc;  // 指向第一条依附该顶点的弧的指针
} VNode, AdjList[MAX_VERTEX_NUM];

// 图的邻接表表示
typedef struct {
    AdjList vertices;
    int vexnum, arcnum;  // 图的当前顶点数和弧数
} ALGraph;

3.十字链表存储

只能存储有向图。

4.邻接多重表存储

只能存储无向图。等后期有空了再补充吧。

三、图的遍历

说了半天废话，终于到正题了。精神!(((o(*ﾟ▽ﾟ*)o)))♡

下面的代码是以邻接矩阵来写的，分析是以邻接矩阵和邻接表来搞的。

1.广度优先遍历BFS

类似于树的层序遍历，但是和树的层序遍历的区别在于，图的广度优先遍历可能会让节点去重复访问一个已经访问过的节点。

因此，设置一个bool类型的标记数组，以索引来表示结点，然后初始化为false，如果结点被访问过了就设置为true。

同时，BFS要使用一个辅助队列，遍历顺序，例如下图：

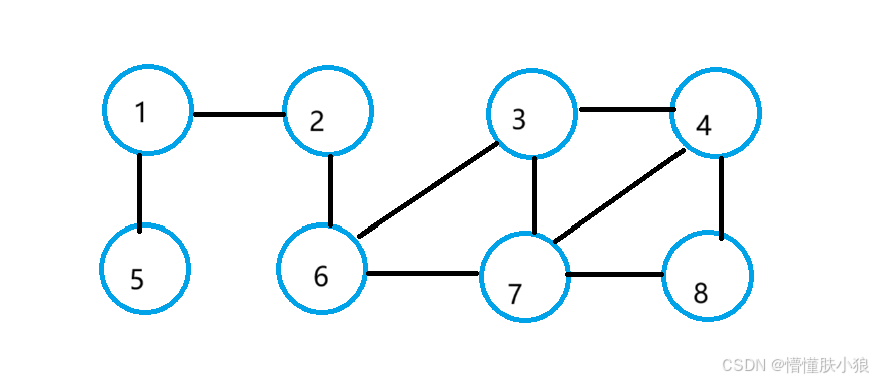
其进队的次序是：

1 - 2 - 5 - 6 - 3 - 7 - 4 - 8。当前顶点出队，就会把其相邻的顶点全部入度。

注意：如果是非连通图，无向图，有几个连通分量，那就要循环几次。如果是有向图，还要看情况访问几次。

空间复杂度：设置辅助队列占用空间，最差情况一次全部进队，O(V)

时间复杂度：邻接矩阵法O(V²)，邻接表法O(V+E)

2.深度优先遍历DFS

DFS类似于树的先根遍历。同样的设置标志数组，防止重复访问。

上图的DFS顺序：假设从1号开始，1-2-6-3-4-7-8-5。从1号开始，深度一直到2,3,4,5,6,7,8，然后这些访问完了之后，栈开始往回，一直到1号，然后找到5号。

如果是非连通图，无向图，有几个连通分量，那就要循环几次。如果是有向图，还要看情况访问几次。

空间复杂度：使用递归算法，栈的深度最大是一次全部进栈，也就是O(V)

时间复杂度：邻接矩阵法O(V²)，邻接表法O(V+E)

3.BFS和DFS代码(邻接矩阵实现)

如图，先建立一个图如上所示，然后广度优先，深度优先分别遍历。

可以手动模拟一下以各个点为起点的遍历顺序和代码是否一致。

#include <iostream>
/**
 * 图的邻接矩阵存储方式
 * 图的基本操作，包含 查找其第一个相邻结点，查找下一个相邻结点
 * BFS 和 DFS
 */

#define MaxVerNum 8
#define INFINITY 1000

// 邻接矩阵存储结构
typedef struct {
    //顶点
    int vertex[MaxVerNum];
    //边
    int edge[MaxVerNum][MaxVerNum];
    //当前的顶点个数和边个数
    int verNUm,edgeNum;
}MGraph;

//邻接矩阵创建一个图
void createMGraph(MGraph *&MG){
    int a[8] = {1,2,3,4,5,6,7,8};
    //将上面数组中的值，建立一个图
    //先设置顶点
    for(int i=0;i<MaxVerNum;i++){
        MG->vertex[i] = a[i];
        MG->verNUm++;
    }
    //初始化全部边的权值为INFINITY
    for(int i=0;i<MaxVerNum;i++){
        for(int j=0;j<MaxVerNum;j++){
            MG->edge[i][j] = INFINITY;
            MG->edgeNum++;
        }
    }
    //设置相连顶点的边,1可以换位其他值表示权值
    MG->edge[0][1] = 1;MG->edge[1][0] = 1;
    MG->edge[7][6] = 1;MG->edge[6][7] = 1;
    MG->edge[0][4] = 1;MG->edge[4][0] = 1;
    MG->edge[1][5] = 1;MG->edge[5][1] = 1;
    MG->edge[5][2] = 1;MG->edge[2][5] = 1;
    MG->edge[2][6] = 1;MG->edge[6][2] = 1;
    MG->edge[5][6] = 1;MG->edge[6][5] = 1;
    MG->edge[2][3] = 1;MG->edge[3][2] = 1;
    MG->edge[3][6] = 1;MG->edge[6][3] = 1;
    MG->edge[7][3] = 1;MG->edge[3][7] = 1;
}

//广度优先遍历
//设置队列
typedef struct Queue{
    int *array;
    int front,rear;
}Queue;

//入队，出队操作
void EnQueue(Queue *&q,int value){
    if(q->rear == MaxVerNum-1){
        return ;
    }
    q->array[q->rear++] = value;
}
int DeQueue(Queue *&q){
    if(q->rear == q->front){
        return -1;
    }
    int value = q->array[q->front++];
    return value;
}

void visit(int vertex){
    printf("%2d",vertex);
}
//查询某个值的索引
int search(MGraph *MG,int value){
    for(int i=0;i<MaxVerNum;i++){
        if(MG->vertex[i] == value){
            return i;
        }
    }
    return -1;
}

//找到当前节点的第一个相连结点
int firstNeighbor(MGraph *MG,int vertex){
    //找不到返回-1
    int vertexReturn = -1;
    for(int i=0;i<MaxVerNum;i++){
        if(MG->edge[vertex][i]!=INFINITY){
            vertexReturn = i;
            break;
        }
    }
    return vertexReturn;
}

//找到与当前节点相连的第一个节点除外的下一个结点,vertex1是vertex0的一个邻接点，
//返回除vertex1外的下一个邻接点号
int nextNeighbor(MGraph *MG, int vertex0, int vertex1) {
    int vertexReturn = -1;
    for(int i=0;i<MaxVerNum;i++){
        if(MG->edge[vertex0][i]!=INFINITY && i>vertex1){
            vertexReturn = i;
            break;
        }
    }
    return vertexReturn;
}

//vertexIndex 是索引，比如从第一个元素开始，那么传来的就是0
void BFS(MGraph *MG,int vertexIndex,bool verFlag[]){
    //初始化队列
    Queue *q = (Queue*) calloc(1,sizeof(Queue));
    q->array = (int *) calloc(MaxVerNum,sizeof(int));
    //当前节点入队,比如当前是以1开始的
    visit(MG->vertex[vertexIndex]);
    verFlag[vertexIndex] = true;
    EnQueue(q,MG->vertex[vertexIndex]);
    //当队列不为空
    while(q->rear != q->front){
        //这里由于建立的图特殊，出队元素减一就是他的索引，如果不是，就要查询这个顶点的索引
        int key = DeQueue(q);
        //遍历全部当前节点相邻的结点
        for(int w=firstNeighbor(MG,key-1);w>=0;w= nextNeighbor(MG, key-1, w)){
            if(!verFlag[w]){
                EnQueue(q,MG->vertex[w]);
                visit(MG->vertex[w]);
                verFlag[w] = true;
            }
        }
    }
}

//设置标志数组，防止多次访问同一个节点。循环访问为了防止非连通图
void BFS_Traverse(MGraph *MG){
    bool verFlag[MaxVerNum];
    //注意，这里的0表示图中的1
    for(int i=0;i<MaxVerNum;i++){
        verFlag[i] = false;
    }
    printf("BFS--------!!!\n");
    for(int i=0;i<MaxVerNum;i++){
        if(!verFlag[i]){
            BFS(MG,i,verFlag);
        }
    }
    printf("\n");
}

//图的深度递归遍历(index表示从第几个元素开始遍历，index是该元素的索引位置)
void DFS(MGraph *MG,int index,bool verFlag[]){
    //先访问当前节点
    visit(MG->vertex[index]);
    verFlag[index] = true;
    for(int w=firstNeighbor(MG,index);w>=0;w=nextNeighbor(MG,index,w)){
        if(!verFlag[w]){
            DFS(MG,w,verFlag);
        }
    }
}
void DFS_Traverse(MGraph *MG){
    bool verFlag[MaxVerNum];
    //注意，这里的0表示图中的1
    for(int i=0;i<MaxVerNum;i++){
        verFlag[i] = false;
    }
    printf("DFS--------!!!\n");
    for(int i=0;i<MaxVerNum;i++){
        if(!verFlag[i]){
            DFS(MG,i,verFlag);
        }
    }
    printf("\n");
}

int main() {
    MGraph *MG = (MGraph*) calloc(1,sizeof(MGraph));
    createMGraph(MG);
    BFS_Traverse(MG);
    DFS_Traverse(MG);
    return 0;
}

总结

以上就是今天要讲的内容，本文简单介绍了图的概念，存储，遍历方法，还有许多补全的余地，后续有空了慢慢补吧。

评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值