算法分析笔记

计算问题（computational problem）是对于输入输出的一组规定。例如 sorting 问题

Input: Array a[1...n]
Output: Permutation a'[1...n] s.t. a'[i] <= a'[j] for all 1 <= i < j <= n 

对于一个问题的合法输入称为问题实例（problem instance）。如果一个计算过程（computational procedure）可以把任意的问题实例映射到期望输出，就称之为一个正确的算法（algorithom）。

算法分析

算法分析可以帮助我们比较不同的算法。

正确性（Correctness）

一个正确的算法，应该对所有合法输入，在有限时间内输出正确结果。

An algorithm is correct if when given a valid input it computes for a finite amount of time and produces the right answer.

所以在分析算法正确性之前，应该明确指出，对于每个输入，什么样的输出才是正确的。对于循环，通常使用数学归纳法证明。

复杂度

时间复杂度（Time Complexity）通常可以分为三类

• worst-case (usually) maximum time
• average-case (sometimes) expected time, with assumption of statistical distribution of inputs
• best-case (bogus) cheat with a slow algorithm that works fast on some input.

空间复杂度（Space Complexity）通常包括以下部分

• 指令空间
• 数据空间（不包括输入数据）
• 栈空间

简洁性（Simplicity）

简洁性在算法分析、代码实现、纠错过程中非常关键。

最优性（Optimality）

如果没有一个算法比当前算法的时间复杂度更低，则当前算法具有最优性。通常，我们可以构造一个时间复杂度的下界，然后证明当前算法达到了下界，从而证明最优性。

伪代码（Pseudo Code）

在 LaTex 中插入伪代码时需要使用宏包

\usepackage[ruled, linesnumbered]{algorithm2e}

宏包中最常用的环境是

\begin{algorithm}
\caption{algorithm name}
\KwIn{input values}
\KwOut{output values}
	procedures\;
\end{algorithm}

这一环境属于浮动体，因此可以像 figure 环境一样使用 label 等命令。环境内部预定义了一些命令

\If(then comment){condition}{then clause\;}
\BlankLine
\eIf(then comment){condition}{then clause\;}(else comment){else clause\;}
\BlankLine
\For(for comment){condition}{For-loop body\;}
\BlankLine
\ForEach(foreach comment){condition}{ForEach-loop body\;}
\BlankLine
\ForAll(forall comment){condition}{ForAll-loop body\;}
\BlankLine
\While(while comment){condition}{While-loop body\;}
\BlankLine
\Repeat(repeat comment){condition}{Repeat-loop body\;}(until comment)	
\BlankLine
\Return{return values\;}

注释命令可以缺省

\tcc{c style comment}
\If(\tcc*[f]{in block comment}){condition}{then clause\;}
\tcp{cpp style comment}
\If(\tcp*[h]{in block comment}){condition}{then clause\;}

如果需要实现更为复杂的分支结构，可以使用 if-elseif-else 结构

\uIf(\tcc*[f]{if comment}){condition}{
	if clause\;
} \uElseIf(\tcc*[f]{else if comment}){condition}{
	else if clause\;
} \Else(\tcc*[f]{else comment}){
	else clause\;
}

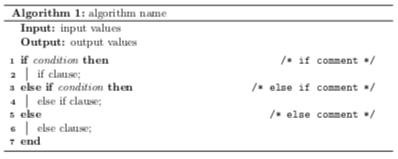
或 switch-case 语句

\Switch(\tcc*[f]{switch comment}){condition}{
	\uCase(\tcc*[f]{case comment}){case description}{case block\;}
	\Other(\tcc*[f]{other comment}){otherwise block\;}
}

要定义、声明并调用一个函数

\begin{function}
\caption{function name (argument1, argument2)}
\KwData{input arguments}
\KwResult{return values}
	function body\;
\end{function}

\begin{algorithm}
\caption{algorithm name}
\KwIn{input values}
\KwOut{output values}
	\SetKwFunction{func}{fn}
	\func{arg1, arg2}\;
\end{algorithm}

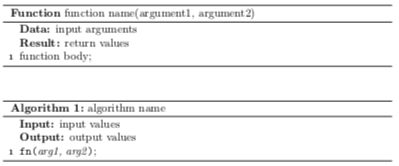
可以针对某一行进行 label 和 ref 操作

procedures\; \label{algorithm:linelabel:procedures}
goto line \ref{algorithm:linelabel:procedures}\;

分治（Divide and Conquer）

分治一般有以下步骤

1. 划分（divide the problem into subproblems）
2. 解决（conquer recursively solve the subproblems）
3. 合并（combine subproblem solutions）

假设我们把原问题分为 $a$ 个子问题，每个子问题的输入大小为 $n/b$ ，划分和合并过程的时间复杂度为 $f(n)$ ，那么分治算法的时间复杂度可以表示为

$$T(n)=aT(n/b)+f(n)$$

递推式（Recurrences）

递推式描述了一种函数，他的值依赖于更小输入尺度下的函数值。

A recurrence is an equality or inequality equation, which dipict a function with function values on smaller input scales.

例如，归并排序的递推式为

$$T(n)=\{\begin{array}{ll}\Theta (1),& n=1\\ 2T(n/2)+\Theta (n),& n>1\end{array}$$

当 $n>1$ 时，我们需要递推地解决子问题，直到 $n=1$

• recursive case the $n>1$ case
• base case the $n=0$ case

递归树（Recursion Tree）

递归树可以用于求解递推式，但这种方法得出的结果往往并不可靠。对于上述例子

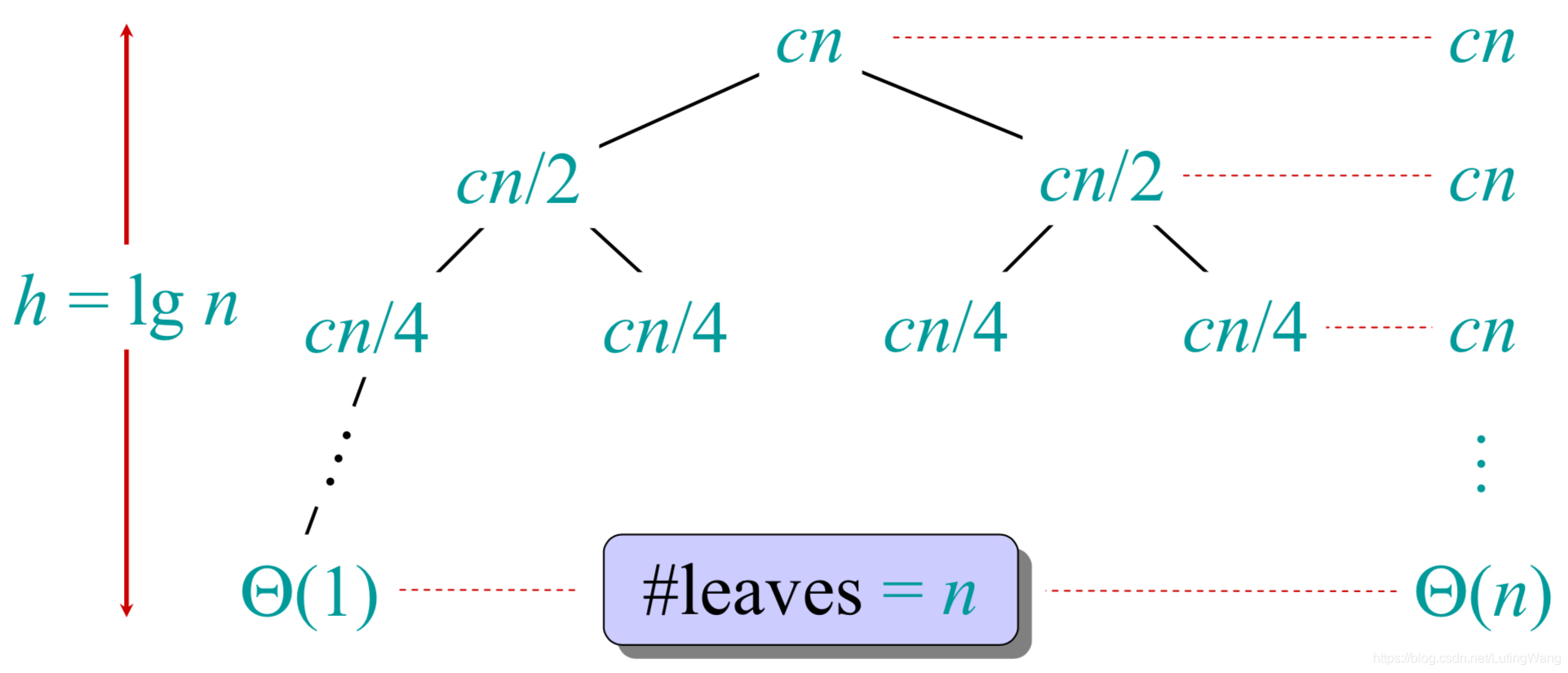
可以求出
$$T(n)=cn\log n+\Theta (n)=O(n\log n)$$

数学归纳法（Induction）

如果我们可以猜出解的形式，就可以使用数学归纳法证明。假设 $T(k)\le ck\log k,\forall k\in (0,n)$ 对某个 $c>0$ 成立，那么只要 $c\ge 1$ ，就会有

$$\begin{array}{rcl}T(n)& \le & 2c\frac{n}{2}\log \frac{n}{2}+n\\ & =& cn\log n-(c-1)n\\ & \le & cn\log n\end{array}$$

值得注意的是，我们需要导出与归纳假设（induction hypothesis）完全相同的结论，而不是简单的

$$cn\log n-(c-1)n=O(n\log n)$$

我们还需要验证基本情况（base cases）。在这个具体问题中，我们无法证明

$$T(1)=1\le c\log 1=0$$

但是我们可以证明，对于 $\forall c\ge 2$ ，有

$$\begin{gathered} T(2)=2T(1)+2=4\le 2c\log 2 \\ T(3)=2T(1)+3=5\le 3c\log 3 \end{gathered}$$

因此，我们证明了

$$\forall c\ge 2,n\ge 2,T(n)\le cn\log n$$

等价于

$$T(n)=O(n\log n)$$

强化归纳假设（Strengthen I.H.）

考虑递推式

$$T(n)=2T(n/2)+1$$

我们猜测解的形式是 $T(n)=O(n)$ 。如果归纳假设是 $T(k)\le ck$ ，会得到

$$T(n)=2c\frac{n}{2}+1\nleqq cn$$

但是如果我们减去一个低阶项 $T(k)\le ck-d$ ，那么只要 $d\ge 1$ ，就有

$$T(n)=2c\frac{n}{2}-2d+1\le cn-d$$

变量替换（Variable Substitution）

考虑递推式

$$T(n)=2T(\sqrt{n})+\log n$$

使用 $m=\log n$ 和 $S(m)=T(2^m)$ 进行替换可以得到

$$\begin{array}{rcl}T(2^m)& =& 2T(2^{m/2})+m\\ S(m)& =& 2S(m/2)+m\end{array}$$

因此

$$\begin{array}{rcl}S(m)& =& O(m\log m)\\ T(n)& =& O(\log n\log (\log n))\end{array}$$

主方法（Master Method）

主方法对以下形式的递推式有效

$$T(n)=aT(n/b)+f(n)$$

其中 $a\ge 1$ ， $b>1$ ，而且 $f$ 是渐进正函数（asymptotically positive）

$$T(n)=\{\begin{array}{ll}\Theta (n^{{\log }_{b}a}),& \exists ϵ>0\text{ s.t. }f(n)=O(n^{{\log }_{b}a-ϵ})\\ \Theta (n^{{\log }_{b}a}{\log }^{k+1}n),& \exists k\ge 0\text{ s.t. }f(n)=\Theta (n^{{\log }_{b}a}{\log }^{k}n)\\ \Theta (f(n)),& \exists ϵ>0\text{ s.t. }f(n)=\Omega (n^{{\log }_{b}a+ϵ})\end{array}$$

需要注意的是，在使用第三种情况时 $f(n)$ 需要满足

$$\exists c<1,\exists N\text{ s.t. }\forall n>N,af(n/b)\le cf(n)$$

以上题为例

$$\begin{array}{rl}\because & a=b=2\\ & \\ & f(n)=n\\ & \\ \therefore & T(n)=O(n\log n)\end{array}$$

二叉搜索（Binary Search）

To find an element in a sorted array

• divide check middle element
• conquer recursively search $1$ subarray
• combine trivial

$$\begin{array}{rcl}T(n)& =& T(n/2)+\Theta (1)\\ & =& \Theta (\log n)\end{array}$$

矩阵乘法（Matrix Multiplication）

Based on the definition, we have an algorithm
$$T(n)=\Theta (n^3)$$

Adopting the D&C idea, we think of dividing a $n\times n$ matrix into $2\times 2$ matrix of $(n/2)\times (n/2)$ sub matrices
$$\begin{array}{rcl}\left[\begin{array}{cc}r& s\\ t& u\end{array}\right]& =& \left[\begin{array}{cc}a& b\\ c& d\end{array}\right]\cdot \left[\begin{array}{cc}e& f\\ g& h\end{array}\right]\\ C& =& A\cdot B\end{array}$$

which takes $8$ multiplies and $4$ additions of $(n/2)\times (n/2)$ sub matrices
$$\begin{array}{rcl}T(n)& =& 8T(n/2)+\Theta (n^2)\\ & =& \Theta (n^3)\end{array}$$

and is no better than the ordinary algorithm. Strassen modified the algorithm so that it can be done in $7$ multiplies and $18$ additions/subtractions
$$\begin{array}{rcl}T(n)& =& 7T(n/2)+\Theta (n^2)\\ & =& \Theta (n^{\log 7})\end{array}$$

where $\log 7\approx 2.81$.

The best to date algorithm is $T(n)\approx \Theta (n^{2.376})$ which is of theoretical interest only.

例

二分图(匈牙利,KM算法详解)
指派问题——匈牙利法

附录

渐进分析（Asymptotic Analysis）

在分析时间复杂度时，我们往往只关心在 $n\to \infty$ 时 $T(n)$ 的增长趋势。引入上界 $O$ （upper bounds）、下界 $\Omega$ （lower bounds）和紧界 $\Theta$ （tight bounds）的数学定义

O ( g ( n ) ) = { f ∣ ∃ c > 0 , lim ⁡ n → ∞ f ( n ) / g ( n ) ≤ c } Ω ( g ( n ) ) = { f ∣ ∃ c > 0 , lim ⁡ n → ∞ f ( n ) / g ( n ) ≥ c } Θ ( g ( n ) ) = O ( g ( n ) ) ∩ Ω ( g ( n ) ) \begin{array}{rcl} O(g(n)) &=& \{f \vert \exist c>0,\lim_{n\rightarrow\infty} f(n)/g(n) \le c\}\\ \Omega(g(n)) &=& \{f \vert \exist c>0,\lim_{n\rightarrow\infty} f(n)/g(n) \ge c\}\\ \Theta(g(n)) &=& O(g(n)) \cap \Omega(g(n)) \end{array} O(g(n))Ω(g(n))Θ(g(n))​===​{f∣∃c>0,limn→∞​f(n)/g(n)≤c}{f∣∃c>0,limn→∞​f(n)/g(n)≥c}O(g(n))∩Ω(g(n))​

类似可以定义严格上界和严格下界

$$\begin{array}{rcl}o(g(n))& =& O(g(n))\setminus \Theta (g(n))\\ \omega (g(n))& =& \Omega (g(n))\setminus \Theta (g(n))\end{array}$$

为了方便，公式中使用集合来表示其中的任何一个元素

A set in a formula represents an anonymous function in the set

举例来说， $n^2+O(n)=O(n^2)$ 表示

$$\forall f\in O(n),\exists h\in O(n^2),\text{ s.t. }{n}^2+f(n)=h(n)$$

运算律

O ( c f ( n ) ) = O ( f ( n ) ) O ( f ( n ) ) + O ( g ( n ) ) = O ( max ⁡ { f ( n ) , g ( n ) } ) O ( f ( n ) ) + O ( g ( n ) ) = O ( f ( n ) + g ( n ) ) O ( f ( n ) ) ⋅ O ( g ( n ) ) = O ( f ( n ) ⋅ g ( n ) ) \begin{array}{rcl} O(cf(n)) &=& O(f(n))\\ O(f(n))+O(g(n)) &=& O(\max\{f(n),g(n)\})\\ O(f(n))+O(g(n)) &=& O(f(n)+g(n))\\ O(f(n))\cdot O(g(n)) &=& O(f(n)\cdot g(n)) \end{array} O(cf(n))O(f(n))+O(g(n))O(f(n))+O(g(n))O(f(n))⋅O(g(n))​====​O(f(n))O(max{f(n),g(n)})O(f(n)+g(n))O(f(n)⋅g(n))​

定理

$$\begin{array}{rcl}\log (n!)& =& \Theta (n\log n)\\ {\sum }_{i=1}^{n}1/i& =& \Theta (\log n)\end{array}$$

参考

写一手漂亮的伪代码