【二分图】785. 判断二分图

题目描述

存在一个 无向图 ，图中有 n 个节点。其中每个节点都有一个介于 0 到 n - 1 之间的唯一编号。给你一个二维数组 graph ，其中 graph[u] 是一个节点数组，由节点 u 的邻接节点组成。形式上，对于 graph[u] 中的每个 v ，都存在一条位于节点 u 和节点 v 之间的无向边。该无向图同时具有以下属性：

• 不存在自环（graph[u] 不包含 u）。
• 不存在平行边（graph[u] 不包含重复值）。
• 如果 v 在 graph[u] 内，那么 u 也应该在 graph[v] 内（该图是无向图）
• 这个图可能不是连通图，也就是说两个节点 u 和 v 之间可能不存在一条连通彼此的路径。

二分图 定义：如果能将一个图的节点集合分割成两个独立的子集 A 和 B ，并使图中的每一条边的两个节点一个来自 A 集合，一个来自 B 集合，就将这个图称为 二分图 。

如果图是二分图，返回 true ；否则，返回 false 。

示例：

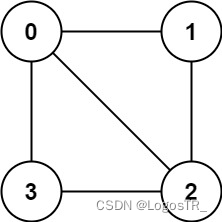
输入：graph = [[1,2,3],[0,2],[0,1,3],[0,2]]
输出：false
解释：不能将节点分割成两个独立的子集，以使每条边都连通一个子集中的一个节点与另一个子集中的一个节点。

解题思路

摆在脸上的二分图题，可以参考这篇。
思路概述：

1. 根据dislikes[]构建邻接链表graph；
2. 分为红蓝两组；
3. 初始化color[]数组表示各结点尚为染色：下标为结点编号，数组值为颜色0 -- 为染色、1 -- 红色、2 -- 蓝色；
4. 随机结点开始染为红色，之后遍历所有未染色的结点，之所以要遍历是因为graph可能不是连通图！
5. 根据邻接链表graph对邻居结点染色：对尚未染色的结点染当前结点相反的颜色、对已染色的结点校验本此着色是否于当前颜色冲突；
6. 存在冲突立即返回false;
7. 完成所有结点染色则返回true。

代码实现

class Solution {
public:
    bool isBipartite(vector<vector<int>>& graph) {
        int n = graph.size();
        vector<int> color(n);
        for(int i = 0; i < n; i++){
            if(color[i] == 0 && !dfs(graph, color, i, 1)) return false;
        }
        return true;
    }

    bool dfs(vector<vector<int>>& graph, vector<int>& color, int node, int colour){
        if(color[node] != 0) return color[node] == colour;
        color[node] = colour;
        int neibourColor = colour == 1 ? 2 : 1;
        for(int& i : graph[node]){
            if(!dfs(graph, color, i, neibourColor)) return false;
        }
        return true;
    }
};

运行结果：