目标:搭建一个能够【识别猫】的简单的神经网络
数据集介绍
- train_set_x_orig :保存的是训练集里面的图像数据(本训练集有209张64x64的图像)。
- train_set_y_orig :保存的是训练集的图像对应的分类值(【0 | 1】,0表示不是猫,1表示是猫)。
- test_set_x_orig:保存的是测试集里面的图像数据(本训练集有50张64x64的图像)。
- test_set_y_orig :保存的是测试集的图像对应的分类值(【0 | 1】,0表示不是猫,1表示是猫)。
- classes :保存的是以bytes类型保存的两个字符串数据,数据为:[b’non-cat’ b’cat’]。
图像是209张 大小为64*64的三通道图片,把图像【拉平】,【标准化】之后,即可用于训练
数据拉平后
训练集降维最后的维度: (12288, 209)
训练集_标签的维数 : (1, 209)
测试集降维之后的维度: (12288, 50)
测试集_标签的维数 : (1, 50)
模型搭建
这里搭建的是简单的Logistic回归,即只有1层的神经网络(输入层不算),且仅有一个结点

对于一张图片(一个样本的训练)
参数初始化
初始化 w w w和 b b b
- w太大,会导致梯度消失;w随机数乘以0.001之后就正常了
为什么w可以设置为0矩阵?
- 如果w = 0矩阵,同一层的多个神经元的计算结果相同,增加结点就没有意义了。但是在本例中,只有一个神经元,因而初始化为0与初始化随机数结论一样
前向传播
线性变换之后得到的值z:
w
w
w是形状为(12288,1)的矩阵
z
(
i
)
=
w
T
x
(
i
)
+
b
z^{(i)} = w^Tx^{(i)} + b
z(i)=wTx(i)+b
激活值:
y
^
(
i
)
=
a
(
i
)
=
s
i
g
m
o
i
d
(
z
(
i
)
)
\hat y^{(i)} = a^{(i)} = sigmoid(z^{(i)})
y^(i)=a(i)=sigmoid(z(i))
损失函数:
L
(
a
(
i
)
,
y
(
i
)
)
=
−
y
(
i
)
log
(
a
(
i
)
)
−
(
1
−
y
(
i
)
)
log
(
1
−
a
(
i
)
)
L(a^{(i)},y^{(i)}) = -y^{(i)}\log(a^{(i)}) - (1-y^{(i)})\log(1-a^{(i)})
L(a(i),y(i))=−y(i)log(a(i))−(1−y(i))log(1−a(i))
成本函数:
J
=
1
m
∑
i
=
1
n
L
(
a
(
i
)
,
y
(
i
)
)
J = {1 \over m} \displaystyle\sum_{i=1}^n L(a^{(i)},y^{(i)})
J=m1i=1∑nL(a(i),y(i))
反向传播
d
(
c
o
s
t
)
d
a
=
−
y
a
+
(
1
−
y
)
(
1
−
a
)
{d(cost) \over da} = -{y\over a} + {(1-y) \over (1-a)}
dad(cost)=−ay+(1−a)(1−y)
d
a
d
z
=
a
(
1
−
a
)
{da \over dz} = a(1-a)
dzda=a(1−a)
所以,
d
z
:
:
=
d
(
c
o
s
t
)
d
z
=
a
−
y
dz ::={d(cost) \over dz} = a - y
dz::=dzd(cost)=a−y
d
w
:
:
=
d
(
c
o
s
t
)
d
w
=
x
∗
d
z
T
dw ::={d(cost) \over dw} = x * dz^T
dw::=dwd(cost)=x∗dzT
d
b
:
:
=
d
(
c
o
s
t
)
d
b
=
d
z
db ::= {d(cost) \over db} = dz
db::=dbd(cost)=dz
梯度下降更新参数
α
\alpha
α为学习率
w
:
=
w
−
α
d
w
w := w - \alpha dw
w:=w−αdw
b
:
=
b
−
α
d
b
b := b - \alpha db
b:=b−αdb
前向传播,反向传播,迭代n次,记录每一步的【成本函数】cost
前向传播-预测predict
经过
s
i
g
m
o
i
d
sigmoid
sigmoid函数之后,输出的概率在[0,1)之间。
将概率转换成【独热编码】one-hot encoding。
如果概率>0.5输出1,否则输出0
建议
在python中,将代码写在一个main函数下,然后在if __name__ == '__main__': 下调用,而不是直接写成【语句】的形式,如:
def main():
pass
# 主函数入口
if __name__ == '__main__':
main()
这样写的好处是,避免了python的变量作用域问题。 python变量没有类型,写得好难受
其他
- 函数返回值 可以用assert来检查返回值是否正常,返回一个元组 or 字典
1.1 assert(如果为假,就报错) - 可以用reshape提醒数组的维度
2.1 reshape([])表示这是一个数 - squeeze可以压缩没有用到的维度,如
3.1 [[1,4]] = > [1,4]
3.2 [1] => 1 - plt.plot(二维数组,对应的标签),多次plt.plot()之后,用plt.show()显示
结果
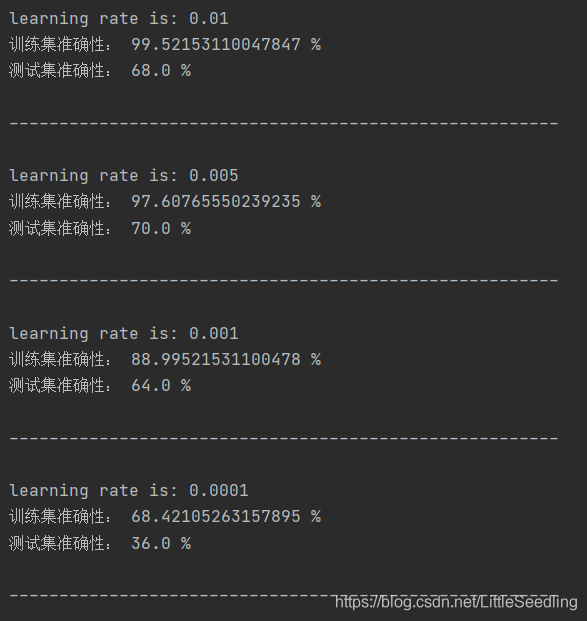
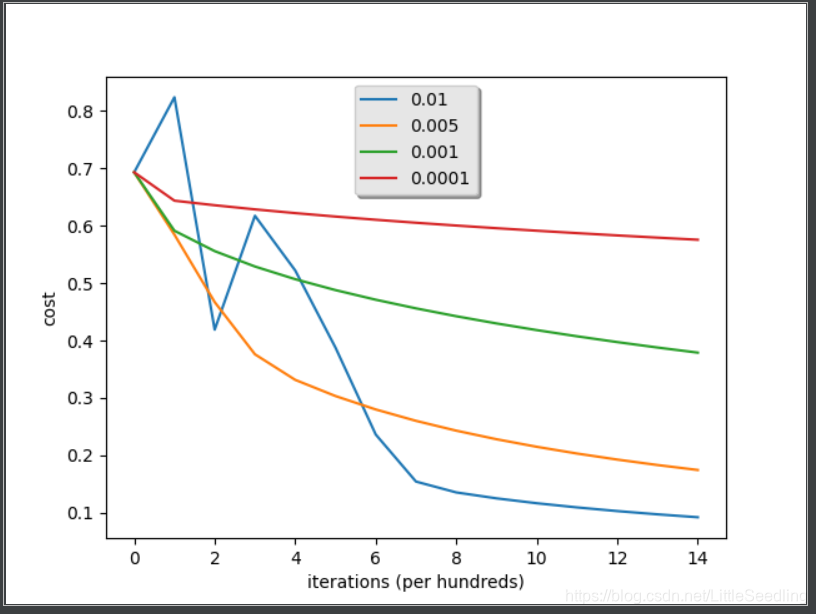






















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








