KD-Tree k近点 HDU 4347

The Closest M Points

Time Limit: 16000/8000 MS (Java/Others)    Memory Limit: 98304/98304 K (Java/Others)
Total Submission(s): 5585    Accepted Submission(s): 1777

Problem Description

The course of Software Design and Development Practice is objectionable. ZLC is facing a serious problem .There are many points in K-dimensional space .Given a point. ZLC need to find out the closest m points. Euclidean distance is used as the distance metric between two points. The Euclidean distance between points p and q is the length of the line segment connecting them.In Cartesian coordinates, if p = (p₁, p₂,..., p_n) and q = (q₁, q₂,..., q_n) are two points in Euclidean n-space, then the distance from p to q, or from q to p is given by:

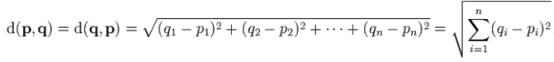
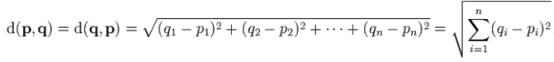
Can you help him solve this problem?

 

Input

In the first line of the text file .there are two non-negative integers n and K. They denote respectively: the number of points, 1 <= n <= 50000, and the number of Dimensions,1 <= K <= 5. In each of the following n lines there is written k integers, representing the coordinates of a point. This followed by a line with one positive integer t, representing the number of queries,1 <= t <=10000.each query contains two lines. The k integers in the first line represent the given point. In the second line, there is one integer m, the number of closest points you should find,1 <= m <=10. The absolute value of all the coordinates will not be more than 10000.
There are multiple test cases. Process to end of file.

 

Output

For each query, output m+1 lines:
The first line saying :”the closest m points are:” where m is the number of the points.
The following m lines representing m points ,in accordance with the order from near to far
It is guaranteed that the answer can only be formed in one ways. The distances from the given point to all the nearest m+1 points are different. That means input like this:
2 2
1 1
3 3
1
2 2
1
will not exist.

 

Sample Input

3 2
1 1
1 3
3 4
2
2 3
2
2 3
1

 

Sample Output

the closest 2 points are:
1 3
3 4
the closest 1 points are:
1 3

 

题意：在一个 k 维的空间上有 n 个点，给出一个点的坐标，输出离这个点最近的 m 个点

第一行有两个数 n k ，接下来 n 行输入 n 个点的坐标，接下来 一个整数 t 表示有 t次询问

每次询问 先输入一个点的坐标，然后输入一个 m 值，找出 离这个点最近的m个点，然后输出

思路：KD-Tree 的经典模板题

KD-Tree：

建树：假设现在是一个3维空间，这颗树的建立是通过点坐标的位置顺序来确定的

当前是3维的话，第一个先出来x轴，从所有点中找到x坐标处于中间位置（n个点中 x坐标为第 n/2 大的）的点a，把它放在根节点的位置，然后这个点的左儿子是y坐标在 a 点下面的所有点中 y轴处于中间位置的点 b，右儿子则是 y坐标在 a 点下面的所有点中 y 坐标处于 中间位置的点 c，然后 b 和 c 的儿子则是根据z坐标来分，然后又是x，y，z，按照这个顺序把所有点分完

查询：输入了一个点的坐标之后，从根节点开始，进行深搜，往接近目标点的方向搜，一边搜的时候，每一个点都记录一个与目标点的距离，递归到底的时候开始回溯，一边往栈里面放，使用优先队列。当存满 m 个点的时候，就开始拿当前点与队头点（当前维度下，已经取了的最边边的点）进行对比，如果当前点更小则换掉，否则就从这个点另一边去深搜，最后所有点被搜完后队列里就是最近的m个点了

#include<iostream>
#include<cstring>
#include<algorithm>
#include<cstdio>
#include<cmath>
#include<queue>
using namespace std;
#define Pow(x) (x) * (x)
#define maxn 50005
#define lson rt << 1
#define rson rt << 1 | 1
#define Pair pair<double,node>

int n,k,idx;

struct node{
	int feature[5];		// 维度 
	bool operator < (const node &u) const{
		return feature[idx] < u.feature[idx];	//根据第 idx 维坐标从小到大排序 
	}
} _data[maxn];

priority_queue<Pair>Q;

struct KDTree{
	node data[4 * maxn];
	int flag[4 * maxn];
	void Build(int l,int r,int rt,int dept){
		if(l > r)
			return ;
		flag[rt] = 1;
		flag[lson] = flag[rson] = -1;
		idx = dept % k;
		idx = dept % k;
		int mid = (l + r) >> 1;
		nth_element(_data + l,_data + mid,_data + r + 1); //找到第 mid 小的数，其实就是中间值 
		data[rt] = _data[mid];
		Build(l,mid - 1,lson,dept + 1);
		Build(mid + 1,r,rson,dept + 1);
	}
	void Query(node p,int m,int rt,int dept){
		if(flag[rt] == -1)
			return ;
		Pair cur(0,data[rt]);
		printf("now is %d %d\n",cur.second.feature[0],cur.second.feature[1]);
		for(int i = 0;i < k;i++)
			cur.first += Pow(cur.second.feature[i] - p.feature[i]);
		int dim = dept % k;
		bool fg = 0; // 标记是否需要继续搜 
		int x = lson;
		int y = rson;
		if(p.feature[dim] >= data[rt].feature[dim]) //往接近的方向搜 
			swap(x,y);
		if(~flag[x])
			Query(p,m,x,dept + 1);
		if(Q.size() < m){ // 递归出来后，如果点数不够，那么这个点就是当前最近的了，进队 
			Q.push(cur); 
			printf("cha ru %d %d\n",cur.second.feature[0],cur.second.feature[1]);
			fg = 1;	//后面有可以被更新
		}else{
			if(cur.first < Q.top().first){ // 对比当前和队顶的，取距离小的那个 
				Pair ppp = Q.top();
				printf("pop %d %d\n",ppp.second.feature[0],ppp.second.feature[1]);
				Q.pop();
				Q.push(cur);
				printf("cha ru %d %d\n",cur.second.feature[0],cur.second.feature[1]);
			}
			if(Pow(p.feature[dim] - data[rt].feature[dim]) < Q.top().first){
				fg = 1;	
			}
		}
		if(~flag[y] && fg)
			Query(p,m,y,dept + 1);
	}
}kd;

void Print(node data){
	for(int i = 0;i < k;i++)
		printf("%d%c",data.feature[i],i == k - 1 ? '\n' : ' ');
}

int main(){
	while(scanf("%d %d",&n,&k) != EOF){
		for(int i = 0;i < n;i++)
			for(int j = 0;j < k;j++)
				scanf("%d",&_data[i].feature[j]);
		kd.Build(0,n - 1,1,0);
		int t,m;
		scanf("%d",&t);
		while(t--){
			node p;
			for(int i = 0;i < k;i++)
				scanf("%d",&p.feature[i]);
			scanf("%d",&m);
			while(!Q.empty())
				Q.pop();
			kd.Query(p,m,1,0);
			printf("the closest %d points are:\n", m);
			node tmp[25];
			for(int i = 0;!Q.empty();i++){
				tmp[i] = Q.top().second;
				Q.pop();
			}
			for(int i = m - 1;i >= 0;i--)
				Print(tmp[i]);
		} 
	}
	return 0;
}