K-nearest neighbors
K-nearest neighbors is a non-parametric machine learning model in which the model memorizes the training observation for classifying the unseen test data. It can also be called instance-based learning. This model is often termed as lazy learning, as it does not learn anything during the training phase like regression, random forest, and so on. Instead, it starts working only during the testing/evaluation phase to compare the given test observations with the nearest training observations, which will take significant time in comparing each test data point. Hence, this technique is not efficient on big data; also, performance does deteriorate when the number of variables is high due to the curse of dimensionality.
KNN voter example
KNN is explained better with the following short example. The objective is to predict the party for which voter will vote based on their neighborhood, precisely geolocation (latitude and longitude). Here we assume that we can identify the potential voter to which political party they would be voting based on majority voters did vote for that particular party in that vicinity so that they have a high probability to vote for the majority party. However, tuning the k-value (number to consider, among which majority should be counted) is the million-dollar question (as same as any machine learning algorithm):

In the preceding diagram, we can see that the voter of the study will vote for Party 2. As within the vicinity, one neighbor has voted for Party 1 and the other voter voted for Party 3. But three voters voted for Party 2. In fact, by this way, KNN solves any given classification problem. Regression problems are solved by taking mean of its neighbors within the given circle or vicinity or k-value.
# -*- coding: utf-8 -*-
"""
Created on Sat Oct 20 15:56:32 2018
@author: LlQ
"""
import numpy as np
import operator as op
def createDataSet():
#each object has a data point with two attributes(one row) and a label
dataPointsArr = np.array([
[1.0,1.1],
[1.0,1.0],
[0,0],
[0,0.1]
])
categoriesList = ['A','A','B','B']
return dataPointsArr, categoriesList
def getManhattanDistance(dataPointList, dataSetMat, q=1):
#or numOfObj=len(categories)
numOfPoints = dataSetMat.shape[0]#number of objects or dataPoints
#shape[0]:one dimention array shows number of elements
# :two dimentions array shows how many rows-dataPoints
# columns:features/attributes
#convert a dataPoint to a matrix which has same shape with dataSetMat
##rowReps columnReps
dataPointMatrix = np.tile(dataPointList, (numOfPoints, 1))####array
#[0,0],
#[0,0],
#[0,0],
#...
#[0,0] #array((numOfPoints, 2))
#|x1-x2|^q + |y1-y2|^q + ... #q=2
#sum(axis=1): do sum for each row
distanceP = (np.power(np.abs(dataPointMatrix - dataSetMat),q)).sum(axis=1)
distanceArr = np.power(distanceP, 1.0/q) #q=2
return distanceArr #vector #one dimension array
def getEuclideanDistance(dataPoint, dataSetMat):#between dataPoint and datapoints in dataSetMat
#|x1-x2|^q + |y1-y2|^q + ... #q=2
distanceArr=getManhattanDistance(dataPoint, dataSetMat, q=2)
return distanceArr
def classify0(dataPoint, dataSetMat, categoriesList, k):
#get a distance list
distanceArr = getEuclideanDistance(dataPoint, dataSetMat)
#get an ordered index array(indices) based on comparision of the distances
sortedDistIndexArr = np.argsort(distanceArr)
# np.argsort() we do not sort the values but the indices based on values in distanceArr
#[0]:3-lowest in distanceArr [1]:2 [2]:0 [3]:1-longest in distanceArr
#one dimension
#np.arsort(): horizontal ########
#two dimension array
#np.arsort(x,axis=0): vertical
#np.arsort(x,axis=1): horizontal
classCount={}
#top k
for i in range(k):#k<=4 since we just have 4 objects/pts and usually k<=20
#k<= len(sortedDistIndexArr)
category = categoriesList[sortedDistIndexArr[i]]
classCount[category]=classCount.get(category,0)+1
#such as classCount has a key 'A' with value 1, then plus 1
#such as classCount append a key 'B' with value 0, then plus 1
#op.itemgetter(1) = by value
sortedClassCount=sorted(classCount.items(), key=op.itemgetter(1),
reverse=True)
return sortedClassCount[0][0] #tupleList: [ (‘B’, 2) ,(‘A’,1) ]
def file2matrix(filename):
openFile = open(filename)
rDataByLines = openFile.readlines()
#create an numberOfLines * 3 matrix
numberOfLines = len(rDataByLines)
dataMatrix=np.zeros((numberOfLines, 3))
classLabelsList= []
index=0
labelDict={}
#save data to returnMatrix
for line in rDataByLines:
line = line.strip() # to remove front and end space
columnDataList=line.split('\t')
#append
dataMatrix[index,:] = columnDataList[0:3]# save data by row/line
index+=1
#create a dict-labels with last item in columnDataList
if columnDataList[-1] not in labelDict:
#labels[columnDataList[-1]]=len(labelDict)+1 # {?:1,:2,?:3}
labelDict[columnDataList[-1]]=3-len(labelDict)
classLabelsList.append(labelDict[columnDataList[-1]])
return dataMatrix, classLabelsList, labelDict
def autoNorm(dataSet):
minVals = dataSet.min(0)#The 0 in the dataSet.min(0) allow you to take the
maxVals = dataSet.max(0)#minimums from the columns, not the rows.
ranges = maxVals - minVals
#newValue = (originalValue-min)/(max-min)
normDataSet = np.zeros(np.shape(dataSet)) #create a new matrix
m = dataSet.shape[0] #how many rows
normDataSet = dataSet - np.tile(minVals, (m,1))
normDataSet = normDataSet/np.tile(ranges, (m,1))
return normDataSet, ranges, minVals
def datingClassTest():
holdRatio = 0.10#holdRatio: 10% of data to test the classifier, 90% to train
#read data from the file and
datingDataMat, realClassList, labelDict = file2matrix('datingTestSet.txt')
#normalization
normalDataMat, ranges, minVals = autoNorm(datingDataMat)
rows=normalDataMat.shape[0]
rowsTestDataMat = int(rows*holdRatio)
errorCount=0.0
#using test_dataset to test the classifier
for i in range(rowsTestDataMat):
#def classify0(dataPoint, dataSet, class, k):
predictedClass = classify0(normalDataMat[i,:], \
normalDataMat[rowsTestDataMat:rows,:],
realClassList[rowsTestDataMat:rows],\
3)#90% of data to train |^^^\
#realClassList is the right or true class we known
print("the classifier came back with: %d, the real answer is: %d" \
% (predictedClass, realClassList[i]))
if(predictedClass != realClassList[i]):
errorCount += 1.0
print("The total error rate is %f" % (errorCount/float(rowsTestDataMat)) )
def classifyPerson():
resultList = ['not at all', 'in small doess', 'in large doses']
percentGameTime = float(input(\
"Percentage of time spent playing video game?"))
flyMiles = float(input("frequent flier miles earned per year?"))
iceCreamLiters=float(input("liters of ice cream consumed per year?"))
datingDataMat, factClassList, labelDict = file2matrix('datingTestSet.txt')
normDatingDataMat, ranges, minValArr = autoNorm(datingDataMat)
dataPointsArr = np.array([flyMiles, percentGameTime, iceCreamLiters])
predictedClass=classify0((dataPointsArr-minValArr)/ranges,\
normDatingDataMat,factClassList,3)
print('predictedClass: ', predictedClass)
print("You will probably like this person: ",\
resultList[predictedClass-1])
#a handwriting recognition system
#store all characters of a file in the NumPy array(one row)
def img2vector(filename):
#create a array with 1*1024
return1DimArr = np.zeros((1,1024))
fr=open(filename)
#32*32 data in the file
for i in range(32): #total 32 rows
lineStr = fr.readline() #get each line data(string form)
for j in range(32): #total 32 digits(32 columns of char)
return1DimArr[0, 32*i+j] = int(lineStr[j])
return return1DimArr
#Test: KNN on handwritten digits
from os import listdir
def handwrittingClassTest():
trainingDigitClassList = []
#Get contents of trainingDigits directory
trainingFileList = listdir('trainingDigits')
numOfFiles = len(trainingFileList)
trainingDataMat = np.zeros((numOfFiles,1024))
for i in range(numOfFiles):
#Process class-number from filename
fileNameStr = trainingFileList[i] # 0_0.txt
fileName = fileNameStr.split('.')[0] # 0_0
digitClass = int(fileName.split('_')[0]) # 0
trainingDigitClassList.append(digitClass)
#get processed training data-matrix
trainingDataMat[i,:]=img2vector('trainingDigits/%s' % fileNameStr)
#Get contents of testDigits directory
testFileList = listdir('testDigits')
errorCount = 0.0
numOfTestFiles = len(testFileList)
for i in range(numOfTestFiles):
testFileNameStr = testFileList[i] # 0_0.txt
testFileName = testFileNameStr.split('.')[0] # 0_0
#testDigitClass[i] is real digit class
testDigitClass = int(testFileName.split('_')[0]) # 0
#get processed test data-matrix
testData1DimArr = img2vector('testDigits/%s' % testFileNameStr)
predictedDigitClass = classify0(testData1DimArr, \
trainingDataMat, \
trainingDigitClassList, 3)
print("The classifier came back with %d, the real answer is: %d" \
% (predictedDigitClass, testDigitClass))
if(predictedDigitClass != testDigitClass):
errorCount += 1.0
print("\n The total number of errors is: %d" % errorCount)
print("\nThe total error rate is: %f" % (errorCount/float(numOfTestFiles)))
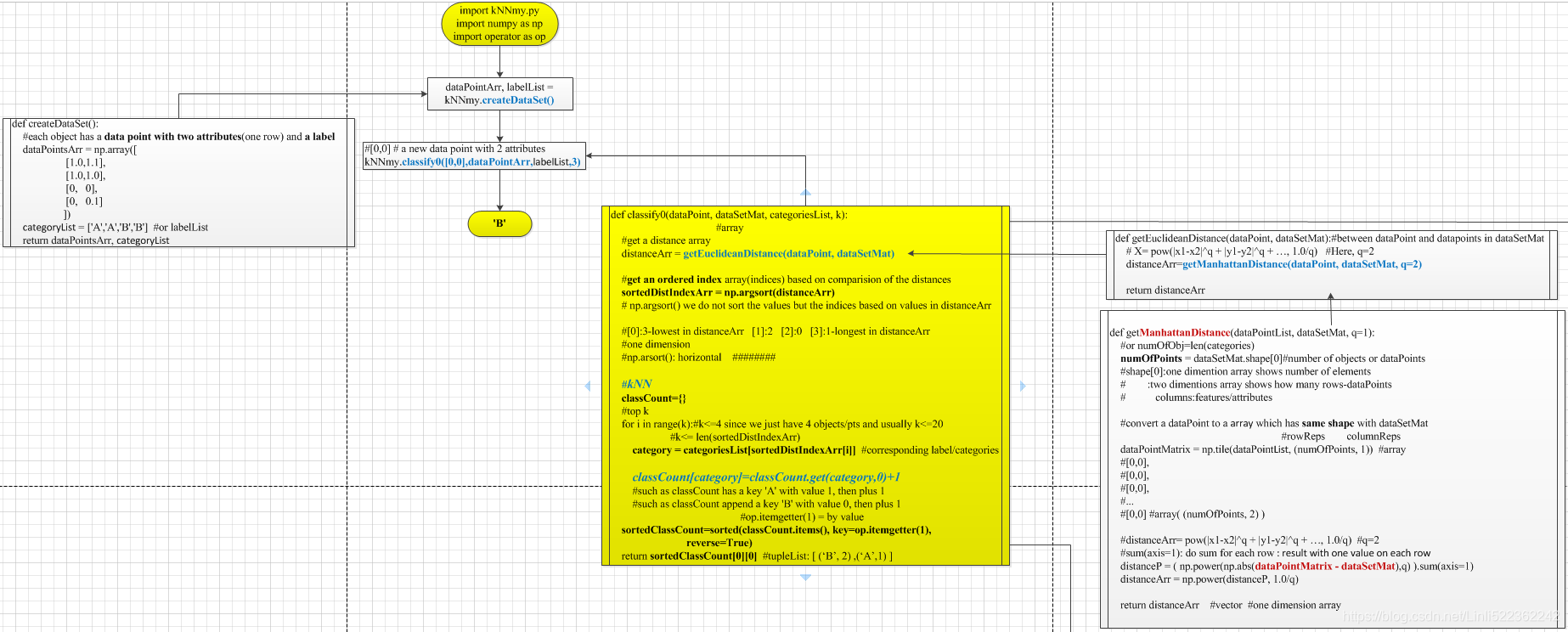



 K近邻算法原理与应用示例
K近邻算法原理与应用示例





 本文介绍了K近邻(KNN)算法,它是一种非参数机器学习模型,在测试阶段才开始工作,不适合大数据和高维数据。文中通过选民投票示例解释了KNN的分类原理,还给出了Python代码实现,包括创建数据集、计算距离、分类等,并进行了约会数据和手写数字识别的测试。
本文介绍了K近邻(KNN)算法,它是一种非参数机器学习模型,在测试阶段才开始工作,不适合大数据和高维数据。文中通过选民投票示例解释了KNN的分类原理,还给出了Python代码实现,包括创建数据集、计算距离、分类等,并进行了约会数据和手写数字识别的测试。
















 3577
3577

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








