全双工MIMO系统联合优化

全双工MIMO系统中的联合收发器优化与自干扰抑制

拉德瓦·苏丹§，IEEE会员，卡里姆·G·塞迪克∗，IEEE高级会员，韩竹† ∗∗，IEEE会士，以及贝赫纳姆·阿藏‡， IEEE会士
电气与计算机工程系，曼哈顿学院，里弗代尔，纽约州，美国 电子与通信工程系，开罗美国大学，新开罗，埃及 †电气与计算机工程系，休斯顿大学，得克萨斯州，美国 ∗∗计算机科学与工程系，庆熙大学，首尔，韩国
‡电气与计算机工程系，莱斯大学，休斯顿，美国rsultan02@manhattan.edu, kseddik@aucegypt.edu,zhan2@uh.edu,aaz@rice.edu

摘要

本文研究了发射和接收天线联合选择对全双工（FD）多输入多输出（MIMO）网络性能的影响。天线选择问题通常是一个组合问题，其复杂度随天线数量呈指数增长。为了全面理解天线选择的影响，我们研究了具有全双工MIMO基站（BS）的单小区网络中的和速率最大化问题。首先，我们考虑具有常规规模MIMO全双工基站的系统，即常规规模全双工MIMO系统。针对两种不同场景研究了和速率最大化问题；在第一种场景中，我们联合优化发射和接收天线选择、预编码器以及接收机权重。提出了一种基于广义Benders分解的算法来求解混合整数非线性的和速率最大化问题。在第二种场景中，我们考虑通过零迫（ZF）传输实现自干扰消除。提出了一种启发式算法，通过优化发射天线、接收天线以及自干扰被置零的接收天线的选择来求解和速率最大化问题。其次，在超大规模即大规模MIMO系统中，我们分别推导了采用零迫接收机和预编码器时上行链路和下行链路速率的下界。通过联合优化发射天线与接收天线比例以及自干扰被置零的接收天线比例来最大化和速率。最后，通过数值分析评估了所提出的和速率最大化问题的性能。

关键词. 天线选择，渐近行为，全双工，广义Bender分解，大规模MIMO，资源分配，发射波束成形

一、引言

全双工（FD）通信和大规模多输入多输出（MIMO）被认为是能够满足现代蜂窝网络中不断增长的通信链路容量需求的重要候选技术。理论上，启用全双工通信可使半双工（HD）通信所达到的数据速率提高一倍。通常，自干扰（SI）——即全双工节点自身发射对其接收产生的干扰——被视为实现全双工的主要障碍，直到自干扰消除技术的发展[1]–[3]。此外，大规模MIMO[4]–[6]已证明其能够提高频谱效率与常规规模MIMO系统相比，通过大幅增加天线数量有助于扩展网络容量，从而提升了通信可靠性和网络性能。此外，当使用海量天线时，最简单的用户检测和/或波束成形方法（例如匹配滤波器（MF）或零迫（ZF））即可达到最优性能。

然而，在MIMO通信网络中使用全双工（FD）带来了一些新的挑战[7]–[9]。第一个挑战是如何优化发射与接收天线选择。对于工作在半双工（HD）模式下的给定MIMO基站（BS），所有天线将分别在下行链路（DL）或上行链路（UL）模式下全部用于发射或接收。然而，对于工作在全双工（FD）模式下的MIMO‐BS，我们需要选择发射天线和接收天线的数量及其编号。这一决策高度依赖于基站天线与网络用户之间的信道条件，且该选择会显著影响系统性能。因此，为了优化网络性能，必须优化发射和接收天线的选择。

此外，为了使全双工MIMO可行，需要降低自干扰（SI）。然而，随着天线数量的增加，模拟自干扰消除电路的复杂度也随之增长。因此，为防止接收器的射频（RF）饱和，需要通过发射波束成形来实现自干扰消除。结果，第二个挑战是设计满足两个目标的全双工下行链路（FD‐DL）预编码器：第一个目标与下行链路半双工（DL‐HD）预编码器类似，即减少多用户干扰（MUI）的影响；第二个目标是降低自干扰（SI）水平。

A. 贡献

在本文中，基于上述挑战，我们研究了不同的天线选择场景以及发射器‐接收器联合优化方案，以最大化全双工MIMO基站和多个用户的单小区网络中的可达和速率。我们的贡献总结如下：

1) 在常规规模全双工MIMO系统中，我们提出了一种通过联合优化发射天线选择、接收天线选择、发射预编码器权重和接收机权重的和速率最大化问题。因此由于天线选择的组合特性，所提出的优化问题是混合整数非线性规划（MINLP）问题，我们使用广义Benders分解（GBD）算法来求解该问题。

2) 在常规规模全双工MIMO系统中，为了研究考虑自干扰消除的影响，我们假设基站采用零迫发射预编码器和零迫接收机。在此情况下，零迫预编码器有助于降低上行链路接收时的自干扰功率。因此，我们提出一个通过联合优化发射天线选择、接收天线选择以及自干扰消除的和速率最大化问题。为了更好地优化自干扰消除，我们需要在零迫预编码器用于消除自干扰的基站接收天线上，最优地选择接收天线数量。通过零迫发射波束成形实现自干扰消除的主要思想是设计下行链路预编码器，使其在基站接收天线处抑制自干扰。然而，增加所需的干扰抑制数量会减少下行链路传输中的自由度，从而降低下行链路传输增益，这在选择用于自干扰消除的接收天线数量时引入了权衡。在此场景下，为了避免求解组合式天线选择问题带来的复杂度增长，我们提出了一种启发式的低复杂度天线选择算法。

3) 在大规模全双工MIMO系统中，类似于常规规模的全双工MIMO设置，我们考虑通过零迫使能进行自干扰消除。在这种情况下，零迫预编码器有助于降低影响上行链路接收的自干扰功率。为了理解网络的渐近行为，我们推导了上行链路和下行链路速率的下界。基于这些下界，我们研究了下行速率与增加用于零迫预编码器消除自干扰的接收天线数量之间的权衡关系。然而，在发射天线和接收天线数量趋于无穷大的假设下，所有天线在渐近意义上是等效的。因此，无需优化发射和接收天线的具体索引，只需优化其相对于总天线数量的比例即可。最后，我们提出了一个速率区域最大化问题，以优化发射天线与接收天线比例以及零迫预编码器用于消除自干扰的接收天线所占比例。

本文的其余部分组织如下。在第二节中，概述了在全双工MIMO网络资源分配方面的一些前期工作。在第三节中，阐述了系统模型。在第四节中，提出了全双工大规模MIMO网络中的和速率最大化问题。在第五节中，在大规模MIMO场景下研究了渐近速率行为，并提出了速率区域最大化问题。数值结果在第六节中给出。最后，第七节对全文进行了总结。

符号说明： 向量用粗体小写字母表示，矩阵用粗体大写字母表示。随机实体 z的统计期望由 E(z)表示。复数域用 C 表示。主要数学符号列于表1中。

符号	符号	符号	定义
N	N	N	基站天线数量
Nt	Nt	Nt	发射天线数量
Nr	Nr	Nr	接收天线数量
Na K	Na K	Na K	接收天线数量在以下情况下 自干扰通过发射波束成形被消除 宏用户数量
Kd	Kd	Kd	下行链路宏用户数量
Ku	Ku	Ku	上行链路宏用户数量
Pd	Pd	Pd	下行链路传输功率
Pu	Pu	Pu	上行链路传输功率
Hd	Hd	Hd	下行链路信道矩阵
hk,i	hk,i	hk,i	kth下行链路和 ith上行链路用户之间的信道
Ha	Ha	Ha	之间的信道比例 基站发射和接收天线之间的信道 自干扰将被消除的位置
Hr Hsi	Hr Hsi	Hr Hsi	基站发射和接收天线之间信道的比例 基站发射与接收天线之间的信道 自干扰不会被消除的位置 自干扰信道矩阵
Ht	Ht	Ht	聚合下行信道矩阵
Wd	Wd	Wd	下行预编码矩阵
FZF	FZF	FZF	下行零迫预编码矩阵
WZF	WZF	WZF	归一化下行零迫预编码矩阵
wk Uu	wk Uu	wk Uu	kth下行用户预编码向量 上行接收矩阵
xk G	xk G	xk G	kth下行用户发送信号 上行信道矩阵
Uu	Uu	Uu	上行接收矩阵
UZF	UZF	UZF	零强迫上行接收矩阵
ul CBS	ul CBS	ul CBS	lth上行用户的接收向量 自干扰消除系数
yd,k	yd,k	yd,k	kth下行用户接收信号
yu,l	yu,l	yu,l	lth上行链路用户接收信号
Γdl	Γdl	Γdl	kth宏下行链路用户接收信干噪比
Γul	Γul	Γul	l th宏上行链路用户接收信干噪比
ΓZF dl	ΓZF dl	ΓZF dl	k th采用零迫的宏下行链路用户接收信干噪比
ΓZF ul Rd	ΓZF ul Rd	ΓZF ul Rd	l th采用零迫的宏上行链路用户接收信干噪比 下行速率下界
Ru	Ru	Ru	上行速率下界
Rs	Rs	Rs	单位时间与带宽的总速率
RZF	RZF	RZF	使用ZF时单位时间与带宽的总速率
a t\n	a t\n	a t\n	n th antenna transmission coefficient
a sic\n	a sic\n	a sic\n	n th antenna SI cancellation coefficient
σ	σ	σ	2加性高斯白噪声方差
α	α	α	接收天线比例 在其上消除自干扰
β	β	β	发射与接收天线之间的比率

二、先前工作

随着自干扰消除技术的发展，针对不同全双工系统的资源分配方案的开发已引起近期一些研究工作的关注[10],[11]。此外，作者在[12]中表明，全双工在无干扰感知和有干扰感知场景下均能优于半双工。因此，为了在考虑部署全双工带来新挑战的同时充分利用可用的全双工资源，迫切需要高效且新颖的资源分配方案[13]–[15]。此外，研究大规模MIMO网络的潜力以及增加有源天线数量可能带来的好处，是近期研究工作的主要关注点[16]–[19]。

如第一节所述，在MIMO网络中使用全双工通信会带来在基站处选择最佳发射天线和接收天线组合的问题。在[20],中，提出了一种联合和速率最大化问题，旨在优化基站在时相和用户分配下的半阵列天线模式选择。此外，作者还考虑了一种通用的最大‐最小速率优化方法，以在满足上行链路和下行链路速率给定比例的前提下，最大化每个用户的最小速率。在[21],中，作者推导了采用发射天线选择（TAS）的全双工空间复用（SM）‐MIMO系统的中断概率和符号错误概率的精确闭式表达式。此外，通过数值分析，作者评估了有无TAS情况下全双工SM‐MIMO系统的性能。在[22],中，提出了一种基于天线选择的干扰消除方法用于全双工MIMO系统，其中通过天线选择和特征波束成形实现干扰消除。在[23],中，作者研究了全双工放大转发中继中最大‐最大天线选择的中断概率，其中源、中继和目的均配备多根天线。在[24],中，研究了双节点全双工MIMO网络的天线选择问题。假设每个节点都配备了预定义数量的天线和发射/接收链。所提出的天线选择算法基于幅值、正交性和行列式准则。在[25],中，作者研究了双向全双工MIMO系统中的多种天线选择方案。在研究最优天线选择方案后，作者提出了一种复杂度较低的近最优方案，该方案采用贪婪搜索方法。结果表明，所提算法相比随机天线选择具有15%的性能增益。在[26],中，提出了两种基于最大和速率和最小符号错误率的天线选择方案。通过数值分析表明，这些方案能够实现显著的性能增益。然而，这些选择增益依赖于自干扰的抑制程度。

此外，全双工MIMO中的自干扰消除最近吸引了更多研究工作。在[27],中提出了一种基于波束的自适应滤波器结构，并采用模拟最小均方（ALMS）环路，以降低全双工MIMO系统中自干扰消除的复杂度。此外，结果表明，所提出的结构优于应用于全双工单输入单输出系统的ALMS环路。在[28],中，作者提出了一种采用特征波束成形（EB）结合零点导向的自干扰抑制方法。该自干扰抑制方法依赖于通过对MIMO天线进行精心布置来调控传播信道，使中继站处的自干扰信道矩阵秩退化，使得特征模式数量接近于一。在[29],中，作者提出了一种天线选择算法以减少服从莱斯分布的自干扰。所提出的准则通过最大化期望信号功率与残余自干扰及噪声之比，从而最小化残余自干扰的影响。在[30],中提出了用于两级自干扰消除方案的两种估计算法。第一阶段在射频自干扰消除中，推导出一种基于压缩感知的自干扰信道估计算法；第二阶段为了联合估计残余自干扰信道、目标信道以及发射机非线性，提出了一种基于子空间的算法；结果表明该所提出的算法比最小二乘算法具有更好的性能。

此外，在[31]中研究了全双工大规模MIMO网络中的自干扰消除。研究了一种在存在相位噪声的单射频链路全双工大规模MIMO正交频分复用（OFDM）系统中的数字自干扰消除方法。推导出一种加权线性自干扰信道估计器，以最小化每个OFDM符号中的残余自干扰功率。在[32],中，作者研究了两种部分模拟自干扰消除方法：第一种方法中，模拟消除器被分配给一组固定的天线；另一方面，在第二种方法中，模拟消除器可根据信道条件动态分配至任意接收天线。在[33],中，假设自干扰信道的瞬时信道状态信息（CSI）不可用，作者提出了一种基于能效优化的自干扰消除（SIC）方案（EE‐SIC）。该技术可有效消除自干扰并提高系统能量效率。在[34],中表明，在全双工大规模MIMO网络中，当信道状态信息完美时，自干扰减除在自干扰消除方面优于空间抑制；然而，在非完美信道估计情况下，空间抑制将实现更高的上行链路和总遍历速率。在[35],中，作者为全双工多天线基站和具有两个有源天线的半双工移动终端提出了一种机会式用户与天线选择算法。该算法根据上行链路用户的向量信道增益选择其天线，根据下行链路用户的信号干扰噪声比（SINR）选择其天线。在[36],中，作者研究了一个具有莱斯自干扰信道的全双工大规模MIMO网络，同时采用带有自干扰消除功能的线性零迫预编码器，并在上行链路全双工移动终端上使用感知自干扰的分数功率控制机制。结果表明，利用大规模MIMO有助于克服上行链路速率瓶颈。

III. 系统模型

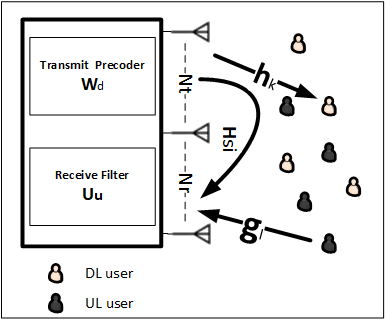
我们考虑一个具有单个 N根天线的全双工MIMO基站的无线网络。在全双工传输假设下，该基站配备了一个全双工无线电以帮助抑制自干扰。此外，基站天线被划分为 Nt根发射天线和 Nr根接收天线。网络中有 K个半双工单天线用户，这些用户被分为 Kd个在下行链路模式下接收的用户和 Ku个在上行链路模式下发送的用户。本文研究了两种不同的场景。在第一种场景中，我们假设采用通用预编码器和通用接收器，并将在后续对其进行优化以最大化和速率。在第二种场景中，我们研究在基站部署零迫预编码器和零迫接收机后网络的变化。接下来，我们将从接收到的上行链路信号、接收到的下行链路信号以及接收机的SINR三个方面区分这两种场景。

A. 全双工MIMO网络

在这种情况下，我们假设基站具有下行链路预编码器，其预编码矩阵为W d ∈ CNt × K d，以及具有接收矩阵Uu ∈ CKu × N r的上行链路接收器。此外，还应保证 Nt ≥ Kd和Nr ≥ Ku 1。系统模型如图1a所示。基于上述假设，下行链路用户接收到的信号由 kth给出

$$
yd,k=\sqrt{Pd}h_k w_k x_k \quad \text{Desired Signal} + \sum_{j=1, j \neq k}^{Kd} \sqrt{Pd}h_k w_j x_j \quad \text{MUI} + \sum_{i=1}^{Ku} \sqrt{Pu}h_{k,i}s_i \quad \text{CCI} + n^d_k,
$$

其中 Pd为下行链路传输功率，hk ∈ C1×Nt是基站发射天线与半双工下行用户之间的下行链路信道向量。不失一般性，假设所有信道系数均为独立同分布（i.i.d.）的零均值复高斯随机变量，且具有单位方差，即我们采用瑞利平坦衰落信道模型[39]–[41]。此外，假设信道状态信息（CSI）在基站和用户端均完全已知。向量wk ∈ CNt ×1是预编码矩阵W d ∈ CNt ×Kd的第 kth列，表示用于第 kth个下行链路用户数据的预编码向量， xk是第 kth个下行链路用户的发送信号，其中E{‖xk‖ 2 }= 1。第二项是网络中其他下行链路传输引起的多用户干扰（MUI）。第三项是来自上行链路用户的上行链路传输所引起的同频干扰（CCI），其中 P u为上行链路传输功率。本文假设所有 K u个上行链路用户的发射功率恒定在所提出的模型中，假设 K d 和 K u 分别表示在同一时频资源块上服务的活跃下行链路和上行链路用户的数量。换句话说，网络可能拥有更多的下行链路和上行链路用户，但用户选择不在本文的研究范围内。因此，这些条件对下行链路传输中的预编码和上行链路传输中的接收器滤波器都是必需的[ 37 ] , [ 38 ]。 2在理想信道状态信息下的结果可作为全双工系统和速率性能的上限。

功率 Pu[42]–[44]。hk,i 是上行链路用户与下行链路用户之间的信道系数，ith kth si 是具有 ith 的上行链路用户发送信号， E{‖si‖ 2}= 1是具有方差 nd k 的下行链路加性白复高斯噪声（AWGN）项。根据公式(1)的表达式，下行链路接收SINR在 σ2下行链路用户处为

$$
\Gamma_{dl} = \frac{P_d |h_k w_k|^2}{\sigma^2 + \sum_{j=1, j \neq k}^{Kd} P_d |h_k w_j|^2 + \sum_{i=1}^{Ku} P_u |h_{k,i}|^2}.
$$

另一方面，在上行链路传输的情况下，基站从 lth上行链路用户传输 l ∈{1, 2, · · ·, Ku}接收到的信号由以下公式给出

$$
yu,l=\sqrt{Pu}u_l g_l s_l \quad \text{Desired Signal} + \sum_{i=1, i \neq l}^{Ku} \sqrt{Pu}u_l g_i s_i \quad \text{MUI} + \sqrt{CBS}\sqrt{Pd}u_l H_{si} W_d x_d \quad \text{RSI} + u_l n_u,
$$

其中，ul ∈ C1×Nr是 l th上行链路传输数据的接收向量，g l ∈ CNr ×1是 l th上行链路发射机与基站接收天线之间的上行链路信道向量。(3)式中的第二项是网络中其他上行链路传输对 l th上行链路用户造成的多用户干扰；第三项是残余自干扰信号。该残余自干扰信号由全双工无线电在基站引入的自干扰消除系数0 ≤ C B S ≤ 1的平方根、下行链路传输功率、上行链路接收向量 u l 、基站发射和接收天线之间的自干扰信道矩阵H si ∈ CNr × N t、下行预编码矩阵W d 以及发送的下行链路信号x d ∈ C K d × 1 [45]相乘得到。最后，n u ∈ C N r × 1是方差为 σ 2的加性高斯白噪声向量。因此，基站接收天线处 l th上行链路用户的接收信干噪比为

$$
\Gamma_{ul} = \frac{P_u |u_l g_l|^2}{\sigma^2 |u_l|^2 + \sum_{i=1, i \neq l}^{Ku} P_u |u_l g_i|^2 + CBS P_d |u_l H_{si} W_d x_d|^2}.
$$

由(2)和(4)中的表达式可得，单位时间单位带宽的总速率为

$$
Rs = \sum_{k=1}^{Kd} C_1 \log_2(1+ \Gamma_{dl}) + \sum_{l=1}^{Ku} C_2 \log_2(1+ \Gamma_{ul}),
$$

其中 C1和 C2是常数缩放因子。

B. 带零迫预编码器和零迫接收机的全双工MIMO网络

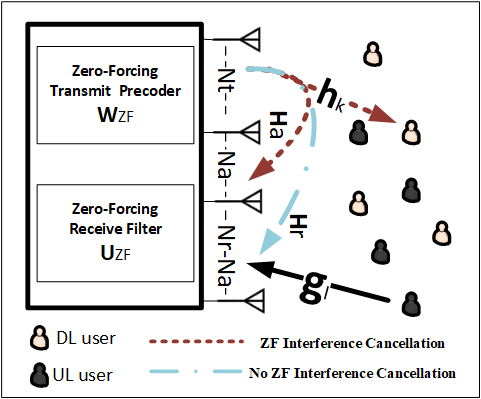
通常，在HD‐MIMO网络中，零迫预编码器和接收器分别用于消除下行链路传输与上行链路传输之间的多用户干扰。然而，在FD‐MIMO网络中，除了消除下行链路的多用户干扰外，下行链路发射预编码器还将旨在对部分基站接收天线上的自干扰进行置零。通过将这部分基站接收天线视为一组额外的虚拟下行链路用户，并在这些天线上消除干扰，从而降低自干扰水平。由于在预编码器设计中考虑自干扰消除会降低下行链路传输增益，因此我们提出一个变量 0 ≤ Na ≤ min(Nr, Nt − Kd)，表示零迫预编码器通过发射波束成形来消除自干扰的基站接收天线数量。当 Na= 0时，发射波束成形不会在任何基站接收天线上消除自干扰，即零迫预编码器仅消除下行链路传输之间的多用户干扰。另一方面，当 Na= Nr时，预编码器将在所有基站接收天线上消除自干扰。最后，当 1< Na< Nr − 1时，预编码器仅在Na个接收天线上消除自干扰。相应地，应保证Nt ≥(Kd+ Na)，以具备足够的维度来传输下行链路数据，并在目标下行链路用户和基站接收天线上消除干扰。系统模型如图1b所示。

基于上述假设， kth下行链路用户接收到的信号由以下公式给出

$$
yd,k|ZF=\sqrt{Pd}h_k w^ZF_k x_k \quad \text{Desired Signal} + \sum_{i=1}^{Ku} \sqrt{Pu}h_{k,i}s_i \quad \text{CCI} + n^d_k,
$$

其中wZF k ∈ C(Nt ) ×1是第 kth个下行链路用户数据的零迫预编码向量。第二项是由 Ku个上行链路用户的上行链路传输引起的共道干扰。零迫预编码矩阵F ZF ∈ C(Nt )×(Na +K d) 和归一化预编码矩阵WZF ∈ C (Nt )×(Na +K d) 分别由以下给出，

$$
F^{ZF} = H_t^H(H_t H_t^H)^{-1},
W^{ZF} = \frac{F^{ZF}}{|F^{ZF}|_F},
$$

其中，Ht =[Hd H a] T ∈ C( N a +K d )×( N t )是聚合下行信道矩阵，由下行链路信道矩阵Hd =[h1 h 2 · · · hKd ] T ∈ CKd ×N t和基站发射与接收天线之间的信道Ha ∈ CNa ×N t构成，该信道在自干扰被消除的位置。 ‖FZF ‖ F 表示弗罗贝尼乌斯范数预编码矩阵FZF。比较(1)和(6)中的表达式可以明显看出，使用ZF发射预编码器能够消除多用户干扰项。根据(6)的表达式，下行链路接收SINR在 kth下行链路用户处可表示为

$$
\Gamma^ZF_{dl} = \frac{P_d |h_k w^ZF_k|^2}{\sigma^2 + \sum_{i=1}^{Ku} P_u |h_{k,i}|^2}.
$$

另一方面，在上行链路传输情况下，基站接收到的来自 lth上行链路传输 l ∈{1, 2, · · ·, Ku}的信号由以下公式给出

$$
yu,l|ZF=\sqrt{Pu}u^ZF_l g_l s_l \quad \text{Desired Signal} + \sqrt{CBS}\sqrt{Pd}u^ZF_l H^{ZF}_{si} W^{ZF} x^{ZF} \quad \text{RSI} + u^ZF_l n_u,
$$

其中uZF l ∈ C1×Nr是上行链路传输数据的ZF接收向量。ZF上行链路接收矩阵UZF ∈ CKu×Nr由下式给出

$$
U^{ZF}=(GHG)^{-1}GH,
$$

其中G ∈ CNr×Ku=[g1 g2 ··· gKu]是上行链路发射机与基站接收天线之间的上行信道矩阵3 r] T ∈ C Nr×Nt 9 ZF si=[ a 。式（）中的第二项为残余自干扰功率，HHH是基站发射与接收天线之间的信道。在采用零迫预编码器的情况下，HZF si由Ha和Hr ∈ C Nr−Na×(Nt)组成，其中后者是基站发射天线与接收天线之间的信道，该部分的自干扰仅通过全双工无线电自干扰消除进行抑制，而无法通过发射预编码器消除。此外，xZF=[x d 0Na] T ∈ C(Kd +N a )×1是聚合的下行链路发射信号，由下行链路用户信号xd ∈ C K d× 1以及发送至基站接收天线用于自干扰消除的零信号 0Na ∈ C N a× 1构成。类似地，比较表达式（3）和（9）可以发现，在接收端使用零迫技术可消除多用户干扰项。因此，上行链路用户在基站接收天线处的接收信干噪比为

$$
\Gamma^ZF_{ul} = \frac{P_u |u^ZF_l g_l|^2}{\sigma^2 |u^ZF_l|^2 + CBS P_d |u^ZF_l H^{ZF}_{si} W^{ZF} x^{ZF}|^2},
$$

根据(8)和(11)中的表达式，单位时间单位带宽的和速率为

$$
RZF = \sum_{k=1}^{Kd} C_1 \log_2(1+ \Gamma^ZF_{dl}) + \sum_{l=1}^{Ku} C_2 \log_2(1+ \Gamma^ZF_{ul}).
$$

其中 C1和 C2是常数缩放因子。

IV. 全双工MIMO网络中的和速率最大化

在本节中，我们研究第三节所提模型的和速率最大化问题。对于第三节‐A中的模型，优化将针对 N t、 N r、预编码向量以及接收向量进行。对于第三节‐B中的模型，由于采用零迫预编码器和接收器，因此优化将针对 N t 、 N r 和 N a 进行。应当

(7)中的下行链路预编码矩阵的归一化是为了限制基站发射的功率。然而，在上行链路传输中，(10)中的上行接收矩阵的归一化并非必需。

需要注意的是，对 Nt、 Nr和 Na的优化取决于基站已知的信道状态信息（CSI）量，因此在优化 Nt、 Nr和 Na的值时，还应考虑天线选择问题。换句话说，我们不仅要选择每个子集中天线的数量，还应选择发射和接收天线的具体索引。为此，我们定义二进制变量 at|n ∈{0, 1}、 n ∈{1, 2, · · · N}。当 at|n= 1时，第 nth根天线被用作发射天线；否则，第 nth根天线被用作接收天线。相应地，Nt=∑ N n=1 at|n和Nr= N −∑N n=1 at|n=∑ N n=1（1 − at|n）。此外，在零迫（ZF）情况下，我们定义二进制变量asic|n ∈{0, 1}、n ∈{1, 2, · · · N}。当 asic|n= 1时，零迫预编码器在第 nth根天线上将自干扰（SI）置零；否则，零迫预编码器不在第 nth根天线上消除自干扰。如果第 nth根天线被配置为发射天线，即at|n= 1，则asic|n将自动设为零。接下来，我们将分别针对第三节‐A和第三节‐B中提出的两个模型，建立并求解和速率最大化问题。

A. 全双工MIMO网络中的联合收发器优化

在这种情况下，我们通过优化 Nt、 Nr、预编码器权重和接收器权重来最大化和速率。此外，我们还确定发射和接收天线的索引 4。相应地，和速率最大化问题可表述为

$$
\max_{at,Wd,Uu} Rs
$$

subject to

$$
\sum_{n=1}^{N} at|n \geq Kd,
\sum_{n=1}^{N} (1 - at|n) \geq Ku,
Pd \sum_{k=1}^{Kd} |w_k|^2 \leq P_{max},
at|n \in {0, 1}, \forall n \in {1, \cdots, N},
$$

(P1)

其中at是一个包含所有 at|n变量的向量。第一个约束条件保证发射天线数量大于下行链路用户数量。第二个约束条件保证接收天线数量大于上行链路用户数量。第三个约束条件是将总的下行链路传输功率限制在 Pmax以内， Pmax为允许的最大发射功率 5。该表达形式在(P1)未对上行链路和下行链路传输施加最小速率约束。这一假设已被许多研究工作采用[8],[49],[50]。然而，在没有最小速率约束的情况下最大化和速率可能会导致用户之间的公平性问题。文献[48] 中的作者通过最大化对数效用函数来解决该问题，从而在系统吞吐量和公平性之间取得良好的平衡。(P1)中的优化问题是一个混合整数非线性规划问题，由于存在at|n的二进制变量，该问题很难求解。此外，应注意的是， Nt和 Nr 的值及其索引分别控制着Wd 和Uu 矩阵的维度，即Wd ∈ CNt×Kd 和Uu ∈ CKu×Nr。因此，无法将 (P1)中的问题分解为两个独立的子问题来分别处理整数变量和连续变量。为了求解(P1)中的问题，我们首先将其重新表述为关于Wex ∈ C N×Kd（扩展预编码矩阵）、U ex ∈ CKu×N（扩展接收矩阵）以及At|ex（一个对角矩阵，其对角线元素为at）的形式。在这种情况下，改变 Nt 和 Nr 的值不会影响Wex 和Uex的维度。接下来，我们基于 Wex、Uex和At|ex 定义和速率

$$
Rex = \sum_{k=1}^{Kd} \log_2 \left(1+ \frac{P_d |h_k|ex A_t|ex w_k|ex|^2}{\sigma^2 + \sum_{j=1, j \neq k}^{Kd} P_d |h_k|ex A_t|ex w_j|ex|^2 + \sum_{i=1}^{Ku} P_u |h_{k,i}|^2} \right) + \sum_{l=1}^{Ku} \log_2 \left(1+ \frac{P_u |u_l|ex (I_N - A_t|ex) g_l|ex|^2}{\sigma^2 |u_l|ex (I_N - A_t|ex)|^2 + \sum_{i=1, i \neq l}^{Ku} P_u |u_l|ex (I_N - A_t|ex) g_i|ex|^2 + CBS P_d |u_l|ex (I_N - A_t|ex) H_{si}|ex A_t|ex W_{ex} x_{ex}|^2} \right),
$$

其中

$$
CCI_{ex} = \sum_{i=1, i \neq l}^{Ku} P_u |u_l|ex (I_N - A
ex) g_i|ex|^2,
$$

$$
RSI_{ex} = CBS P_d |u_l|ex (I_N - A_t|ex) H_{si}|ex A_t|ex W_{ex} x_{ex}|^2,
$$

hk|ex ∈ C1×N是第 kth个下行链路用户与所有基站天线之间的扩展下行链路信道，wk|ex ∈ CN×1是扩展预编码矩阵Wex的第 kth 列，ul|ex ∈ C1×N是扩展发射机矩阵Uex的第 lth行，g l|ex ∈ C N×1是第 lth个上行链路用户与所有基站天线之间的扩展上行链路信道，而Hsi|ex ∈ C N×N是基站天线之间的信道矩阵。因此，(P1*)中的和速率最大化问题可以重新表述为

$$
\max_{A_t | ex ,W_ex ,U_ex} Rex
$$

subject to

$$
\text{Tr}(A_t|ex) \geq Kd,
N - \text{Tr}(A_t|ex) \geq Ku,
P_d |W_{k|ex}|^2 \leq P_{max},
A_t|ex(n, n) \in {0, 1} \quad \forall n \in {1, \cdots, N},
$$

(P1*)

其中第一个约束确保 N t =Tr(At|ex)（即At|ex的对角元素之和）超过 K d ，第二个约束保证 N r = N−N t = N−Tr(At | ex)超过 K u 。

为了求解问题(P1*)，该问题是一个混合整数非线性规划问题，我们采用GBD算法。接下来，我们将给出GBD算法的概述，以及如何利用它来求解（P1*）中的问题。

1) FD-MIMO网络中联合收发器优化的GBD算法：

GBD是一种用于求解包含连续变量和整数变量的混合整数非线性规划问题的求解方法[51]。GBD的主要思想是将混合整数非线性规划问题分解为两个子问题：原始问题和主问题。原始问题与连续变量相关，通过将At|ex变量的值固定在某个可行点At|ex处，并以Wex和Uex的形式重写问题而得到。第二个子问题称为主问题，仅与整数变量相关。这两个问题被迭代地求解，直到它们的解收敛。在每次迭代中，根据原始问题的可行性，向主问题添加最优性割或可行性割。

为了使用GBD求解（P1*）中的混合整数非线性规划问题，第一步是在设定At|ex=At|ex后构造原始问题，如下所示 6

$$
\min_{Wex,Uex} - Rex|At|ex
$$

subject to

$$
P_d |W_{ex}|^2 \leq P_{max}.
$$

(P1.1*)

如果原始问题可行，则更新解的上界（UBD），然后需要计算该可行迭代的最优性割，该最优性割将在后续用于构建主问题。每个可行迭代 j1= 1, · · · J1的最优性割由下式给出

$$
L(A_t|ex, \mu_{j1}) = \min_{W_{ex},U_{ex}} (-Rex + \mu^T G(A_t|ex, W_{ex}, U_{ex})).
$$

(16)

然而，如果原始问题不可行，则需要计算该不可行迭代的可行性割，该可行性割将类似地用于主问题的构建。对于每个不可行迭代的 j2= 1, · · · J2，其可行性割由下式给出

$$
L_2(A_t|ex , \lambda_{(j2)}) = \min_{W_{ex},U_{ex}} (\lambda^T G(A_t|ex , W_{ex}, U_{ex})),
$$

(17)

其中，可行性割是通过求解可行性问题得到的。该可行性问题由以下给出

$$
\max_{\lambda} \min_{W_{ex},U_{ex}} \lambda^T G(A_t|ex , W_{ex}, U_{ex}),
$$

(Q)

6GBD要求初始值At | ex应为满足(P1*)中前两个约束的优化问题集中的任意可行点。

其中 G(At|ex,Wex,Uex))表示在(P1)中定义的约束函数。下一步是将主问题表述如下，

$$
\min_{A_t|ex,\gamma} \gamma
$$

subject to

$$
\gamma \geq L(A_t|ex, \mu_{j1}), \quad j1= 1, \cdots, J1,
0 \geq L_2(A_t|ex, \lambda_{j2}), \quad j2= 1, \cdots, J2.
$$

(P1.2*)

求解主问题后，我们更新解的下界（LBD）。如前所述，原始问题和主问题被迭代地求解，直到它们的解（即上界 UBD和下界LBD）收敛。

为求解（P1.1**）中的原始问题，我们采用文献 [52],[53]中提出的内凸近似（NOVA）算法。NOVA算法的思想是求解一系列强凸的内逼近问题（P1.1**）。接下来，我们将简要概述NOVA算法，并讨论如何利用它来求解（ P1.1**）中的原始问题。

2) 非凸优化约束下的NOVA算法概述：假设一个非凸目标函数 Q的最小化问题 K→ R，其定义在凸集 K上，并受到一些凸约束和一些非凸约束zj(x) ≤ 0的限制，其中 zj： K→ R，

$$
\min_x Q(x) \quad \text{subject to} \quad z_j(x) \leq 0, \quad j= 1, \cdots, m, \quad x \in K,
$$

(P)

其中(P)的可行域表示为 X。NOVA算法的主要目标是高效地计算(P)的局部最优解，同时保持迭代过程7的可行性。给定 xν ∈ X，该方法求解一系列形式为(P)的强凸内逼近问题序列。

$$
\min_x \tilde{Q}(x; x_\nu) \quad \text{subject to} \quad \tilde{z} j(x, x \nu) \leq 0, \quad j= 1, \cdots, m, \quad x \in K,
$$

(Px ν)

˜其中， Q(x;xν)和 z˜j( x, xν)分别表示在当前迭代点xν处对 Q(x)和 zj( x)的近似，且 X(xν)˜为(Px ν)的可行域。Q(x;xν)是定义在 K上的强凸函数，且对于所有y ∈ X，z˜ j( ·, y)在 K上是凸的。可以证明每个子问题(Px ν)都是强凸的，因此具有唯一解，记为ˆx(xν)：

$$
\hat{x}(x_\nu) = \arg\min_{x \in X(x_\nu)} \tilde{Q}(x; x_\nu).
$$

(18)

随后，利用算法1获得(Px ν)的解。从一个初始可行点x 0,出发，所提出的方法迭代地计算问题(18)的解ˆx(x ν )，然后从x ν向ˆx(x ν )方向进行一步更新。在步骤S.1中，需要检查当前解的平稳性。S.1步骤中合适的终止条件是 ‖ˆx(x ν )−x ν‖ ≤ ε n，其中ε n 为期望的精度。此外，我们采用递减步长规则来更新γ ν：

对于感兴趣的读者，NOVA算法的收敛条件在[ 52 ]中给出。

数据：所有信道状态信息， ε0

1)初始化上界 UBD 和下界 LBD

2)如果 UBD ≤ LBD+ ε0 那么

(A∗ t|ex,瓦∗ ex,U ∗ ex)是该问题的解； 求el解se原始问题

如果原始问题（P1.1**）是可行的，那么

求解原始问题并获得解和乘数（W∗ ex，U ∗ e x µ ∗); 确定 L(At|ex, µK1)；

如果 −Rex(At|ex, W∗ ex, U ∗ ex)< UBD，则设置UBD= −Rex(At|ex,瓦∗ ex,U∗ ex);

else求解Q中的可行性问题并获得其解(瓦∗ ex,U ∗ ex, λ ∗); 确定 L2(At|ex, λ(J2))；

end end

3)求解（P1.2*）中的主问题并获得其解(γ∗, A∗ t|ex)

4)设置 LBD= γ∗；

5)设置At|ex=A∗ t|ex； 6)返回步骤2； 算法2:全双工MIMO网络中的联合收发器优化

$$
\gamma_\nu = \gamma_{\nu-1}(1 - \varepsilon\gamma_{\nu-1}), \quad \nu \geq 1,
$$

(19)

其中 γ0 ∈(0, 1]且 ε ∈(0,1)。有关NOVA算法以及 γ、 ε和 ε选择的更多细节，请参见[52],[53]。在所提出的原始问题 (P1.1**)中，我们仅需˜为目标函数 Rex推导出一个近似 Rex。如[52],所建议， Rex的一个有效选择是 Rex的一阶近似，即

$$
\tilde{Rex} = \sum_{i=1}^{I} \tilde{Rex}(x_i,x_\nu),
$$

其中每一项

$$
\tilde{Rex}(x_i, x_\nu) = \nabla_{x_i} Rex(x_\nu)^T (x_i - x_{\nu i}) + \frac{\tau_i}{2} |x_i - x_{\nu i}|^2
$$

(20)

其中xi 是i th 变量块。在问题中，

$$
{ T K d +K u } { 1 \cdots K d T K d +1 \cdots 1 | ex \cdots K d | ex T 1 | ex \cdots T K u | ex }
x,x,x,xw,,w,u,,u。
$$

相应地，our = the 原始问题的近似由以下给出，

$$
\min_{W_{ex},U_{ex}} - \tilde{Rex}|A_t | ex
$$

subject to

$$
P_d |W_{ex}|^2 \leq P_{max}.
$$

(P1.1**)

随后，我们可以采用算法1来求解（P1.1**）中的原始问题近似。针对（P1*）的完整求解算法在算法2中给出。在初始化 UBD和LBD后，我们使用NOVA算法（即算法1）求解原始问题。然后，根据原始问题的可行性，向主问题添加最优性割或可行性割。下一步是求解主问题并更新LBD。该算法将在原始问题与主问题之间持续迭代，直到它们的解收敛，如算法2中的第二步所示。

B. 全双工MIMO网络中联合发射天线、接收天线与自干扰消除的优化：基于零强制预编码器和零强制接收机

在这种情况下，我们试图找到使网络和速率最大化的 Nt、 Nr和Na的最优值。此外，我们还需要确定将自干扰置零的发射天线、接收天线以及接收天线的索引。因此，和速率最大化问题可表示为

$$
\max_{Nt,Nr,Na,aZF_t ,asic} Rs
$$

subject to

$$
Nt \geq Kd+ Na, \quad Nr \geq Ku, \quad 0 \leq Na \leq \min(Nr, Nt − Kd),
\sum_{n=1}^{N} at|n= Nt,
\sum_{n=1}^{N} (1 − at|n)= Nr,
\sum_{n=1}^{N} (1 − at|n)(asic|n)= Na,
$$

(P2)

其中aZF_t是包含所有 at|n系数的向量，asic是包含所有 asic|n系数的向量。(P2)的最优解可通过穷举暴力搜索获得 among

$$
\sum_{Nt=Kd}^{N-Ku} \binom{N}{Nt} \left[\binom{Nr}{1}+\binom{Nr}{2}+ \cdots+ \binom{Nr}{\min(Nr,Nt −Kd)}\right]
$$

情况。因此，对于数量较多的天线而言，穷举搜索在实现上是不切实际的。为此，我们提出了一种启发式两步天线选择算法；在第一步中，我们确定发射和接收天线的索引。在第二步中，我们确定通过发射预编码器消除自干扰的接收天线的索引。

1) FD-MIMO网络中的发射和接收天线选择：在本节中，我们解释了针对第三节‐B中描述的模型所提出的用于选择发射和接收天线的迭代算法。该算法的步骤如算法3所示。初始时，假设在满足(P2)中所述前两个约束的前提下，随机选择天线作为发射或接收天线。根据基站处的信道状态信息，基站天线按照其对所有上行链路和下行链路用户的上行与下行信道增益之和进行降序排列。第一步是从具有最大上行和下行信道增益之和的天线开始，检查将其固定为发射天线或接收天线哪种方式对和速率更有利。在此步骤中，我们不考虑通过零迫发射波束成形实现的自干扰消除。在确定第一个天线的工作模式后，我们转向具有第二大全局上行和下行信道增益之和的天线。类似地，在已知第一个天线模式的情况下，选择第二个天线的模式以获得更高的和速率增益。随后，该算法依次决定

数据：所有信道状态信息，A0t, ε, RS(A0t)；

结果：查找A∗ t=[at|1, at|2, · · ·, at|N]T;

最初： At= A0 t，迭代 j= 1；

1:排序

(a)计算 $$ \lambda_n = \sum_{k=1}^{Kd} |h_{nk}|^2 + \sum_{l=1}^{Ku} |g_{ln}|^2 \quad \forall n \in {1..N}; $$

(b)构造 Λ，使得 Λ(1)= n(max(λn))， Λ(N) = n(min(λn));

2:顺序发射/接收天线选择

对于每个天线：(at|Λ(i)= 1)if RZF|(at|Λ(i)= 1) ≥ RZF|(at|Λ(i)= 0)else(at|Λ(i)= 0)

3:检查收敛性

(a)如果 RZF(Aj t)-RZF(Aj−1 ) ≤ ε1，则 A∗ t= Aj t; else j返=j+1步骤2；

end

算法3：全双工MIMO网络中的发射与接收天线选择

所有其他剩余天线的工作模式。需要注意的是，在每一步中，该算法都会检查设置天线模式是否会违反天线数量的约束。在为所有天线选择完模式后，算法将从第一个天线开始重新迭代选择过程，直到和速率的变化在某一容差范围内为止。应注意，天线选择过程是在基站（BS）处执行的。此外，算法3的复杂度可以通过累加算法中每个操作的复杂度并选取最坏情况下的项（即最高阶项）来确定，该项决定了算法的限制性行为。因此，算法3的计算复杂度为 O(N2)，即具有多项式复杂度。

2) FD-MIMO网络中用于自干扰消除的天线选择：在本节中，我们解释了所提出的迭代算法，该算法用于选择通过零迫发射波束成形实现自干扰消除的接收天线。最初，假设在任何接收天线上均不进行自干扰消除。采用与第四节 IV‐B1中算法类似的方法，根据在该接收天线单独进行自干扰消除时所获得的和速率增益，对每个接收天线进行排序。然后，算法检查在增益最高的天线上进行自干扰消除是否会提高或降低和速率。如果在此天线上进行自干扰消除可提高和速率，则取值为 a sic|n = 1，否则为 a sic|n = 0。接着，算法继续处理增益次高的天线，并基于对第一个天线的决策结果，判断是否在第二个天线上进行自干扰消除。此过程依次对每个接收天线重复执行。注意，在每一步中，算法需检查天线数量的约束是否被违反。随后，算法重复执行该选择过程，直到和速率的变化在某一容差范围内为止。完整的过程如算法4所示。

假设在任何接收天线上均未进行自干扰消除，该算法计算仅在 nth天线上进行自干扰消除时的和速率R′ sn。随后，天线索引按照所能带来的最高和速率增益，在向量C中按降序排列，即C(1)= n(max(R′ sn))，C(N)= n(min(R′ sn))。下一步是检查在更多接收天线上进行自干扰消除对和速率的影响。为此，我们首先假设在满足天线数量约束的前提下，在 C(1)所指示的第一个天线索引 asic|C(i)= 1上进行自干扰消除。接着，在已对C(1)进行自干扰消除的基础上，算法检查额外在C(2)上进行自干扰消除是否会提升和速率。如果该额外的自干扰消除能够提高和速率，则设 asic|C(2)= 1；否则 asic|C(i)= 0。此过程依次对所有接收天线重复执行。之后，算法迭代直至达到某一收敛容差 ε2。需要注意的是，用于自干扰消除的天线选择过程在基站（BS）处执行。最后，通过采用与算法3相同的计算步骤，可得出算法4的计算复杂度为 O(N2)，即具有多项式复杂度。

V. 基于零强迫的全双工MIMO网络的渐近和速率行为

在本节中，我们研究当N= Nt+ Nr→ ∞时的渐近速率行为。我们假设基站配备零迫预编码器和零迫接收机。在这种情况下，我们可以假设 Na= αNr。研究渐近行为的第一步是评估当天线数量趋于无穷大时，下行链路和上行链路速率所受到的影响。首先，在接下来的命题中，我们从研究下行链路传输的行为开始。

命题1。 全双工下行链路速率总和 Rd的下界由以下给出

$$
R_d = K_d \log_2\left(1+ \frac{N_t −(K_d+ N_a)}{(K_d+ N_a)} \left(\frac{P_d}{\sigma^2+ P_u K_u}\right)\right).
$$

(21)

证明： 由(8)可知，总下行链路速率是来自下行半双工用户和全双工节点的下行链路速率之和。因此，可推导出总下行链路速率的下界如下

$$
R_d = K_d E[\log_2(1+ \Gamma^ZF_{dl})],
(a) \geq K_d \log_2\left{ 1+\left[E\left( \frac{1}{\Gamma^ZF_{dl}}\right)\right]^{-1}\right}
(b) = K_d \log_2 \left{1+ \left[E \left(\frac{\sigma^2 + \sum_{i=1}^{Ku} P_u |h_{k,i}|^2}{P_d / |F^{ZF}| F^2} \right) \right]^{-1}\right}
(c) = K_d \log_2\left{ 1+ \frac{P_d}{N_t −(K_d + N_a)} \cdot \frac{1}{(K_d + N_a)( \sigma^2 + E\left{\sum {i=1}^{Ku} P_u |h_{k,i}|^2\right})}\right}
(d) = K_d \log_2\left{ 1+ \frac{N_t −(K_d + N_a)}{K_d + N_a} \left(\frac{P_d}{\sigma^2 + P_u K_u}\right) \right},
$$

(22)

其中，(a)是对凸函数log2(1+ 1/x) 应用詹森不等式，并假设在大规模MIMO系统中，每个半双工下行用户从 K d 用户中“渐近地”经历相同的接收信干噪比，这是由于信道硬化[54],[55] 。(b)源于零强制阵列增益特性，其中FZF Ht=IKd+Na/‖FZF‖F。因此，hkwi= δki/‖FZF‖F，其中 δki= 1 当 k= i时成立，否则为 δki= 0。此外，(c)是通过代入在[56]中计算得到的‖FZF‖F 的值得到的。最后，(d)是通过已知 $\sum_{i=1}^{Ku} |h_{k,i}|^2 \sim E(Ku, 1)$ 服从形状参数为Ku 、单位速率参数的爱尔朗分布，类似地，$\sum_{i=1, i \neq m}^{Ku} |h_{k,i}|^2 \sim E(Ku − 1, 1)$ 服从形状参数为(Ku − 1)、单位速率参数的爱尔朗分布得到的。

在以下命题中，我们给出了当 N→ ∞时上行链路速率的下界。

命题2。全双工上行链路速率 Ru的下界由以下给出

$$
R_u = K_u \log_2\left(1+ \frac{P_u(N_r − K_u)}{\sigma^2+ CBS P_d(1 − \alpha)}\right).
$$

(23)

(23)中的表达式可根据[56, Proposition 2]中的推导得出。

为了阐明通过发射波束成形在下行链路速率与自干扰消除之间的权衡关系，将分别以 β= N t /N r和 α= N a /N r表示的下行链路速率和上行链路速率的下界（如(21)和(23)所示）写为如下形式

$$
R_d(\beta,\alpha) = K_d \log_2\left( 1+ \left(\frac{P_d}{\sigma^2 + P_u K_u}\right) \left(\frac{\beta}{K_d (\beta+1)} N + \alpha - 1\right)\right)
R_u(\beta,\alpha) = K_u \log_2\left( 1+ \frac{P_u\left(\frac{N}{\beta+1} - K_u\right)}{\sigma^2 + CBS P_d(1 −\alpha)} \right).
$$

(24)

根据(24)中推导出的表达式可以很容易地验证，增加 α 能够实现更好的自干扰消除和更高的上行链路速率；然而，这会导致下行链路速率下降。因此，需要优化 β以及 α，以最大化（扩大）网络的速率区域。

A. 用于速率区域最大化的天线比率与自干扰消除优化

在本节中，我们首先推导一个可行速率区域，该区域通过计算 Rd(β, α) 8,的最大值得到；然后对于 Rd(β, α)= R的每一个可能取值，我们优化 β和 α以最大化 Ru(β, α) 9。通过将下行链路速率设为常数值R， β与 α之间的关系由下式给出

$$
\beta(1 −\Psi \frac{K_d}{N}) = \Psi\left(\frac{K_d}{N}+ \alpha\right),
$$

(25)

其中 Ψ= 1+(σ2+PuKu)(2R/Kd−1)Pd。由于 Ψ> 1，(25)中的关系满足 β>(α+ Kd/N)/(1 − Kd/N)。因此，可行速率区域最大化问题可表示为

$$
\max_{\beta,\alpha} R_u(\beta, \alpha)
$$

subject to

$$
0 \leq \alpha \leq 1, \quad \beta > \frac{\alpha+ K_d/N}{1 − K_d/N},
\beta(1 −\Psi \frac{K_d}{N}) = \Psi\left(\frac{K_d}{N}+ \alpha\right).
$$

(26)

为了求解（26）中速率区域最大化问题的解，我们将在以下命题中首先研究目标函数的凸性。

命题3。在给定Nr ≥ 4链路速率 Ru(β, α)关于 β和 α是凸函数。

命题3的证明在[56,附录B]中给出。

因此，我们可以用 β或 α重新表述速率最大化问题，而不会影响问题的凸性。将(26)中 β用 α表示后代入后，速率最大化问题表示为

$$
\max_{\alpha} R_u(\alpha)
$$

subject to

$$
0 \leq \alpha \leq 1.
$$

(P3)

由于目标函数是凸的，该最大化问题的解位于由(P3)中的约束所定义的可行集的边界上。因此，经过一些简单的数学推导，可以很容易地得出，对于给定的 Rd，使 Ru最大化的 α和 β的值为

$$
\alpha^ = 1, \quad \beta^ = \frac{\Psi(1+ K_d/N)}{1 −\Psi( K_d/N)}.
$$

(27)

另一方面，通过将 R u(β, α)的值设为某个常数，也可以导出速率最大化问题

当上行链路传输不活跃时，达到最大下行链路速率9 速率区域也可以通过计算Ru(β,α)的最大值获得，即当下行链路传输不活跃时。然后，对于每个可能的 R u(β,α)值，我们优化 β和 α以最大化 R d (β,α)。

需要注意的是，上行链路速率随 α单调递增。然而，在(P3)中最大化的速率是在固定下行链路速率下的上行链路速率，该速率是 α的凸函数。这是因为在 α较小时，增加α将增加 β以保持 R d 恒定，从而导致上行链路速率下降；而在α较大时（即更多的自干扰消除），增加 β对上行链路速率的影响较小，因此增加 α将提高上行链路速率。因此，在固定下行链路速率下，上行链路速率是 α的凸函数。

数据：所有信道状态信息,At, ε2, RS(At)

结果：查找A∗sic

初始： asic|n= 0, ∀ n ∈{1, 2, · · ·, Nr}, Iteration j= 1;

1.对于 n= 1： N 执行 r

(a) Set asic|m= 0 ∀m ≠ n ∈{1, 2, · · ·, Nr};

Calculate R′ sn; end

2.构造一个向量C，使得C(1)= n(max(R ′ sn)), C(N)= n(min(R′ sn))

3.对于每个天线，如果 RZF|(asic|C(i)= 1) ≥ RZF|(asic|C(i)= 0)那么 asic|C(i)= 1

4.如果 RZF(Aj sic)-RZF(Aj−1 sic) ≤ ε2那么A∗ sic= Aj sic else j=j+1；返回步骤3； 算法4：用于自干扰消除的天线选择

$$
\beta = \frac{N P_u}{P_u K_u + (2R’/K_u - 1)(\sigma^2 + C P_d (1 - \alpha))} - 1.
$$

(28)

需要注意的是，为了保证 β>(α+(Kd/N))/(1 −(Kd/N))，全双工无线电应满足以下条件

$$
CBS \leq \frac{1}{P_d} \left( \frac{P_u(N - K_u)}{2^{R’/K_u} - 1} - \sigma^2 \right).
$$

(29)

因此，速率最大化问题表示为

$$
\max_{\alpha} R_d(\alpha)
$$

subject to

$$
0 \leq \alpha \leq 1.
$$

(P4)

在这种情况下，(P4)中定义的优化问题不是凸的。因此，我们将推导拉格朗日函数，并应用卡鲁什‐库恩‐塔克(KKT)条件[57],[58] 来求解(P4)的对偶问题。(P4)的对偶问题由以下给出

$$
\max_{\alpha,\lambda_1,\lambda_2} L(\alpha, \lambda_1, \lambda_2) = R_d - \lambda_1(\alpha) + \lambda_2(1 - \alpha)
$$

subject to

$$
0 \leq \alpha \leq 1.
$$

(30)

对偶问题的解由以下命题给出。

命题4. 利用KKT条件求解对偶问题的解由以下给出

$$
\alpha = 0, \quad \lambda_1 = \lambda_2 = 0.
$$

(31)

证明：通过应用KKT条件得到的方程组由以下给出

$$
\frac{\partial L(\alpha, \lambda_1, \lambda_2)}{\partial \alpha} = 0, \quad \lambda_1 \times \alpha = 0, \quad \lambda_2 \times (1 - \alpha) = 0.
$$

(32)

经过一些简单的数学步骤，可以证明满足(32)的对偶问题 (30)的解由α= 0, λ1= λ2= 0给出。

需要注意的是，由于优化问题函数在(P3)中关于 α的凸性，通过求解(P3)获得可行速率区域比求解(P4)更为直接。

六、数值分析

在本节中，我们仿真了一个以基站为中心、用户随机分布在网格内的方形网格网络。对于常规规模全双工MIMO系统，我们评估了第四节‐A中提出的联合优化问题的性能，并将其与第四节‐B中提出的采用零迫接收机和预编码器的联合天线选择与自干扰消除方案进行比较。此外，由于第四节‐A和第四节‐B中提出的问题分别为混合整数非线性规划和整数规划(IP)问题，因此需要通过与最优解进行比较来验证其性能。对于第四节‐A中的问题，最优解通过穷举搜索获得，即枚举所有可能的发射和接收天线选择组合；然后对每种组合优化预编码器和接收机权重；最后选择具有最高和速率的组合。类似地，第四节‐B中的问题的最优解也通过穷举搜索获得。最后，我们将联合天线选择与自干扰消除的性能与零迫接收机和预编码器的性能进行比较。

对于常规规模的全双工MIMO系统，图2展示了和速率随上行链路信噪比（SNR）的变化情况，其中上行链路信噪比定义为 Pu/σ 2 ，并比较了第四节‐A和第四节‐B中所提算法与基于最优穷举搜索的解的性能。首先，在 N= 6、 Kd= 3和 Ku= 2条件下对网络进行了仿真。从图2的结果可以看出，在保持上行链路传输功率恒定的情况下，提高上行链路信噪比（即降低噪声方差 σ2）能够提升网络的总和速率。此外，将第四节‐A中提出的联合和速率最大化方案与最优穷举搜索相比，可以验证所提算法能够实现接近最优的性能。类似地，在考虑通过零迫（ZF）进行自干扰消除时，可以验证第四节‐B中提出的天线选择算法也能达到近似最优的性能。然而，当比较两种算法的可实现和速率时，显然第一种算法具有更好的性能。如前所述，增加所需的干扰置零数量会减少下行链路传输中的自由度，从而降低下行链路传输增益，进而影响和速率。因此，我们可以得出结论：在天线选择的同时优化预编码器和发射机权重，比在零迫预编码器和零迫使迫限制下仅优化天线选择能够获得更优的性能。为进一步验证，网络还在 N= 8、 K d = 3和 K u = 2条件下进行了仿真。同样地，通过降低噪声方差来提高上行链路信噪比可以提升和速率 R s 。此外，结果还验证了所提算法能够在低得多的复杂度下逼近最优解。最后，为了研究通过零迫进行自干扰消除的影响，网络采用最小均方误差（MMSE）波束成形和等增益合并（EB）进行了仿真。

从结果中可以看出，通过零迫（ZF）实现的自干扰消除（SI cancellation）具有显著效果，其性能优于最小均方误差（MMSE）和等增益合并（EB）。此外，我们还可以注意到，ZF与MMSE或EB之间的性能差距随着上行链路信噪比（UL SNR）的增加而增大。这是因为通过减小 σ2来提高上行链路信噪比（UL SNR）会增加上行链路