数据结构——线性表

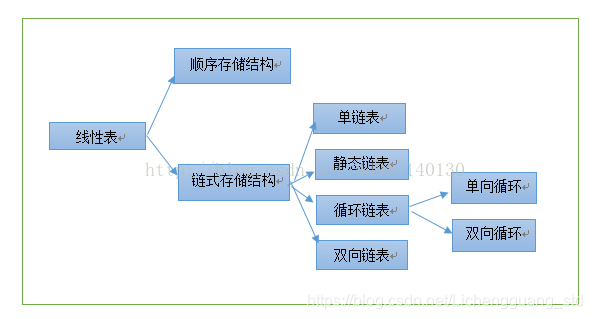
       线性表是数据结构中最为简单的一种数据类型。它是同种数据类型组成的有序序列的线性结构。按照存储结构的不同，线性表可分为两大类：顺序存储结构（顺序表）、链式存储结构（链表）。

                                     

       顺序表实现的方式使用的是数组。所谓顺序表，则是预先在内存空间上申请一块连续的存储地址。基于数组，可实现顺序表的查找、增删等相应的操作。

      首先定义顺序表接口。SequenList.java。

//定义线性表接口
public interface SequneList{

    //定义线性表长度
    public int size();

    //判断线性表是否为空
    public boolean isEmpty();

    //插入元素
    public void insert(int index,Object obj) throws Exception;

    //删除元素
    public  void  delete(int index) throws Exception;

    //获取指定位置的元素
    public Object get(int index) throws Exception;

}

后面是具体的实现。List.java。

public class List implements SequneList{

    //线性表最大长度
    final int defaultSize=100;
    //最大长度
    int maxSize;
    //当前长度
    int size;
    //创建对象数组
    Object[] listArray;

    public List(){
        init(defaultSize);
    }

    public List(int size){
        init(size);
    }

    //定义顺序表的初始化方法
    public void init(int size){
        maxSize=size;
        this.size=0;
        listArray=new Object[size];
    }

    //插入数据
    @Override
    public void insert(int index, Object obj) throws Exception {

        //检查线性表是否已满
        if(size==maxSize){
            throw new Exception ("顺序表已满，无法插入数据");
        }

        //检查插入位置是否合法
        if(index<0||index>size){
            throw new Exception("插入位置错误");
        }

        //移动元素
        for(int j=size-1;j>index;j--){
            listArray[j+1]=listArray[j];
        }

        listArray[index]=obj;
        size++;
    }

    @Override
    public boolean isEmpty() {
        return size==0;
    }

    public int size(){
        return size;
    }

    public Object get(int index) throws Exception{
        if(index<0||index>=size){
            throw new Exception("获取参数错误");
        }
        return listArray[index];
    }

    @Override
    public void delete(int index) throws Exception {
        if(isEmpty()){
            throw new Exception("顺序表为空，无法删除");
        }
        if(index<0||index>size-1){
            throw new Exception("参数错误");
        }
        //移动元素
        for (int j=index;j<size-1;j++){
            listArray[j]=listArray[j+1];
        }
        size--;
    }
}

class test{
    public static void main(String[] args){
        List list=new List();
        try{
            list.insert(0,100);
        }catch (Exception e){
            e.printStackTrace();
        }
    }
}

3、顺序表效率分析：

• 顺序表插入和删除一个元素的时间复杂度为O(n)。
• 顺序表支持随机访问，顺序表读取一个元素的时间复杂度为O(1)。因为我们是可以通过下标直接访问的，所以时间复杂度是固定的，和问题规模无关。

4、顺序表的优缺点：

• 顺序表的优点是：支持随机访问；空间利用率高（连续分配，不存在空间浪费）。
• 顺序表的缺点是：大小固定（一开始就要固定顺序表的最大长度）；插入和删除元素需要移动大量的数据。