C语言中有许多经典的算法,以下我列出了一些常见的经典算法,并为每个算法提供了一些解释。
1. 冒泡排序(Bubble Sort)
概述:冒泡排序是一种简单的排序算法,它通过重复遍历要排序的列表,比较相邻元素并交换顺序来实现排序。
#include <stdio.h> // 冒泡排序函数 void bubbleSort(int arr[], int n) { // 外层循环用于控制总的遍历次数 for (int i = 0; i < n - 1; i++) { // 内层循环用于比较相邻元素并进行交换 for (int j = 0; j < n - i - 1; j++) { if (arr[j] > arr[j + 1]) { // 如果前一个元素大于后一个元素,则交换 int temp = arr[j]; arr[j] = arr[j + 1]; arr[j + 1] = temp; } } } } int main() { int arr[] = {64, 34, 25, 12, 22, 11, 90}; int n = sizeof(arr) / sizeof(arr[0]); bubbleSort(arr, n); printf("排序后的数组: \n"); for (int i = 0; i < n; i++) { printf("%d ", arr[i]); } return 0; }
解释:冒泡排序的核心思想是每次遍历都将最大的元素“冒泡”到最后。外层循环控制遍历次数,内层循环负责交换相邻元素。交换条件是前面的元素大于后面的元素。
2. 选择排序(Selection Sort)
概述:选择排序是一种简单的排序算法,每次从未排序的部分中选择最小的元素,将其放在已排序部分的末尾。
#include <stdio.h> // 选择排序函数 void selectionSort(int arr[], int n) { for (int i = 0; i < n - 1; i++) { // 假设当前的第i个元素是最小的 int minIdx = i; // 找到未排序部分的最小元素 for (int j = i + 1; j < n; j++) { if (arr[j] < arr[minIdx]) { minIdx = j; } } // 交换最小元素和当前元素 int temp = arr[minIdx]; arr[minIdx] = arr[i]; arr[i] = temp; } } int main() { int arr[] = {64, 25, 12, 22, 11}; int n = sizeof(arr) / sizeof(arr[0]); selectionSort(arr, n); printf("排序后的数组: \n"); for (int i = 0; i < n; i++) { printf("%d ", arr[i]); } return 0; }
解释:选择排序的设计非常直观:从剩余的未排序部分中找到最小的元素,将它放到正确的位置。这个算法通过减少交换次数提升了效率。
3. 插入排序(Insertion Sort)
概述:插入排序的工作方式与整理扑克牌类似,每次将一个元素插入到已排序部分的适当位置。
#include <stdio.h> // 插入排序函数 void insertionSort(int arr[], int n) { for (int i = 1; i < n; i++) { int key = arr[i]; // 当前元素 int j = i - 1; // 移动大于当前元素的元素,给当前元素腾出位置 while (j >= 0 && arr[j] > key) { arr[j + 1] = arr[j]; j = j - 1; } arr[j + 1] = key; // 插入当前元素 } } int main() { int arr[] = {12, 11, 13, 5, 6}; int n = sizeof(arr) / sizeof(arr[0]); insertionSort(arr, n); printf("排序后的数组: \n"); for (int i = 0; i < n; i++) { printf("%d ", arr[i]); } return 0; }
解释:插入排序通过依次将元素插入到已排序部分的适当位置进行排序。设计上,它的优势是对于近乎排序的数组表现良好,时间复杂度较低。
4. 二分查找(Binary Search)
概述:二分查找是一种在有序数组中查找目标值的高效算法,时间复杂度为 O(log n)。
#include <stdio.h> // 二分查找函数 int binarySearch(int arr[], int left, int right, int target) { while (left <= right) { int mid = left + (right - left) / 2; // 检查中间值是否是目标值 if (arr[mid] == target) { return mid; } // 如果目标值较大,忽略左半部分 if (arr[mid] < target) { left = mid + 1; } // 如果目标值较小,忽略右半部分 else { right = mid - 1; } } // 如果找不到目标值,返回-1 return -1; } int main() { int arr[] = {2, 3, 4, 10, 40}; int n = sizeof(arr) / sizeof(arr[0]); int target = 10; int result = binarySearch(arr, 0, n - 1, target); if (result == -1) { printf("元素未找到\n"); } else { printf("元素在索引 %d 处\n", result); } return 0; }
解释:二分查找的核心思想是每次将搜索空间缩小一半。该算法要求数组必须是有序的,因此可以通过比较中间值与目标值来决定搜索方向。
5. 快速排序(Quick Sort)
概述:快速排序是一种分治算法,它通过选择一个基准元素将数组分成两个部分,然后分别排序。
#include <stdio.h> // 交换函数 void swap(int* a, int* b) { int temp = *a; *a = *b; *b = temp; } // 分区函数 int partition(int arr[], int low, int high) { int pivot = arr[high]; // 选择最右边的元素作为基准 int i = (low - 1); // 小于基准的元素索引 for (int j = low; j < high; j++) { // 如果当前元素小于基准 if (arr[j] < pivot) { i++; swap(&arr[i], &arr[j]); // 交换元素 } } swap(&arr[i + 1], &arr[high]); return (i + 1); // 返回基准的正确位置 } // 快速排序函数 void quickSort(int arr[], int low, int high) { if (low < high) { int pi = partition(arr, low, high); // 递归排序基准左右的子数组 quickSort(arr, low, pi - 1); quickSort(arr, pi + 1, high); } } int main() { int arr[] = {10, 7, 8, 9, 1, 5}; int n = sizeof(arr) / sizeof(arr[0]); quickSort(arr, 0, n - 1); printf("排序后的数组: \n"); for (int i = 0; i < n; i++) { printf("%d ", arr[i]); } return 0; }
解释:快速排序通过递归地分区和排序子数组来实现排序。基准选择和分区策略决定了其效率。快速排序平均情况下时间复杂度为 O(n log n),是非常高效的排序算法。
6. 归并排序(Merge Sort)
概述:归并排序是一种分治算法,它将数组分成更小的子数组,然后递归地合并这些子数组。
#include <stdio.h> // 合并两个子数组 void merge(int arr[], int l, int m, int r) { int i, j, k; int n1 = m - l + 1; int n2 = r - m; // 创建临时数组 int L[n1], R[n2]; // 拷贝数据到临时数组 L[] 和 R[] for (i = 0; i < n1; i++) { L[i] = arr[l + i]; } for (j = 0; j < n2; j++) { R[j] = arr[m + 1 + j]; } // 合并临时数组到原数组 i = 0; // 左子数组初始索引 j = 0; // 右子数组初始索引 k = l; // 合并后数组的初始索引 while (i < n1 && j < n2) { if (L[i] <= R[j]) { arr[k] = L[i]; i++; } else { arr[k] = R[j]; j++; } k++; } // 拷贝 L[] 中的剩余元素 while (i < n1) { arr[k] = L[i]; i++; k++; } // 拷贝 R[] 中的剩余元素 while (j < n2) { arr[k] = R[j]; j++; k++; } } // 归并排序函数 void mergeSort(int arr[], int l, int r) { if (l < r) { int m = l + (r - l) / 2; // 递归排序前后两部分 mergeSort(arr, l, m); mergeSort(arr, m + 1, r); // 合并排序后的数组 merge(arr, l, m, r); } } int main() { int arr[] = {12, 11, 13, 5, 6, 7}; int arr_size = sizeof(arr) / sizeof(arr[0]); printf("原始数组: \n"); for (int i = 0; i < arr_size; i++) { printf("%d ", arr[i]); } printf("\n"); mergeSort(arr, 0, arr_size - 1); printf("排序后的数组: \n"); for (int i = 0; i < arr_size; i++) { printf("%d ", arr[i]); } return 0; }
解释:归并排序通过递归地将数组分成更小的子数组,然后将这些子数组排序并合并。这是一种稳定的排序算法,时间复杂度为 O(n log n)。
7. 堆排序(Heap Sort)
概述:堆排序是一种基于堆数据结构的排序算法,堆是一棵完全二叉树,每个节点的值都不大于或不小于其子节点的值。
#include <stdio.h> // 堆调整函数 void heapify(int arr[], int n, int i) { int largest = i; // 将当前节点设为最大 int l = 2 * i + 1; // 左子节点 int r = 2 * i + 2; // 右子节点 // 如果左子节点比最大值大 if (l < n && arr[l] > arr[largest]) largest = l; // 如果右子节点比最大值大 if (r < n && arr[r] > arr[largest]) largest = r; // 如果最大值不是当前节点 if (largest != i) { int temp = arr[i]; arr[i] = arr[largest]; arr[largest] = temp; // 递归地对受影响的子树进行调整 heapify(arr, n, largest); } } // 堆排序函数 void heapSort(int arr[], int n) { // 构建初始堆 for (int i = n / 2 - 1; i >= 0; i--) heapify(arr, n, i); // 提取元素从堆中 for (int i = n - 1; i > 0; i--) { // 将当前根与数组末尾元素交换 int temp = arr[0]; arr[0] = arr[i]; arr[i] = temp; // 调整堆结构 heapify(arr, i, 0); } } int main() { int arr[] = {12, 11, 13, 5, 6, 7}; int n = sizeof(arr) / sizeof(arr[0]); heapSort(arr, n); printf("排序后的数组: \n"); for (int i = 0; i < n; i++) { printf("%d ", arr[i]); } return 0; }
解释:堆排序通过构建最大堆来对数组进行排序,时间复杂度为 O(n log n)。它是一种不稳定的排序算法,但具有很好的性能。
8. 二叉树遍历(Binary Tree Traversal)
概述:二叉树的遍历包括前序遍历、中序遍历和后序遍历。
#include <stdio.h> #include <stdlib.h> // 定义树节点结构 struct Node { int data; struct Node* left; struct Node* right; }; // 创建新节点 struct Node* newNode(int data) { struct Node* node = (struct Node*)malloc(sizeof(struct Node)); node->data = data; node->left = NULL; node->right = NULL; return node; } // 前序遍历 void preorder(struct Node* node) { if (node == NULL) return; printf("%d ", node->data); // 访问根节点 preorder(node->left); // 遍历左子树 preorder(node->right); // 遍历右子树 } // 中序遍历 void inorder(struct Node* node) { if (node == NULL) return; inorder(node->left); // 遍历左子树 printf("%d ", node->data); // 访问根节点 inorder(node->right); // 遍历右子树 } // 后序遍历 void postorder(struct Node* node) { if (node == NULL) return; postorder(node->left); // 遍历左子树 postorder(node->right); // 遍历右子树 printf("%d ", node->data); // 访问根节点 } int main() { struct Node* root = newNode(1); root->left = newNode(2); root->right = newNode(3); root->left->left = newNode(4); root->left->right = newNode(5); printf("前序遍历: "); preorder(root); printf("\n"); printf("中序遍历: "); inorder(root); printf("\n"); printf("后序遍历: "); postorder(root); printf("\n"); return 0; }
解释:二叉树的遍历是树结构算法中的重要部分,前序遍历是先访问根节点,中序遍历是先访问左子树,后序遍历是最后访问根节点。
9. Dijkstra算法(Dijkstra’s Algorithm)
概述:Dijkstra算法用于查找加权图中从一个顶点到其他顶点的最短路径。
#include <stdio.h> #include <limits.h> #define V 9 // 找到未处理的顶点中距离最小的顶点 int minDistance(int dist[], int sptSet[]) { int min = INT_MAX, min_index; for (int v = 0; v < V; v++) if (sptSet[v] == 0 && dist[v] <= min) min = dist[v], min_index = v; return min_index; } // 打印最终的最短距离 void printSolution(int dist[]) { printf("顶点 \t 距离源点\n"); for (int i = 0; i < V; i++) printf("%d \t\t %d\n", i, dist[i]); } // Dijkstra算法 void dijkstra(int graph[V][V], int src) { int dist[V]; int sptSet[V]; // 初始化距离和sptSet for ( int i = 0; i < V; i++) dist[i] = INT_MAX, sptSet[i] = 0; dist[src] = 0; for (int count = 0; count < V - 1; count++) { int u = minDistance(dist, sptSet); sptSet[u] = 1; for (int v = 0; v < V; v++) if (!sptSet[v] && graph[u][v] && dist[u] != INT_MAX && dist[u] + graph[u][v] < dist[v]) dist[v] = dist[u] + graph[u][v]; } printSolution(dist); } int main() { int graph[V][V] = {{0, 4, 0, 0, 0, 0, 0, 8, 0}, {4, 0, 8, 0, 0, 0, 0, 11, 0}, {0, 8, 0, 7, 0, 4, 0, 0, 2}, {0, 0, 7, 0, 9, 14, 0, 0, 0}, {0, 0, 0, 9, 0, 10, 0, 0, 0}, {0, 0, 4, 14, 10, 0, 2, 0, 0}, {0, 0, 0, 0, 0, 2, 0, 1, 6}, {8, 11, 0, 0, 0, 0, 1, 0, 7}, {0, 0, 2, 0, 0, 0, 6, 7, 0}}; dijkstra(graph, 0); return 0; }
解释:Dijkstra算法是一种贪心算法,用于找到从源点到所有其他顶点的最短路径。
10. 九九乘法表
概述:输出标准的九九乘法表。
#include <stdio.h> int main() { // 外层循环控制行数 for (int i = 1; i <= 9; i++) { // 内层循环控制每一行的列数 for (int j = 1; j <= i; j++) { printf("%d*%d=%d\t", j, i, i * j); // 输出乘法表达式和结果 } printf("\n"); // 换行 } return 0; }
解释:通过嵌套的两层循环来生成乘法表,外层循环控制行数,内层循环控制每一行的内容。我们只计算上三角部分的乘法表,所以内层循环的上限为 i。
11. 斐波那契数列(Fibonacci Sequence)
概述:斐波那契数列是这样一个序列:0, 1, 1, 2, 3, 5, 8, 13… 每个数都是前两个数之和。
#include <stdio.h> // 返回斐波那契数列中的第n个数 int fibonacci(int n) { if (n == 0) return 0; // 基本情况1:f(0) = 0 if (n == 1) return 1; // 基本情况2:f(1) = 1 return fibonacci(n - 1) + fibonacci(n - 2); // 递归定义 } int main() { int n; printf("输入要生成斐波那契数列的项数: "); scanf("%d", &n); for (int i = 0; i < n; i++) { printf("%d ", fibonacci(i)); // 输出斐波那契数列的每一项 } printf("\n"); return 0; }
解释:通过递归定义斐波那契数列。递归函数 fibonacci 通过调用自身计算每一个数列的值。
12. 判断质数(Prime Number Check)
概述:判断一个给定的数字是否为质数。
#include <stdio.h> // 判断是否为质数的函数 int isPrime(int n) { if (n <= 1) return 0; // 1 或小于1的数不是质数 for (int i = 2; i * i <= n; i++) { if (n % i == 0) return 0; // 如果能被i整除,则不是质数 } return 1; // 否则是质数 } int main() { int n; printf("输入一个数字: "); scanf("%d", &n); if (isPrime(n)) printf("%d 是质数\n", n); else printf("%d 不是质数\n", n); return 0; }
解释:通过遍历从 2 到 √n 的所有数字,判断是否存在可以整除 n 的数字,如果存在,则 n 不是质数,否则是质数。
13. 求阶乘(Factorial)
概述:求给定数字的阶乘。
#include <stdio.h> // 计算n的阶乘 long long factorial(int n) { if (n == 0) return 1; // 0的阶乘是1 return n * factorial(n - 1); // 递归调用 } int main() { int n; printf("输入一个数字: "); scanf("%d", &n); printf("%d 的阶乘是 %lld\n", n, factorial(n)); return 0; }
解释:使用递归函数计算阶乘,递归的终止条件是 n == 0,这时返回1。否则,继续递归调用 n * factorial(n - 1)。
14. 最大公约数(GCD, Greatest Common Divisor)
概述:使用欧几里得算法求两个数的最大公约数。
#include <stdio.h> // 计算两个数的最大公约数 int gcd(int a, int b) { if (b == 0) return a; // 如果b为0,返回a return gcd(b, a % b); // 否则递归调用gcd(b, a % b) } int main() { int a, b; printf("输入两个数字: "); scanf("%d %d", &a, &b); printf("%d 和 %d 的最大公约数是 %d\n", a, b, gcd(a, b)); return 0; }
解释:欧几里得算法通过递归计算两个数的最大公约数,直到余数为0时返回当前的除数。
15. 最小公倍数(LCM, Least Common Multiple)
概述:通过最大公约数(GCD)计算两个数的最小公倍数。
#include <stdio.h> // 计算两个数的最大公约数 int gcd(int a, int b) { if (b == 0) return a; return gcd(b, a % b); } // 计算两个数的最小公倍数 int lcm(int a, int b) { return (a * b) / gcd(a, b); // lcm(a, b) = a * b / gcd(a, b) } int main() { int a, b; printf("输入两个数字: "); scanf("%d %d", &a, &b); printf("%d 和 %d 的最小公倍数是 %d\n", a, b, lcm(a, b)); return 0; }
解释:最小公倍数等于两个数的乘积除以它们的最大公约数。通过调用 gcd 函数来计算 lcm。
16. 数字反转(Reverse a Number)
概述:反转一个给定的数字。
#include <stdio.h> // 反转数字 int reverseNumber(int n) { int reversed = 0; while (n != 0) { reversed = reversed * 10 + n % 10; // 将当前数字的最后一位加到reversed n /= 10; // 去掉数字的最后一位 } return reversed; } int main() { int n; printf("输入一个数字: "); scanf("%d", &n); printf("反转后的数字是 %d\n", reverseNumber(n)); return 0; }
解释:通过将数字的最后一位依次添加到 reversed 来实现数字反转。
17. 阿姆斯特朗数(Armstrong Number)
概述:检查一个数是否为阿姆斯特朗数。一个 n 位的阿姆斯特朗数是指该数等于其各位数的 n 次方的和。
#include <stdio.h> #include <math.h> // 计算位数 int countDigits(int n) { int count = 0; while (n != 0) { count++; n /= 10; } return count; } // 判断是否为阿姆斯特朗数 int isArmstrong(int n) { int original = n; int sum = 0; int digits = countDigits(n); while (n != 0) { int digit = n % 10; sum += pow(digit, digits); // 计算每个位的次方和 n /= 10; } return sum == original; // 判断是否为阿姆斯特朗数 } int main() { int n; printf("输入一个数字: "); scanf("%d", &n); if (isArmstrong(n)) printf("%d 是阿姆斯特朗数\n", n); else printf("%d 不是阿姆斯特朗数\n", n); return 0; }
解释:通过逐位计算每个位的 n 次方和,判断该数字是否为阿姆斯特朗数。
18. 金字塔图案编程(Pyramid Pattern)
概述:根据给定的行数输出金字塔图案。
#include <stdio.h> int main() { int rows; printf("输入金字塔的行数: "); scanf("%d", &rows); for (int i = 1; i <= rows; i++) { // 输出前面的空格 for (int j = 1; j <= rows - i; j++) { printf(" "); } // 输出金字塔的星号 for (int j = 1; j <= 2 * i - 1; j++) { printf("*"); } printf("\n"); // 换行 } return 0; }
解释:这个程序通过两层嵌套循环实现。外层循环控制行数,内层第一个循环输出空格,第二个循环输出星号,构成金字塔图案。
19. 鸡兔同笼问题
概述:鸡兔同笼问题是中国古代的一个数学题目:假设有若干只鸡和兔子在一个笼子里,已知总的头数和脚数,求鸡和兔子各有多少只。
#include <stdio.h> int main() { int heads, legs; printf("输入总头数和脚数: "); scanf("%d %d", &heads, &legs); // x表示鸡的数量,y表示兔子的数量 // 鸡有2条腿,兔子有4条腿,因此: // x + y = heads (总头数) // 2x + 4y = legs (总脚数) // 解方程组得: int x = (4 * heads - legs) / 2; // 鸡的数量 int y = heads - x; // 兔子的数量 // 检查是否有解 if (x >= 0 && y >= 0 && (2 * x + 4 * y == legs)) { printf("鸡的数量: %d, 兔子的数量: %d\n", x, y); } else { printf("无解\n"); } return 0; }
解释:通过列出方程组 x + y = heads 和 2x + 4y = legs 来解出鸡和兔子的数量。如果解出的数量为正且符合脚数要求,输出结果,否则输出 “无解”。
20. 打印倒金字塔图案(Inverted Pyramid Pattern)
概述:根据给定的行数输出倒金字塔图案。
#include <stdio.h> int main() { int rows; printf("输入倒金字塔的行数: "); scanf("%d", &rows); for (int i = rows; i >= 1; i--) { // 输出前面的空格 for (int j = 1; j <= rows - i; j++) { printf(" "); } // 输出倒金字塔的星号 for (int j = 1; j <= 2 * i - 1; j++) { printf("*"); } printf("\n"); // 换行 } return 0; }
解释:这个程序通过控制星号和空格的数量实现倒金字塔图案。与正金字塔类似,区别在于外层循环从最大行数开始递减。
21. 简单的加密算法(Caesar Cipher)
概述:Caesar Cipher 是一种简单的加密算法,通过将字母按字母表顺序偏移固定的位数进行加密。
#include <stdio.h> #include <string.h> void encrypt(char text[], int shift) { for (int i = 0; i < strlen(text); i++) { char c = text[i]; if (c >= 'a' && c <= 'z') { text[i] = (c - 'a' + shift) % 26 + 'a'; // 对小写字母加密 } else if (c >= 'A' && c <= 'Z') { text[i] = (c - 'A' + shift) % 26 + 'A'; // 对大写字母加密 } } } int main() { char text[100]; int shift; printf("输入要加密的文本: "); gets(text); printf("输入偏移量: "); scanf("%d", &shift); encrypt(text, shift); printf("加密后的文本: %s\n", text); return 0; }
解释:Caesar Cipher 是一种古老的加密算法,将每个字母按字母表顺序偏移固定的位数,非字母字符保持不变。
22. 计算水仙花数(Armstrong Number for 3-digit numbers)
概述:水仙花数是指一个三位数,其各个位数的立方和等于该数本身。
#include <stdio.h> #include <math.h> int isArmstrong(int n) { int original = n; int sum = 0; while (n != 0) { int digit = n % 10; sum += pow(digit, 3); // 立方和 n /= 10; } return sum == original; } int main() { for (int i = 100; i < 1000; i++) { if (isArmstrong(i)) { printf("%d 是水仙花数\n", i); } } return 0; }
解释:程序通过逐个检查三位数,并判断是否满足水仙花数的条件,即其各位数字的立方和等于该数本身。
23. 判断日期是该年的第几天
概述:输入一个日期(年、月、日),判断这一天是该年的第几天。
#include <stdio.h> // 判断是否为闰年 int isLeapYear(int year) { return (year % 4 == 0 && year % 100 != 0) || (year % 400 == 0); } // 计算该日期为一年中的第几天 int dayOfYear(int year, int month, int day) { int daysInMonth[] = {31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31}; if (isLeapYear(year)) { daysInMonth[1] = 29; // 闰年2月有29天 } int dayOfYear = 0; for (int i = 0; i < month - 1; i++) { dayOfYear += daysInMonth[i]; // 累加前几个月的天数 } dayOfYear += day; // 加上当前月的天数 return dayOfYear; } int main() { int year, month, day; printf("请输入年份: "); scanf("%d", &year); printf("请输入月份: "); scanf("%d", &month); printf("请输入日期: "); scanf("%d", &day); int result = dayOfYear(year, month, day); printf("这一天是该年的第 %d 天\n", result); return 0; }
解释:
程序通过判断是否为闰年,并累加每个月的天数,最终计算出某一天是该年的第几天。闰年时,2月份有29天,其余年份2月份为28天。
24. 判断素数(Prime Number)
概述:判断一个整数是否为素数。
#include <stdio.h> // 判断是否为素数 int isPrime(int n) { if (n <= 1) { return 0; // 1 和小于1的数不是素数 } for (int i = 2; i * i <= n; i++) { if (n % i == 0) { return 0; // 能被其他数整除的数不是素数 } } return 1; // 素数 } int main() { int num; printf("请输入一个整数: "); scanf("%d", &num); if (isPrime(num)) { printf("%d 是素数\n", num); } else { printf("%d 不是素数\n", num); } return 0; }
解释:
素数是指只能被1和自身整除的数。通过遍历2到平方根范围内的整数,判断是否存在能整除输入数的情况,若存在则该数不是素数。
25. 判断闰年(Leap Year)
概述:判断输入的年份是否为闰年。
#include <stdio.h> // 判断是否为闰年 int isLeapYear(int year) { if ((year % 4 == 0 && year % 100 != 0) || (year % 400 == 0)) { return 1; // 闰年 } return 0; // 平年 } int main() { int year; printf("请输入年份: "); scanf("%d", &year); if (isLeapYear(year)) { printf("%d 是闰年\n", year); } else { printf("%d 不是闰年\n", year); } return 0; }
解释:
闰年判断规则:能被4整除但不能被100整除,或者能被400整除的年份为闰年。
26. 打印菱形图案(Diamond Pattern)
概述:根据输入的行数,输出一个菱形图案。
#include <stdio.h> int main() { int n; printf("请输入菱形的行数: "); scanf("%d", &n); // 打印上半部分 for (int i = 1; i <= n; i++) { for (int j = 1; j <= n - i; j++) { printf(" "); } for (int j = 1; j <= 2 * i - 1; j++) { printf("*"); } printf("\n"); } // 打印下半部分 for (int i = n - 1; i >= 1; i--) { for (int j = 1; j <= n - i; j++) { printf(" "); } for (int j = 1; j <= 2 * i - 1; j++) { printf("*"); } printf("\n"); } return 0; }
解释:
通过两段循环实现菱形图案。上半部分为正金字塔,下半部分为倒金字塔。
27. 鸡兔同笼(扩展版)
概述:解决鸡兔同笼问题,给出头和脚的数量,求鸡和兔的数量,并考虑无解的情况。
#include <stdio.h> int main() { int heads, legs; printf("请输入总头数: "); scanf("%d", &heads); printf("请输入总脚数: "); scanf("%d", &legs); // 通过方程计算鸡和兔的数量 int rabbits = (legs - 2 * heads) / 2; int chickens = heads - rabbits; // 检查 解的合法性 if (rabbits >= 0 && chickens >= 0 && 2 * chickens + 4 * rabbits == legs) { printf("鸡的数量: %d, 兔的数量: %d\n", chickens, rabbits); } else { printf("无解\n"); } return 0; }
解释:
通过设立方程 2 * chickens + 4 * rabbits = legs,求出兔和鸡的数量,并验证解的合理性。
黑客/网络安全学习路线
对于从来没有接触过黑客/网络安全的同学,目前网络安全、信息安全也是计算机大学生毕业薪资相对较高的学科。
大白也帮大家准备了详细的学习成长路线图。可以说是最科学最系统的学习路线,大家跟着这个大的方向学习准没问题。
这也是耗费了大白近四个月的时间,吐血整理,文章非常非常长,觉得有用的话,希望粉丝朋友帮忙点个**「分享」「收藏」「在看」「赞」**
网络安全/渗透测试法律法规必知必会****
今天大白就帮想学黑客/网络安全技术的朋友们入门必须先了解法律法律。
【网络安全零基础入门必知必会】什么是黑客、白客、红客、极客、脚本小子?(02)
【网络安全零基础入门必知必会】网络安全专业术语全面解析(05)
【网络安全入门必知必会】《中华人民共和国网络安全法》(06)
【网络安全零基础入门必知必会】《计算机信息系统安全保护条例》(07)
【网络安全零基础入门必知必会】《中国计算机信息网络国际联网管理暂行规定》(08)
【网络安全零基础入门必知必会】《计算机信息网络国际互联网安全保护管理办法》(09)
【网络安全零基础入门必知必会】《互联网信息服务管理办法》(10)
【网络安全零基础入门必知必会】《计算机信息系统安全专用产品检测和销售许可证管理办法》(11)
【网络安全零基础入门必知必会】《通信网络安全防护管理办法》(12)
【网络安全零基础入门必知必会】《中华人民共和国国家安全法》(13)
【网络安全零基础入门必知必会】《中华人民共和国数据安全法》(14)
【网络安全零基础入门必知必会】《中华人民共和国个人信息保护法》(15)
【网络安全零基础入门必知必会】《网络产品安全漏洞管理规定》(16)
网络安全/渗透测试linux入门必知必会
【网络安全零基础入门必知必会】什么是Linux?Linux系统的组成与版本?什么是命令(01)
【网络安全零基础入门必知必会】VMware下载安装,使用VMware新建虚拟机,远程管理工具(02)
【网络安全零基础入门必知必会】VMware常用操作指南(非常详细)零基础入门到精通,收藏这一篇就够了(03)
【网络安全零基础入门必知必会】CentOS7安装流程步骤教程(非常详细)零基入门到精通,收藏这一篇就够了(04)
【网络安全零基础入门必知必会】Linux系统目录结构详细介绍(05)
【网络安全零基础入门必知必会】Linux 命令大全(非常详细)零基础入门到精通,收藏这一篇就够了(06)
【网络安全零基础入门必知必会】linux安全加固(非常详细)零基础入门到精通,收藏这一篇就够了(07)
网络安全/渗透测试****计算机网络入门必知必会****
【网络安全零基础入门必知必会】TCP/IP协议深入解析(非常详细)零基础入门到精通,收藏这一篇就够了(01)
【网络安全零基础入门必知必会】什么是HTTP数据包&Http数据包分析(非常详细)零基础入门到精通,收藏这一篇就够了(02)
【网络安全零基础入门必知必会】计算机网络—子网划分、子网掩码和网关(非常详细)零基础入门到精通,收藏这一篇就够了(03)
网络安全/渗透测试入门之HTML入门必知必会
【网络安全零基础入门必知必会】什么是HTML&HTML基本结构&HTML基本使用(非常详细)零基础入门到精通,收藏这一篇就够了1
【网络安全零基础入门必知必会】VScode、PhpStorm的安装使用、Php的环境配置,零基础入门到精通,收藏这一篇就够了2
【网络安全零基础入门必知必会】HTML之编写登录和文件上传(非常详细)零基础入门到精通,收藏这一篇就够了3
网络安全/渗透测试入门之Javascript入门必知必会
【网络安全零基础入门必知必会】Javascript语法基础(非常详细)零基础入门到精通,收藏这一篇就够了(01)
【网络安全零基础入门必知必会】Javascript实现Post请求、Ajax请求、输出数据到页面、实现前进后退、文件上传(02)
网络安全/渗透测试入门之Shell入门必知必会
【网络安全零基础入门必知必会】Shell编程基础入门(非常详细)零基础入门到精通,收藏这一篇就够了(第七章)
网络安全/渗透测试入门之PHP入门必知必会
【网络安全零基础入门】PHP环境搭建、安装Apache、安装与配置MySQL(非常详细)零基础入门到精通,收藏这一篇就够(01)
【网络安全零基础入门】PHP基础语法(非常详细)零基础入门到精通,收藏这一篇就够了(02)
【网络安全零基础入门必知必会】PHP+Bootstrap实现表单校验功能、PHP+MYSQL实现简单的用户注册登录功能(03)
网络安全/渗透测试入门之MySQL入门必知必会
【网络安全零基础入门必知必会】MySQL数据库基础知识/安装(非常详细)零基础入门到精通,收藏这一篇就够了(01)
【网络安全零基础入门必知必会】SQL语言入门(非常详细)零基础入门到精通,收藏这一篇就够了(02)
【网络安全零基础入门必知必会】MySQL函数使用大全(非常详细)零基础入门到精通,收藏这一篇就够了(03)
【网络安全零基础入门必知必会】MySQL多表查询语法(非常详细)零基础入门到精通,收藏这一篇就够了(04)
****网络安全/渗透测试入门之Python入门必知必会
【网络安全零基础入门必知必会】之Python+Pycharm安装保姆级教程,Python环境配置使用指南,收藏这一篇就够了【1】
【网络安全零基础入门必知必会】之Python编程入门教程(非常详细)零基础入门到精通,收藏这一篇就够了(2)
python入门教程python开发基本流程控制if … else
python入门教程之python开发可变和不可变数据类型和hash
【网络安全零基础入门必知必会】之10个python爬虫入门实例(非常详细)零基础入门到精通,收藏这一篇就够了(3)
****网络安全/渗透测试入门之SQL注入入门必知必会
【网络安全渗透测试零基础入门必知必会】之初识SQL注入(非常详细)零基础入门到精通,收藏这一篇就够了(1)
【网络安全渗透测试零基础入门必知必会】之SQL手工注入基础语法&工具介绍(2)
【网络安全渗透测试零基础入门必知必会】之SQL注入实战(非常详细)零基础入门到精通,收藏这一篇就够了(3)
【网络安全渗透测试零基础入门必知必会】之SQLmap安装&实战(非常详细)零基础入门到精通,收藏这一篇就够了(4)
【网络安全渗透测试零基础入门必知必会】之SQL防御(非常详细)零基础入门到精通,收藏这一篇就够了(4)
****网络安全/渗透测试入门之XSS攻击入门必知必会
【网络安全渗透测试零基础入门必知必会】之XSS攻击基本概念和原理介绍(非常详细)零基础入门到精通,收藏这一篇就够了(1)
网络安全渗透测试零基础入门必知必会】之XSS攻击获取用户cookie和用户密码(实战演示)零基础入门到精通收藏这一篇就够了(2)
【网络安全渗透测试零基础入门必知必会】之XSS攻击获取键盘记录(实战演示)零基础入门到精通收藏这一篇就够了(3)
【网络安全渗透测试零基础入门必知必会】之xss-platform平台的入门搭建(非常详细)零基础入门到精通,收藏这一篇就够了4
【网络安全渗透测试入门】之XSS漏洞检测、利用和防御机制XSS游戏(非常详细)零基础入门到精通,收藏这一篇就够了5
****网络安全/渗透测试入门文件上传攻击与防御入门必知必会
【网络安全渗透测试零基础入门必知必会】之什么是文件包含漏洞&分类(非常详细)零基础入门到精通,收藏这一篇就够了1
【网络安全渗透测试零基础入门必知必会】之cve实际漏洞案例解析(非常详细)零基础入门到精通, 收藏这一篇就够了2
【网络安全渗透测试零基础入门必知必会】之PHP伪协议精讲(文件包含漏洞)零基础入门到精通,收藏这一篇就够了3
【网络安全渗透测试零基础入门必知必会】之如何搭建 DVWA 靶场保姆级教程(非常详细)零基础入门到精通,收藏这一篇就够了4
【网络安全渗透测试零基础入门必知必会】之Web漏洞-文件包含漏洞超详细全解(附实例)5
【网络安全渗透测试零基础入门必知必会】之文件上传漏洞修复方案6
****网络安全/渗透测试入门CSRF渗透与防御必知必会
【网络安全渗透测试零基础入门必知必会】之CSRF漏洞概述和原理(非常详细)零基础入门到精通, 收藏这一篇就够了1
【网络安全渗透测试零基础入门必知必会】之CSRF攻击的危害&分类(非常详细)零基础入门到精通, 收藏这一篇就够了2
【网络安全渗透测试零基础入门必知必会】之XSS与CSRF的区别(非常详细)零基础入门到精通, 收藏这一篇就够了3
【网络安全渗透测试零基础入门必知必会】之CSRF漏洞挖掘与自动化工具(非常详细)零基础入门到精通,收藏这一篇就够了4
【网络安全渗透测试零基础入门必知必会】之CSRF请求伪造&Referer同源&置空&配合XSS&Token值校验&复用删除5
****网络安全/渗透测试入门SSRF渗透与防御必知必会
【网络安全渗透测试零基础入门必知必会】之SSRF漏洞概述及原理(非常详细)零基础入门到精通,收藏这一篇就够了 1
【网络安全渗透测试零基础入门必知必会】之SSRF相关函数和协议(非常详细)零基础入门到精通,收藏这一篇就够了2
【网络安全渗透测试零基础入门必知必会】之SSRF漏洞原理攻击与防御(非常详细)零基础入门到精通,收藏这一篇就够了3**
**
****网络安全/渗透测试入门XXE渗透与防御必知必会
【网络安全渗透测试零基础入门必知必会】之XML外部实体注入(非常详细)零基础入门到精通,收藏这一篇就够了1
网络安全渗透测试零基础入门必知必会】之XXE的攻击与危害(非常详细)零基础入门到精通,收藏这一篇就够了2
【网络安全渗透测试零基础入门必知必会】之XXE漏洞漏洞及利用方法解析(非常详细)零基础入门到精通,收藏这一篇就够了3
【网络安全渗透测试零基础入门必知必会】之微信XXE安全漏洞处理(非常详细)零基础入门到精通,收藏这一篇就够了4
****网络安全/渗透测试入门远程代码执行渗透与防御必知必会
【网络安全渗透测试零基础入门必知必会】之远程代码执行原理介绍(非常详细)零基础入门到精通,收藏这一篇就够了1
【网络安全零基础入门必知必会】之CVE-2021-4034漏洞原理解析(非常详细)零基础入门到精通,收藏这一篇就够了2
【网络安全零基础入门必知必会】之PHP远程命令执行与代码执行原理利用与常见绕过总结3
【网络安全零基础入门必知必会】之WEB安全渗透测试-pikachu&DVWA靶场搭建教程,零基础入门到精通,收藏这一篇就够了4
****网络安全/渗透测试入门反序列化渗透与防御必知必会
【网络安全零基础入门必知必会】之什么是PHP对象反序列化操作(非常详细)零基础入门到精通,收藏这一篇就够了1
【网络安全零基础渗透测试入门必知必会】之php反序列化漏洞原理解析、如何防御此漏洞?如何利用此漏洞?2
【网络安全渗透测试零基础入门必知必会】之Java 反序列化漏洞(非常详细)零基础入门到精通,收藏这一篇就够了3
【网络安全渗透测试零基础入门必知必会】之Java反序列化漏洞及实例解析(非常详细)零基础入门到精通,收藏这一篇就够了4
【网络安全渗透测试零基础入门必知必会】之CTF题目解析Java代码审计中的反序列化漏洞,以及其他漏洞的组合利用5
网络安全/渗透测试**入门逻辑漏洞必知必会**
【网络安全渗透测试零基础入门必知必会】之一文带你0基础挖到逻辑漏洞(非常详细)零基础入门到精通,收藏这一篇就够了
网络安全/渗透测试入门暴力猜解与防御必知必会
【网络安全渗透测试零基础入门必知必会】之密码安全概述(非常详细)零基础入门到精通,收藏这一篇就够了1
【网络安全渗透测试零基础入门必知必会】之什么样的密码是不安全的?(非常详细)零基础入门到精通,收藏这一篇就够了2
【网络安全渗透测试零基础入门必知必会】之密码猜解思路(非常详细)零基础入门到精通,收藏这一篇就够了
【网络安全渗透测试零基础入门必知必会】之利用Python暴力破解邻居家WiFi密码、压缩包密码,收藏这一篇就够了4
【网络安全渗透测试零基础入门必知必会】之BurpSuite密码爆破实例演示,零基础入门到精通,收藏这一篇就够了5
【网络安全渗透测试零基础入门必知必会】之Hydra密码爆破工具使用教程图文教程,零基础入门到精通,收藏这一篇就够了
【网络安全渗透测试零基础入门必知必会】之暴力破解medusa,零基础入门到精通,收藏这一篇就够了7
【网络安全渗透测试零基础入门必知必会】之Metasploit抓取密码,零基础入门到精通,收藏这一篇就够了8
****网络安全/渗透测试入门掌握Redis未授权访问漏洞必知必会
【网络安全渗透测试零基础入门必知必会】之Redis未授权访问漏洞,零基础入门到精通,收藏这一篇就够了
【网络安全渗透测试零基础入门必知必会】之Redis服务器被攻击后该如何安全加固,零基础入门到精通,收藏这一篇就够了**
**
网络安全/渗透测试入门掌握**ARP渗透与防御关必知必会**
【网络安全渗透测试零基础入门必知必会】之ARP攻击原理解析,零基础入门到精通,收藏这一篇就够了
【网络安全渗透测试零基础入门必知必会】之ARP流量分析,零基础入门到精通,收藏这一篇就够了
【网络安全渗透测试零基础入门必知必会】之ARP防御策略与实践指南,零基础入门到精通,收藏这一篇就够了
网络安全/渗透测试入门掌握系统权限提升渗透与防御关****必知必会
【网络安全渗透测试零基础入门必知必会】之Windows提权常用命令,零基础入门到精通,收藏这一篇就够了
【网络安全渗透测试零基础入门必知必会】之Windows权限提升实战,零基础入门到精通,收藏这一篇就够了
【网络安全渗透测试零基础入门必知必会】之linux 提权(非常详细)零基础入门到精通,收藏这一篇就够了
网络安全/渗透测试入门掌握Dos与DDos渗透与防御相关****必知必会
【网络安全渗透测试零基础入门必知必会】之DoS与DDoS攻击原理(非常详细)零基础入门到精通,收藏这一篇就够了
【网络安全渗透测试零基础入门必知必会】之Syn-Flood攻击原理解析(非常详细)零基础入门到精通,收藏这一篇就够了
【网络安全渗透测试零基础入门必知必会】之IP源地址欺骗与dos攻击,零基础入门到精通,收藏这一篇就够了
【网络安全渗透测试零基础入门必知必会】之SNMP放大攻击原理及实战演示,零基础入门到精通,收藏这一篇就够了
【网络安全渗透测试零基础入门必知必会】之NTP放大攻击原理,零基础入门到精通,收藏这一篇就够了
【网络安全渗透测试零基础入门必知必会】之什么是CC攻击?CC攻击怎么防御?,零基础入门到精通,收藏这一篇就够了
【网络安全渗透测试零基础入门必知必会】之如何防御DDOS的攻击?零基础入门到精通,收藏这一篇就够了
网络安全/渗透测试入门掌握无线网络安全渗透与防御相关****必知必会
【网络安全渗透测试零基础入门必知必会】之Aircrack-ng详细使用安装教程,零基础入门到精通,收藏这一篇就够了
【网络安全渗透测试零基础入门必知必会】之aircrack-ng破解wifi密码(非常详细)零基础入门到精通,收藏这一篇就够了
【网络安全渗透测试零基础入门必知必会】之WEB渗透近源攻击,零基础入门到精通,收藏这一篇就够了
【网络安全渗透测试零基础入门必知必会】之无线渗透|Wi-Fi渗透思路,零基础入门到精通,收藏这一篇就够了
【网络安全渗透测试零基础入门必知必会】之渗透WEP新思路Hirte原理解析,零基础入门到精通,收藏这一篇就够了
【网络安全渗透测试零基础入门必知必会】之WPS的漏洞原理解析,零基础入门到精通,收藏这一篇就够了
网络安全/渗透测试入门掌握木马免杀问题与防御********必知必会
【网络安全渗透测试零基础入门必知必会】之Metasploit – 木马生成原理和方法,零基础入门到精通,收藏这篇就够了
【网络安全渗透测试零基础入门必知必会】之MSF使用教程永恒之蓝漏洞扫描与利用,收藏这一篇就够了
网络安全/渗透测试入门掌握Vulnhub靶场实战********必知必会
【网络安全渗透测试零基础入门必知必会】之Vulnhub靶机Prime使用指南,零基础入门到精通,收藏这一篇就够了
【网络安全渗透测试零基础入门必知必会】之Vulnhub靶场Breach1.0解析,零基础入门到精通,收藏这一篇就够了
【网络安全渗透测试零基础入门必知必会】之vulnhub靶场之DC-9,零基础入门到精通,收藏这一篇就够了
【网络安全渗透测试零基础入门必知必会】之Vulnhub靶机Kioptrix level-4 多种姿势渗透详解,收藏这一篇就够了
【网络安全渗透测试零基础入门必知必会】之Vulnhub靶场PWNOS: 2.0 多种渗透方法,收藏这一篇就够了
网络安全/渗透测试入门掌握社会工程学必知必会
【网络安全渗透测试零基础入门必知必会】之什么是社会工程学?定义、类型、攻击技术,收藏这一篇就够了
【网络安全渗透测试零基础入门必知必会】之社会工程学之香农-韦弗模式,收藏这一篇就够了
【网络安全渗透测试零基础入门必知必会】之社工学smcr通信模型,收藏这一篇就够了
【网络安全渗透测试零基础入门必知必会】之社会工程学之社工步骤整理(附相应工具下载)收藏这一篇就够了
网络安全/渗透测试入门掌握********渗透测试工具使用******必知必会**
2024版最新Kali Linux操作系统安装使用教程(非常详细)零基础入门到精通,收藏这一篇就够了
【网络安全渗透测试零基础入门必知必会】之渗透测试工具大全之Nmap安装使用命令指南,零基础入门到精通,收藏这一篇就够了
2024版最新AWVS安装使用教程(非常详细)零基础入门到精通,收藏这一篇就够了
2024版最新burpsuite安装使用教程(非常详细)零基础入门到精通,收藏这一篇就够了
2024版最新owasp_zap安装使用教程(非常详细)零基础入门到精通,收藏这一篇就够了
2024版最新Sqlmap安装使用教程(非常详细)零基础入门到精通,收藏这一篇就够了
2024版最新Metasploit安装使用教程(非常详细)零基础入门到精通,收藏这一篇就够了
2024版最新Nessus下载安装激活使用教程(非常详细)零基础入门到精通,收藏这一篇就够了
2024版最新Wireshark安装使用教程(非常详细)零基础入门到精通,收藏这一篇就够了
觉得有用的话,希望粉丝朋友帮大白点个**「分享」「收藏」「在看」「赞」**

黑客/网络安全学习包


资料目录
-
成长路线图&学习规划
-
配套视频教程
-
SRC&黑客文籍
-
护网行动资料
-
黑客必读书单
-
面试题合集
因篇幅有限,仅展示部分资料,需要点击下方链接即可前往获取
优快云大礼包:《黑客&网络安全入门&进阶学习资源包》免费分享
1.成长路线图&学习规划
要学习一门新的技术,作为新手一定要先学习成长路线图,方向不对,努力白费。
对于从来没有接触过网络安全的同学,我们帮你准备了详细的学习成长路线图&学习规划。可以说是最科学最系统的学习路线,大家跟着这个大的方向学习准没问题。

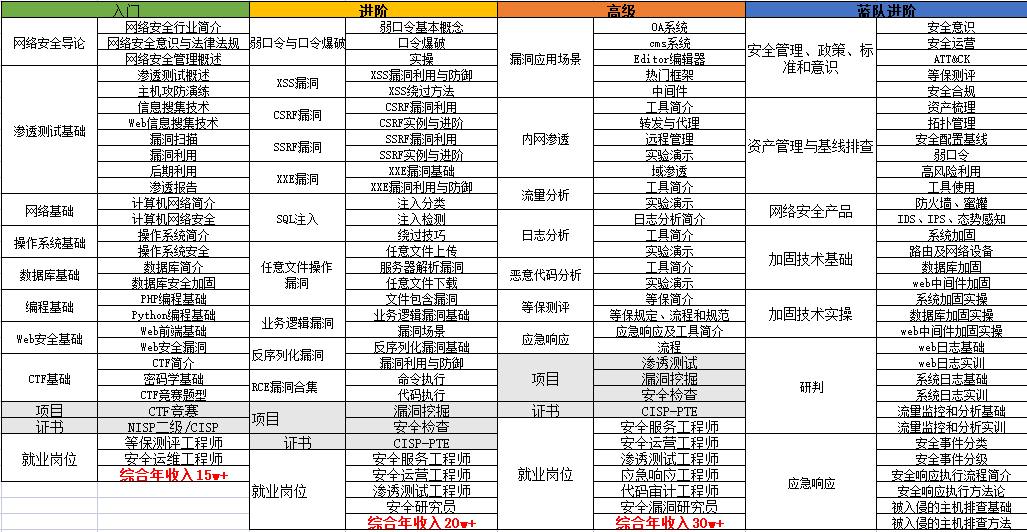
因篇幅有限,仅展示部分资料,需要点击下方链接即可前往获取
优快云大礼包:《黑客&网络安全入门&进阶学习资源包》免费分享
2.视频教程
很多朋友都不喜欢晦涩的文字,我也为大家准备了视频教程,其中一共有21个章节,每个章节都是当前板块的精华浓缩。
因篇幅有限,仅展示部分资料,需要点击下方链接即可前往获取
优快云大礼包:《黑客&网络安全入门&进阶学习资源包》免费分享
3.SRC&黑客文籍
大家最喜欢也是最关心的SRC技术文籍&黑客技术也有收录
SRC技术文籍:

黑客资料由于是敏感资源,这里不能直接展示哦!
4.护网行动资料
其中关于HW护网行动,也准备了对应的资料,这些内容可相当于比赛的金手指!
5.黑客必读书单
**

**
6.面试题合集
当你自学到这里,你就要开始思考找工作的事情了,而工作绕不开的就是真题和面试题。
更多内容为防止和谐,可以扫描获取~

因篇幅有限,仅展示部分资料,需要点击下方链接即可前往获取

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








