动态规划(Dynamic Programming)与贪心算法(Greedy Algorithm)

动态规划算法(Dynamic Programming)

动态规划问题的属性

  动态规划问题一般有两个性质。

性质一：最优子结构性质，即问题实例(关于问题实例，举个例子，排序是问题，输入一串具体的待排序的数就是问题实例)的最优解包含子问题的最优解。也就是说我们的问题可以抽象出父问题关于子问题的递推关系式(dp的重点)。

  但是仅有性质一，我们完全可以用递归法来解决。性质二的出现引出了动态规划算法。

性质二：重叠子问题性质，即根据性质一得到的递推关系式，用递归法解决，存在很多重复的子问题被反复计算。

  针对性质二，我们可以利用备忘录法，即存储计算过的子问题，下次碰到就不再计算。但是存储计算过的子问题，会额外增加存储空间的开销。因此引出了自底向上的动态规划算法，自底向上的意思是，我们先从最简单的子问题开始求解，引出更复杂的子问题的解，最终求出问题实例的解。

  设计优秀的动态规划算法，意识十分重要，其重点是，是否能找到合适的父问题关于子问题的递推关系式。一些问题的动态规划解法，并不能直接求出最终的解，而是求一个中间过程解，通过中间过程解在设计求出最终解，例如下面的最长公共子序列问题。

应用实例：最长公共子序列问题(Longest Common Subsequence, LCS)

问题描述：
  求出X，Y的一个最长公共子序列
输入：
  $X：A,B,C,B,D,A,B$
  $Y：B,D,C,A,B,A$
输出：
  $BDAB$ 或$BCAB$ 或 $BCBA$

分析：
  暴力法，设$X$的长度是$m$，$Y$的长度是$n$，找出$X$的所有子序列，时间复杂度$O(2^m)$，在$Y$中查找是否有对应的子序列，时间复杂度$O(n\cdot 2^m)$，指数阶时间复杂度速度很慢。

  设$X$的长度是$m$，$Y$的长度是$n$，令$C[i,j]$表示，截取$X$的索引从1到$i$，同时截取$Y$的索引从1到$j$的子序列的最长公共子序列的长度(这是一个中间过程解)，我们并没有一开始就定义最长子序列是什么，而是计算最长子序列的长度，最后通过回溯法重建最长子序列。这样我们就不难得到递推表达式：$$C[i,j]=\{\begin{array}{ll}C[i-1,j-1]+1& ifX[i]=Y[j]\\ max(C[i-1,j],C[i,j-1])& ifX[i]\ne Y[j]\end{array}$$

计算最长公共子序列的长度的问题就满足上面的性质一，根据这个递推表达式，我们可以建立递归的方法来执行，但是不难发现，如果想要知道$C[i,j-1]$与$C[i-1,j]$的结果(假设$X[i]\ne Y[j-1]$， $X[i-1]\ne Y[j]$)，我们均需要求$C[i-1,j-1]$的结果，这就导致了$C[i-1,j-1]$需要被计算两次，计算最长公共子序列的长度的问题就满足上面的性质二，我们可以利用备忘录法，也就是判断$C[i-1,j-1]$在之前是否被计算，并保存计算结果，避免重复计算，但是这样就增加了保存计算结果的存储开销。

  下面就利用动态规划法来解决，动态规划法就是把执行顺序变成自底向上，所以我们优先要知道初始状态。这一问题中，我们需要知道的初始状态包括$C[0,j]$以及$C[i,0]$，即$X,Y$有一个为空的情况，不难推断出：$$\begin{gathered} C[i,0]=0 \\ C[0,j]=0 \end{gathered}$$

接下来我们就自底向上，循环求解，时间复杂度$O(mn)$，python示意代码如下：

# 初始化C[i,0], C[0,j] = 0
for j in range(1,n):
    for i in range(1,m):
        if X[i] == Y[j]:
            C[i,j] = C[i-1,j-1] + 1
        else:
            C[i,j] = max(C[i-1,j],C[i,j-1])

我们用下面的图来表示该算法执行步骤：

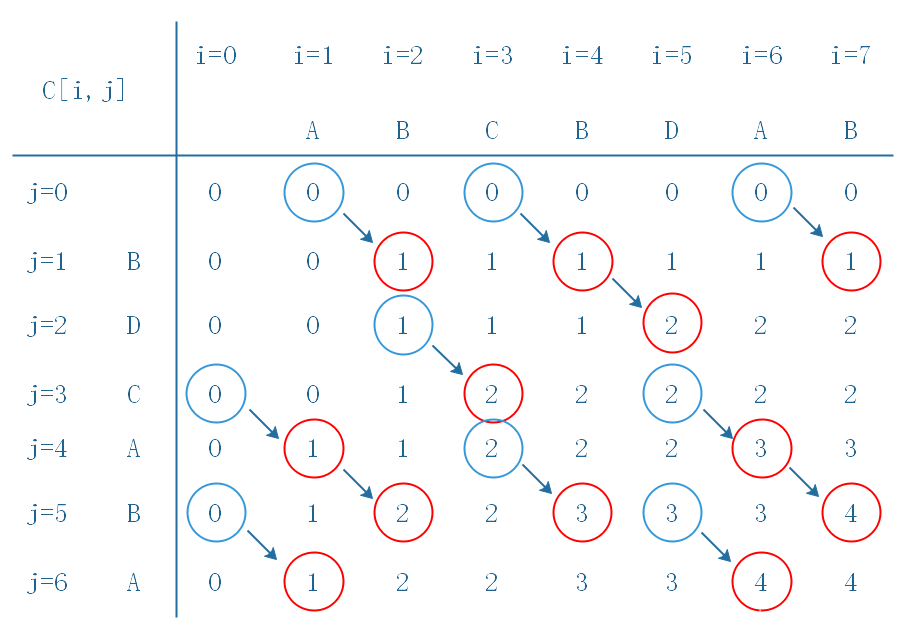
动态规划的问题在找到递推关系式后，我们都可以建立动态规划表(DP table)，如上图二维表，当然还可能是一维、三维等。上图两条垂直直线把图像分成四部分，右下部分就是$C[i,j]$的值，$i=0,1\dots m,j=0,1\dots n$，红圈就是发生$X[i]=Y[j]$的地方，对应的$C[i-1,j+1]$用篮圈表示，两者之间用箭头连接。

这样我们就求出来了最长公共自序列的长度，具体的最长公共子序列需要我们用回溯法构建，下图就是利用回溯法，回溯法的解空间就是上面的$C$，python示意代码如下。

import copy

rt = [] # 用于保存最终的输出
tmp = [] # 用于保存每一个LCS
X = ['A', 'B', 'C', 'B', 'D', 'A', 'B']
Y = ['B', 'D', 'C', 'A', 'B', 'A']

def backtrack(n, m, X, Y, rt, tmp, num):
    """
    一行一行的进行回溯
    
    Input
    ------
    n是当前第几层
    m表示当前层需要从第m列开始遍历
    X是最长公共子序列问题输入中的X
    Y是最长公共子序列问题输入中的Y
    rt用于保存最终的输出
    tmp用于保存每一个LCS
    num是确定的最长公共自序列长度
    """
    if (len(tmp) == num):
        rt.append(copy.deepcopy(tmp))  # 这里一定要用深拷贝!!!!
        return
    if (n == len(Y)):
        return
    for i in range(m, len(X)):
        if(X[i] == Y[n]):
            tmp.append(Y[n])
            backtrack(n+1, i+1, X, Y, rt, tmp, num)
            del(tmp[-1])  # python的列表删除操作
                # 用tmp = tmp[:-1]删除不成功，使用id(tmp)可以看出，
                # python认为tmp=tmp[:-1]生成的tmp是新生成的列表，和最初的tmp地址不一样。
        else:
            backtrack(n+1, i, X, Y, rt, tmp, num)

backtrack(0, 0, X, Y, rt, tmp, 4)
print(rt)

# 输出
# [['B', 'C', 'B', 'A'], ['B', 'C', 'A', 'B'], 
#  ['B', 'D', 'A', 'B'], ['B', 'D', 'A', 'B']]

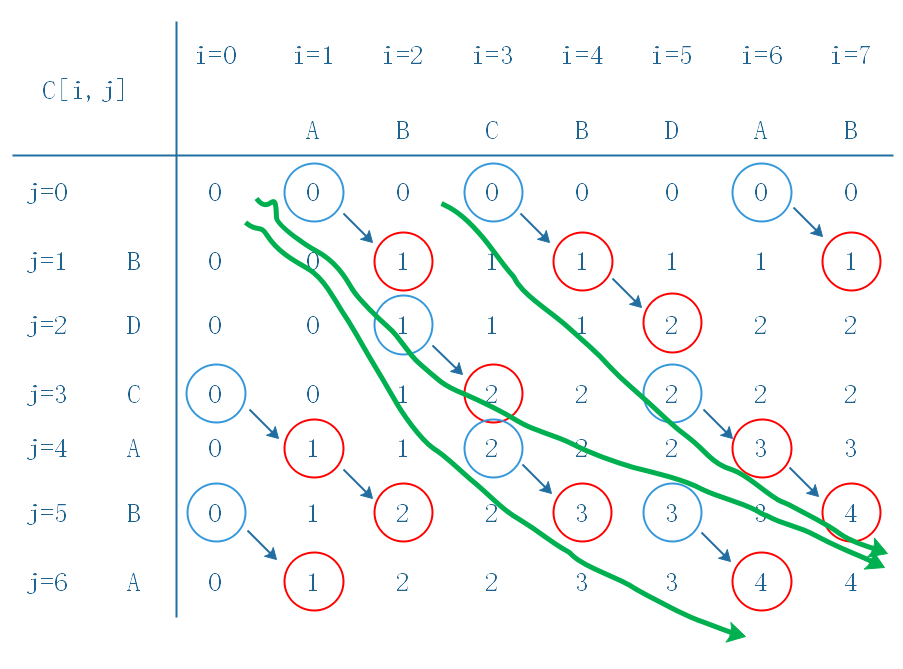
上面算法输出4条最长公共子序列，其中有一个重复，你能找出重复的路径吗？最长公共子序列的三条路径(绿线表示)如下：

---

贪心算法(Greedy Algorithm)

贪心算法的属性

  贪婪(心)算法要求每一次选择时，都选择局部最优的选择，当把这些选择累计起来得到的全局解，也是全局最优解。换句话说，想要使用贪婪算法，问题同样必须具有最优子结构，同动态规划不同的是，我们要用贪心选择来改写一般的动态规划的最优子结构。但并不是所有的最优子结构都可以有贪心选择来改写，如果问题可以改用贪心选择来改写最优子结构，我们称这个问题具有贪心选择属性。

  贪心选择属性：我们可以通过作出局部最优的选择，来构造全局最优解。即贪心选择得到的解与剩余子问题的最优解的组合，就是全局最优解或全局最优解之一。在利用贪心算法求解时，我们需要先证明问题具有贪心选择属性。

  动态规划问题一般是自下向上求解，贪心算法多数是自上向下，在一个大问题上我们进行贪心选择，得到一个贪心选择项加上一个子问题，在对子问题进行贪心选择。当然也有自下向上设计的贪心算法，例如最小生成树中用到的Prim算法。

应用实例：活动选择问题

  假设我们有n个活动