本文详细介绍了决策树算法，包括ID3、C4.5和CART的区别，以及如何处理连续型特征。接着，讨论了决策树剪枝的原因和策略，如预剪枝和后剪枝，并解释了为何剪枝能降低过拟合风险。最后，探讨了决策树模型的参数，如基尼系数、信息熵、最大深度、最小样本划分数等，强调了这些参数在防止过拟合和优化模型中的作用。
决策树算法
ID3：信息增益
C4.5：信息增益率（解决ID3问题，考虑自身熵）
CART：使用GINI系数来当做衡量标准
GINI系数：
Gini(p)=∑k=1Kpk(1−pk)=1−∑k=1Kpk2Gini(p)=\sum^K_{k=1}p_k(1-p_k)=1-\sum^K_{k=1}p_k^2Gini(p)=∑k=1Kpk(1−pk)=1−∑k=1Kpk2
(和熵的衡量标准类似，计算方式不相同)
连续型特征
之前我们讨论的节点或者说特征的划分都是针对离散值，因为离散值可以直接作为分划的节点，当我们的特征是连续型时，我们就需要人为的将其离散化，例如一串连续的数据进行排序，我们可以遍历数据来判断选择一个位置将其分划。
决策树剪枝策略
为什么要剪枝
决策树过拟合风险很大，理论上可以完全分得开数据（构建足够大的数，让每个叶子节点成为一个数据），但是当我们的数据过于庞大时，因为树的分划能力很差，所以数据可能在训练集上表达效果很好，但到了测试集就十分杂乱，表现效果就会很差
剪枝策略
预剪枝
·边建立决策树边进行剪枝的操作（更实用）
·限制深度，叶子节点个数，叶子节点样本数，信息增益量等，当建立的树达到所限制的条件树将不会在继续建立。
后剪枝
·当建立决策树后再来进行剪枝操作
·通过一定的衡量标准
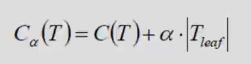
其中:
C(T)表示当前损失 其数值等于叶子节点样本数乘其熵值
TleafT_{leaf}Tleaf指的是叶子节点个数
（叶子节点越多，损失越大）
预剪枝与后剪枝相比，相当于简化了模型，降低了复杂度，可以更省时间
数模型参数
1.criterion gini(基尼系数) or entropy(信息熵)
2.splitter best or random前者是在所有特征中找最好的切分点后者是在部分特征中（数据量大的时候)
3.max_features None（所有），log2，sqrt，N特征小于50的时候一般使用所有的
4.max_depth 数据少或者特征少的时候可以不管这个值，如果模型样本量多，特征也多的情况下，可以尝试限制下
5.min_samples_split如果某节点的样本数少于min_samples_split，则不会继续再尝试选择最优特征来进行划分，如果样本量不大，不需要管这个值。如果样本量数量级非常大，则推荐增大这个值。
6.min_samples_leaf这个值限制了叶子节点最少的样本数，如果某叶子节点数目小于样本数，则会和兄弟节点一起被剪枝，如果样本量不大，不需要管这个值,大些如10万可是尝试下
7.min_weight_fraction_leaf这个值限制了叶子节点所有样本权重和的最小值，如果小于这个值，则会和兄弟节点一起被剪枝默认是0，就是不考虑权重问题。一般来说，如果我们有较多样本有缺失值，或者分类树样本的分布类别偏差很大，就会引入样本权重，这时我们就要注意这个值了。
8.max_leaf_nodes 通过限制最大叶子节点数，可以防止过拟合，默认是"None"，即不限制最大的叶子节点数。如果加了限制，算法会建立在最大叶子节点数内最优的决策树。如果特征不多，可以不考虑这个值，但是如果特征分成多的话，可以加以限制具体的值可以通过交叉验证得到。
9.class_weight 指定样本各类别的的权重，主要是为了防止训练集某些类别的样本过多导致训练的决策树过于偏向这些类别。这里可以自己指定各个样本的权重如果使用"balanced"，则算法会自己计算权重，样本量少的类别所对应的样本权重会高
扫一扫
2627
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
