【Algorithm】Day-5

本篇文章主要讲解算法练习题

---

1  删除链表的倒数第 N 个节点

链接：19. 删除链表的倒数第 N 个结点 - 力扣（LeetCode）

题目描述：

给你一个链表，删除链表的倒数第 n 个结点，并且返回链表的头结点。

示例 1：

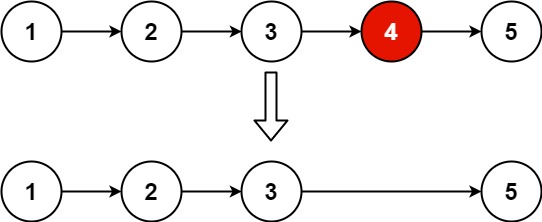
输入：head = [1,2,3,4,5], n = 2
输出：[1,2,3,5]

示例 2：

输入：head = [1], n = 1
输出：[]

示例 3：

输入：head = [1,2], n = 1
输出：[1]

提示：

• 链表中结点的数目为 sz
• 1 <= sz <= 30
• 0 <= Node.val <= 100
• 1 <= n <= sz

题目解析：

        这道题目的题意比较简单，就是题目中会给你一个单链表的头节点，然后给你一个数字 n，题目要求你删除链表中的倒数第 n 个节点，然后最终返回删除该节点之后的链表的头节点。比如：head = [1, 2, 3, 4, 5]，n = 5，删除掉链表中的倒数第 5 个节点，所以返回的链表为 head = [2, 3, 4, 5]。

算法解析：

        由于题目中是单链表，没法通过后向节点找到其前向节点，所以要删除倒数第 n 个节点，首先需要先从头开始找到要删除的节点 del，还需要找到 del 的前一个节点 prev，然后让 prev->next = cur->next，这样就相当于从链表中删去了 cur 节点。所以最容易想的算法就是：利用链表的长度。首先我们利用一个 cur 指针算出链表的长度 len，然后要删除的节点就是从头开始的第 len - n + 1 个节点，然后我们让 del 从头节点开始，向后走 len - n 次，同时用 prev 节点记录其前一个节点，然后让 prev->next = del->next，最后返回 head 就可以了。但是有种特殊情况需要处理一下，那就是删除的节点是头节点的情况，此时 len -  k = 0，那么 del 依然是 head，prev 也是 head，这时候其实没有达到删除头节点的效果，这时候需要特殊处理，可以利用添加哨兵位或者返回 head->next 就可以了：

class Solution 
{
public:
    ListNode* removeNthFromEnd(ListNode* head, int n) 
    {
        //首先计算出连链表的长度
        int len = 0;
        ListNode* cur = head;
        while (cur)
        {
            ++len;
            cur = cur->next;
        }

        //创建哨兵位
        //ListNode* phead = new ListNode(0, head);
        //ListNode* del = head;
        //ListNode* prev = phead;

        //for (int i = 0; i < len - n; ++i)
        //{
        //    prev = del;
        //   del = del->next;
        //}

        //prev->next = del->next;
        //ListNode* ret = phead->next;
        //delete phead;

        //return ret;

        //特殊处理
        if (len == n) return head->next;

        ListNode* del = head;
        ListNode* prev = head;

        for (int i = 0; i < len - n; ++i)
        {
            prev = del;
            del = del->next;
        }

        prev->next = del->next;

        return head;
    }
};

        上面那种算法遍历了两次链表，接下来我们可以优化算法，使其只遍历一遍链表，首先我们创建一个哨兵位 phead，再创建两个指针，left 和 right，left = phead，right = head；我们先让 right 走 n 次，这样 left 和 right 之间就隔了 n 个节点。之后再让left = left->next, right = right->next，直到 right 走到空，这样 left 正好走到了第倒数 n + 1 个节点，此时再让 left->next = left->next->next 就可以了。

代码：

class Solution 
{
public:
    ListNode* removeNthFromEnd(ListNode* head, int n) 
    {
        //先创建一个哨兵位
        ListNode* phead = new ListNode(0, head);

        ListNode* left = phead, *right = head;
        //先让 right 走 n 个节点
        for (int i = 0; i < n; i++) right = right->next;

        //然后让 right 走到空，left 同时向后走
        while (right)
        {
            left = left->next;
            right = right->next;
        }

        //此时 left 位于要删除节点的前一个节点
        left->next = left->next->next;
        ListNode* ret = phead->next;
        delete phead;

        return ret;
    }
};

---

2  判断子序列

链接：392. 判断子序列 - 力扣（LeetCode）

题目描述：

给定字符串 s 和 t ，判断 s 是否为 t 的子序列。

字符串的一个子序列是原始字符串删除一些（也可以不删除）字符而不改变剩余字符相对位置形成的新字符串。（例如，"ace"是"abcde"的一个子序列，而"aec"不是）。

进阶：

如果有大量输入的 S，称作 S1, S2, ... , Sk 其中 k >= 10亿，你需要依次检查它们是否为 T 的子序列。在这种情况下，你会怎样改变代码？

示例 1：

输入：s = "abc", t = "ahbgdc"
输出：true

示例 2：

输入：s = "axc", t = "ahbgdc"
输出：false

提示：

• 0 <= s.length <= 100
• 0 <= t.length <= 10^4
• 两个字符串都只由小写字符组成。

题目解析：

        这道题目就是会给你两个字符串 s 和 t，要去让你判断出 s 是否是 t 的子序列，如果是就返回 true，不是返回 false。其中子序列是原始字符串中删除一些字符之后的字符串，但是原来的相对位置不能改变（原字符串也是子序列），比如："abc" 就是 "canbndc" 的子序列。

算法讲解：

        这道题目还是比较简单的，我们首先利用一个 left 指针和一个 right 指针，left 用来遍历 s 字符串，right 用来遍历 t 字符串，如果 t[right] == s[left]，那就 ++left；当 right 遍历完 t 字符串之后，如果 left 也正好遍历完 s 字符串，那就说明 s 是 t 的子序列，否则就不是 t 的子序列。

代码：

class Solution 
{
public:
    bool isSubsequence(string s, string t) 
    {
        int left = 0, right = 0;//left 来遍历 s, right 来遍历 t
        while (right < t.size())
        {
            if (t[right] == s[left]) ++left;
            if (left == s.size()) break;
            ++right;
        }

        return left == s.size();
    }
};

---

3  存在重复元素 ||

题目描述：

给你一个整数数组 nums 和一个整数 k ，判断数组中是否存在两个 不同的索引 i 和 j ，满足 nums[i] == nums[j] 且 abs(i - j) <= k 。如果存在，返回 true ；否则，返回 false 。

示例 1：

输入：nums = [1,2,3,1], k = 3
输出：true

示例 2：

输入：nums = [1,0,1,1], k = 1
输出：true

示例 3：

输入：nums = [1,2,3,1,2,3], k = 2
输出：false

提示：

• 1 <= nums.length <= 105
• -109 <= nums[i] <= 109
• 0 <= k <= 105

题目解析：

        这道题目会给你一个整数数组 nums 和一个整数 k，题目的要求是在 abs(i - j) <= k 的前提下，如果能找到两个不同的索引 i 和 j， 满足 nums[i] == nums[j]，那就返回 true，否则返回 false。

算法解析：

        这道题目的解法我们可以采用哈希表 + 滑动窗口来实现：

（1） 定义 left = 0, right = 0, unordered_map<int, int> um

（2） 进窗口：um[nums[right]]++，++right

（3） 判断：如果 right - left > k，那就出窗口： um[nums[left]]--，++left

（4） 更细结果：如果 um[nums[right]] > 1，那就返回 true

代码：

class Solution 
{
public:
    bool containsNearbyDuplicate(vector<int>& nums, int k) 
    {
        int left = 0, right = 0;
        unordered_map<int, int> um;
        while (right < nums.size())
        {
            //进窗口
            um[nums[right]]++;

            //判断
            if (right - left > k)
            {
                um[nums[left]]--;
                ++left;
            }

            //更新结果
            if (um[nums[right]] > 1) return true;

            ++right;
        }

        return false;
    }
};