慕课网liuyubobobo老师课程学习笔记---part12：红黑树

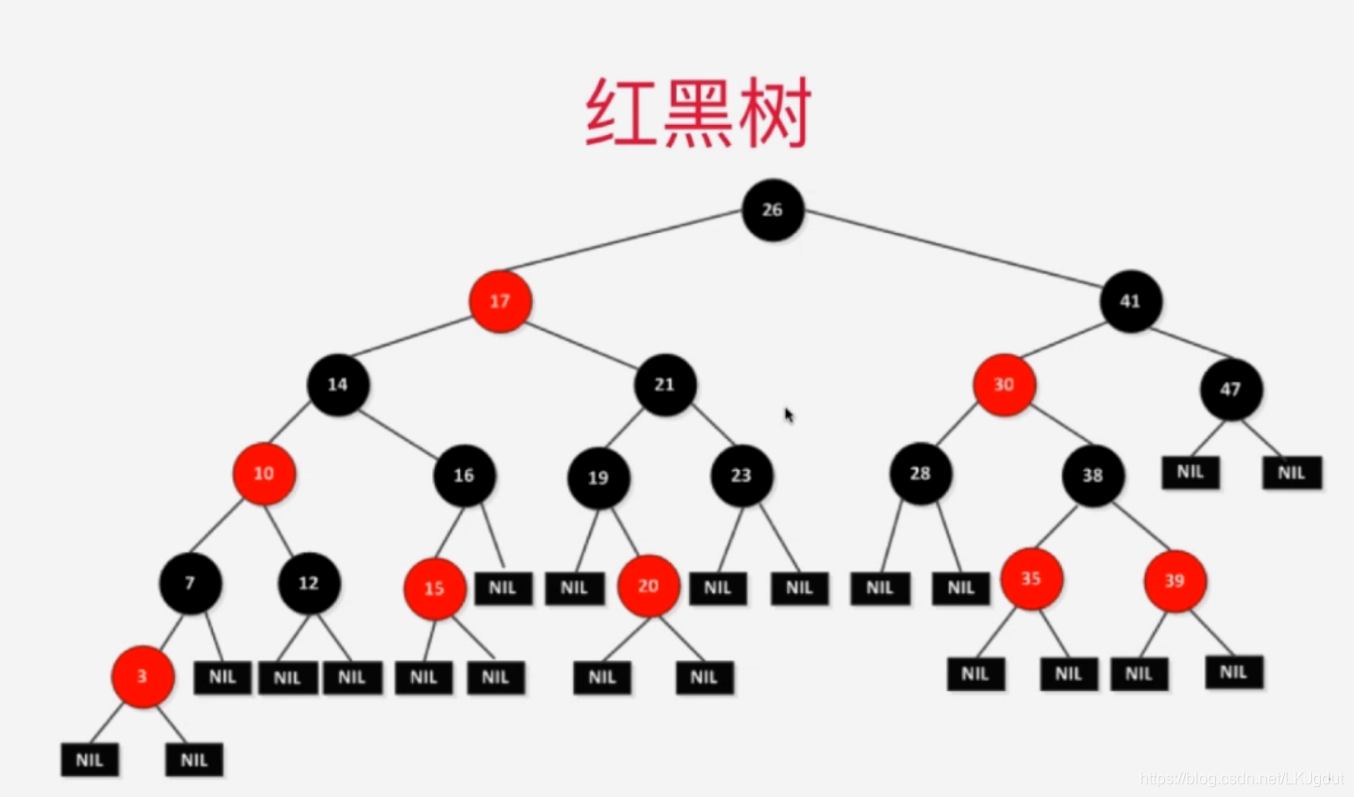
1、红黑树与2-3树

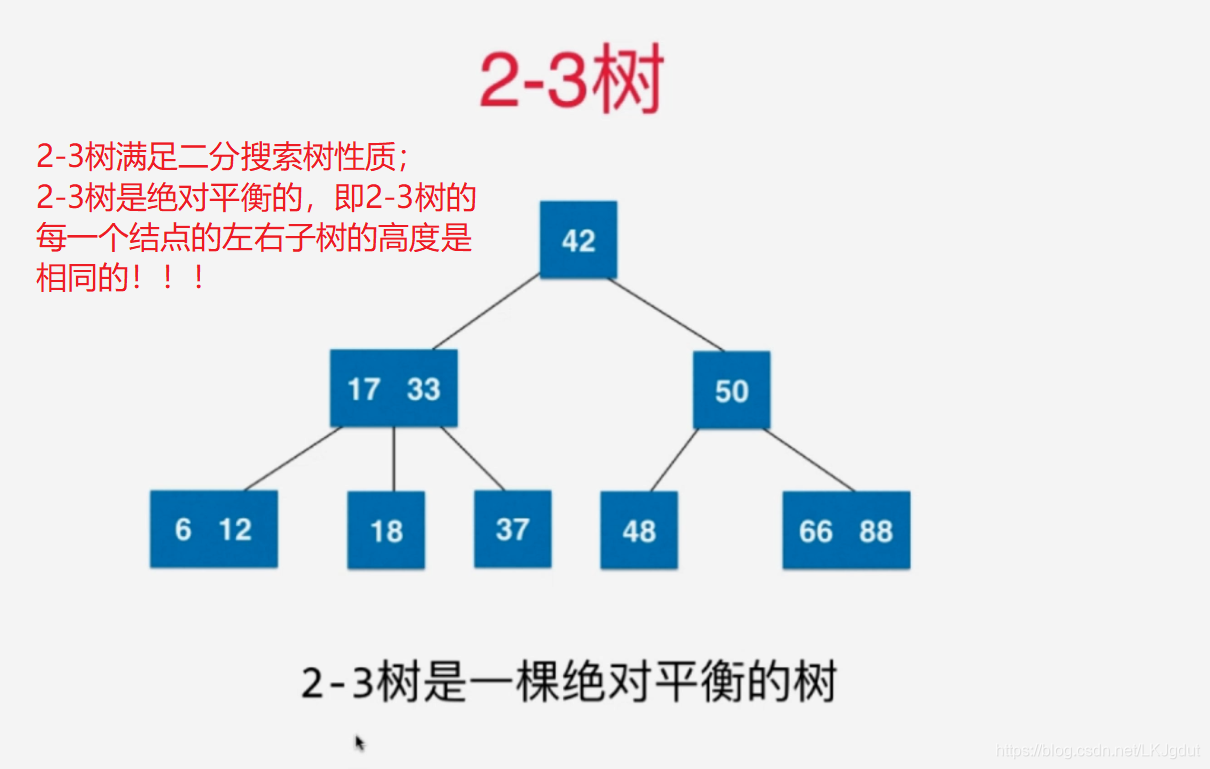
2、树的绝对平衡性

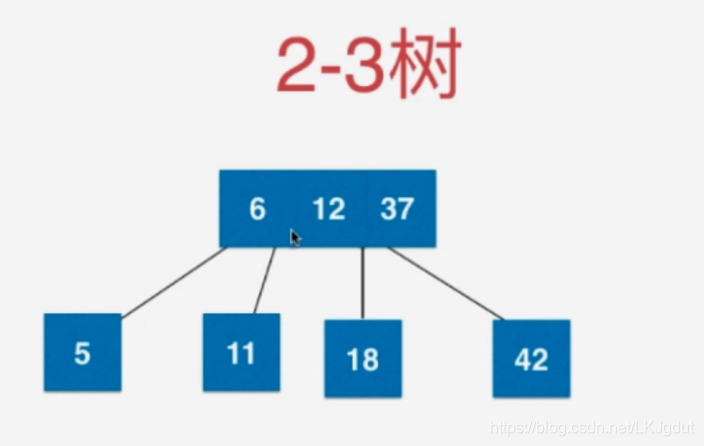
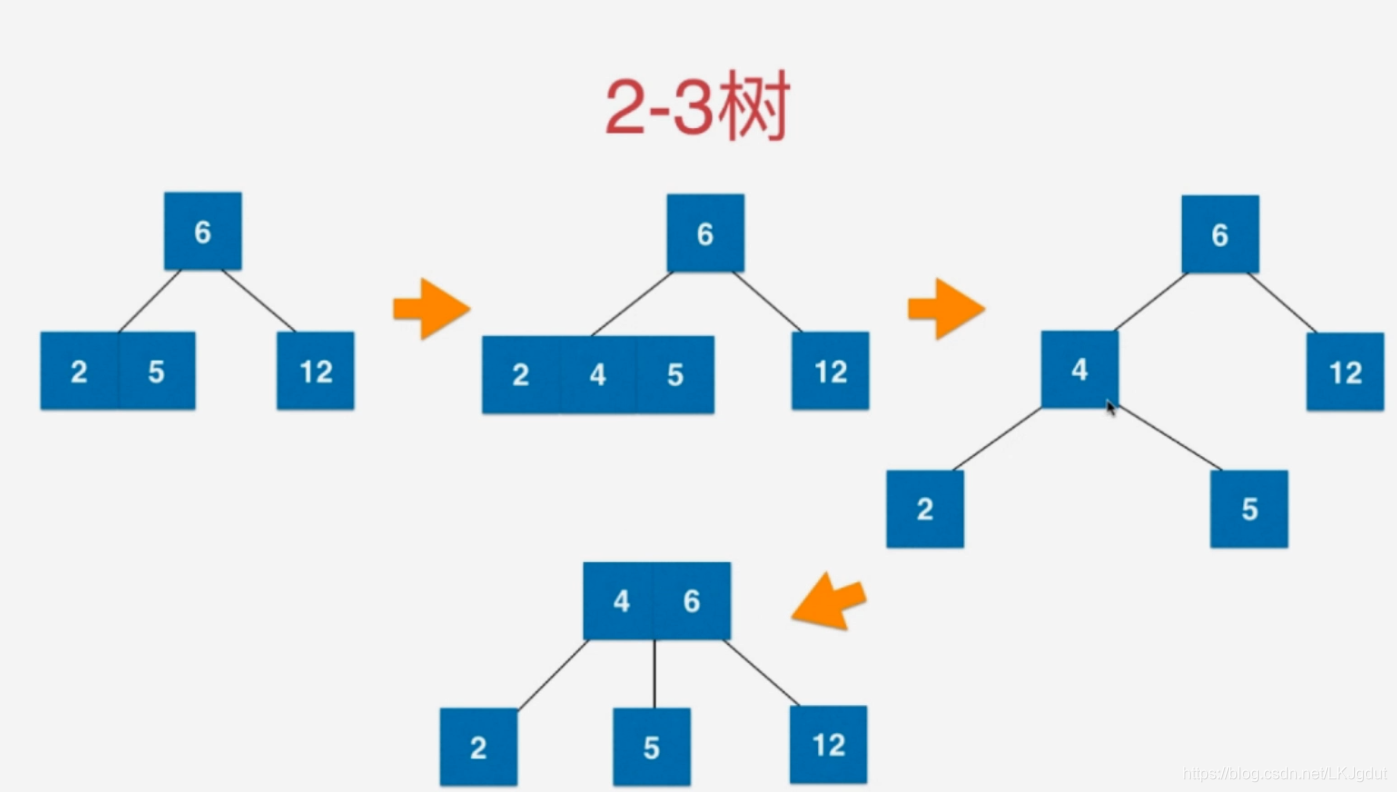
  2-3树在添加结点的时候，新的结点永远不会添加到空的位置，而只会我们最后找到的叶子结点做融合。
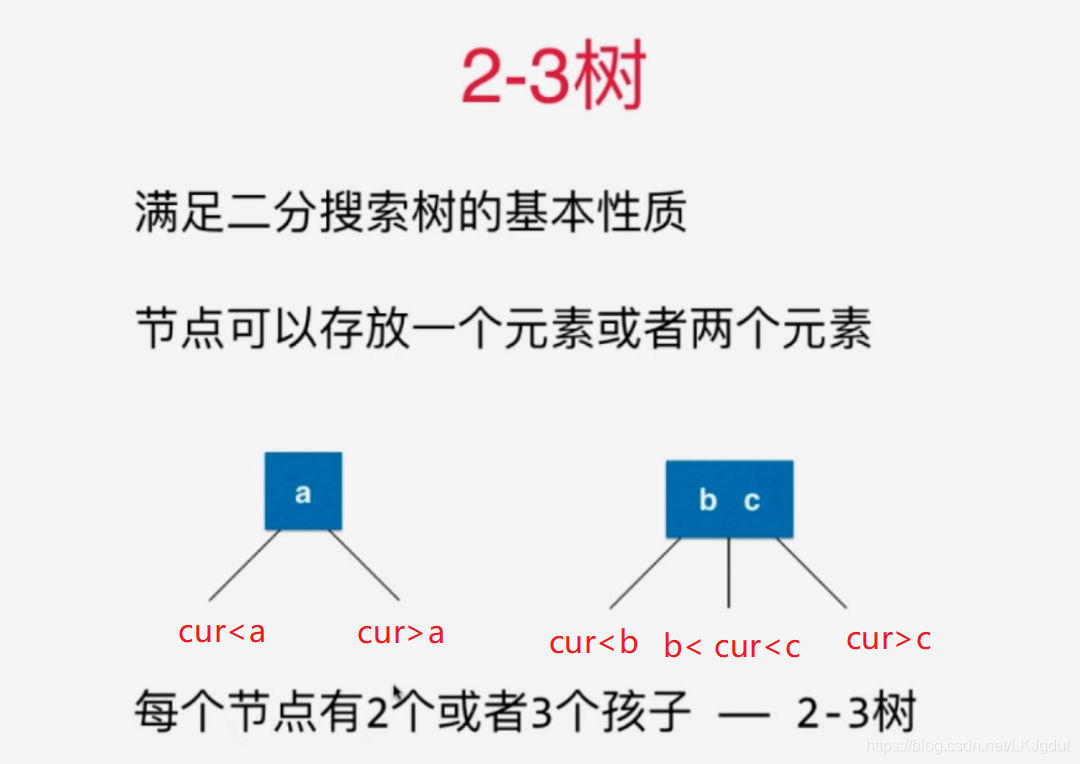
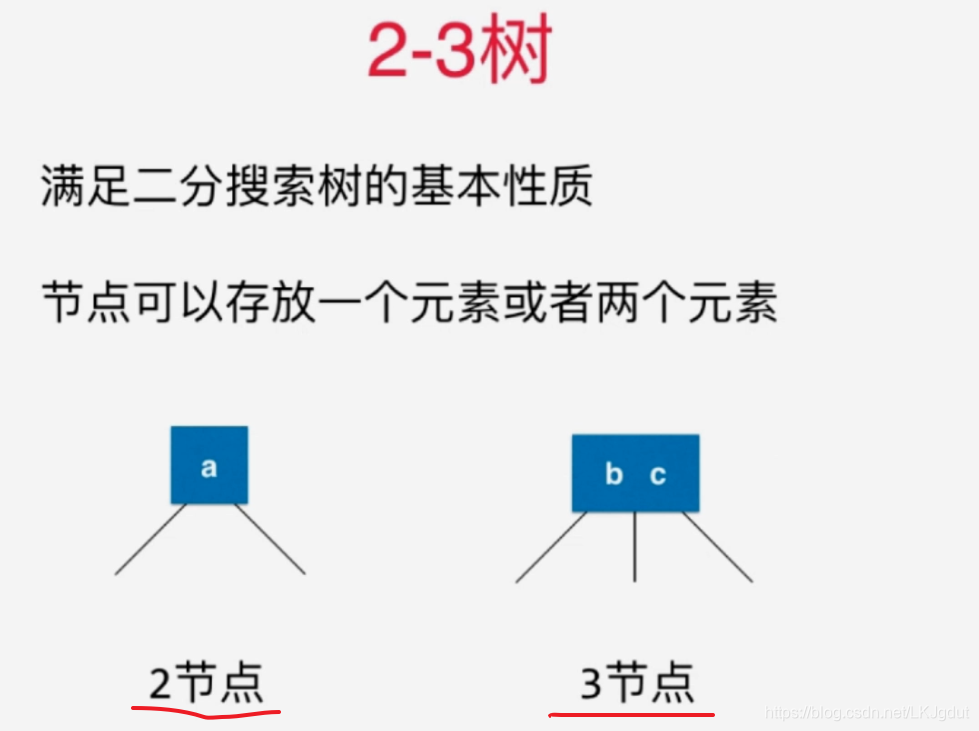
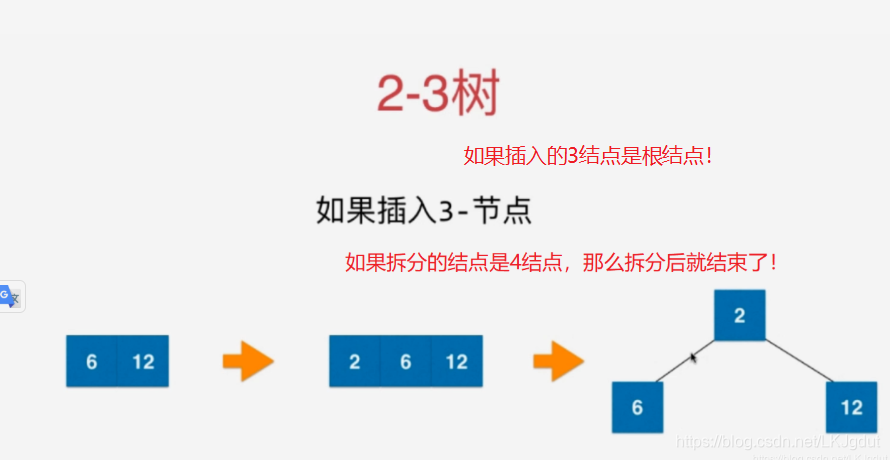
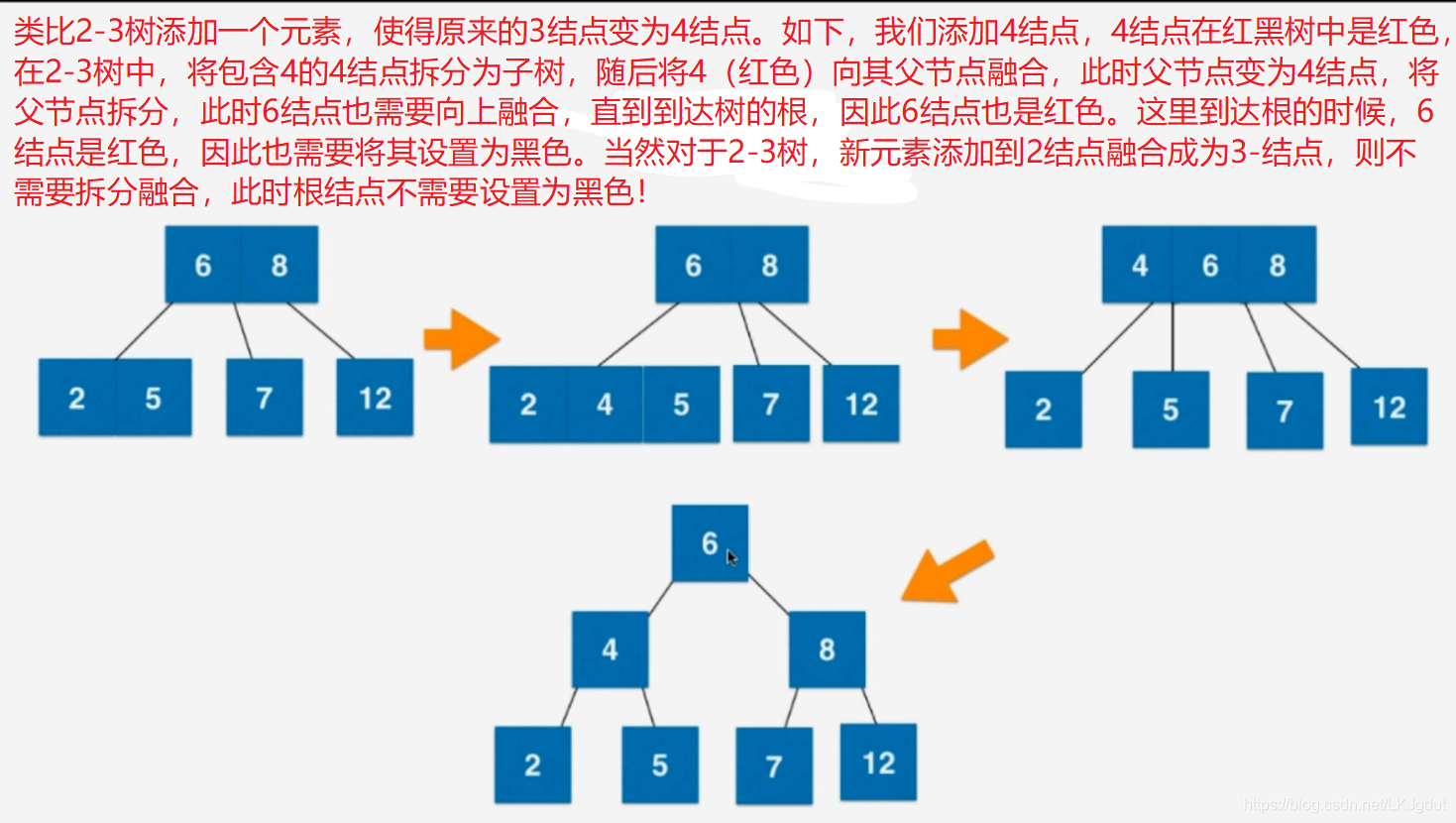
1）对于根结点是4结点的时候（4结点一个结点内有3个元素，2-3树每个结点只能有1或2个元素），我们可以直接将4结点分为一颗子树（由3个2结点组成的树，即每个结点只有一个元素）。
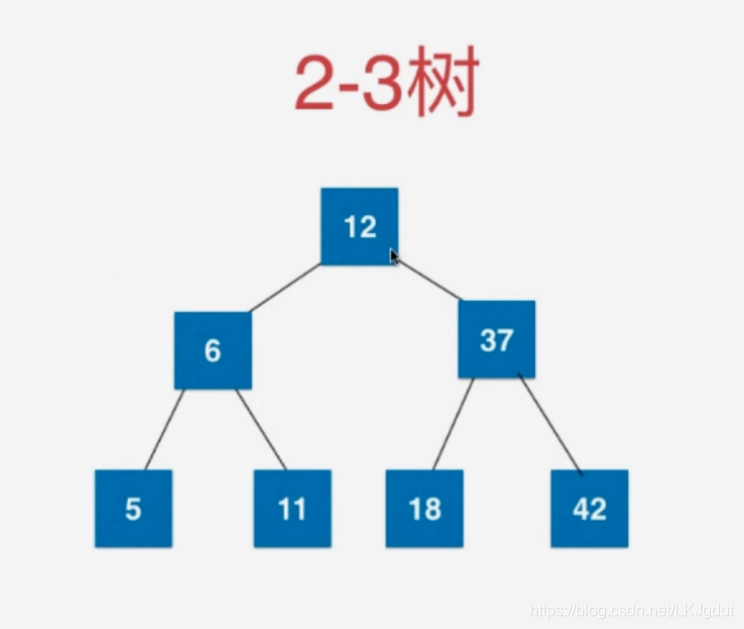
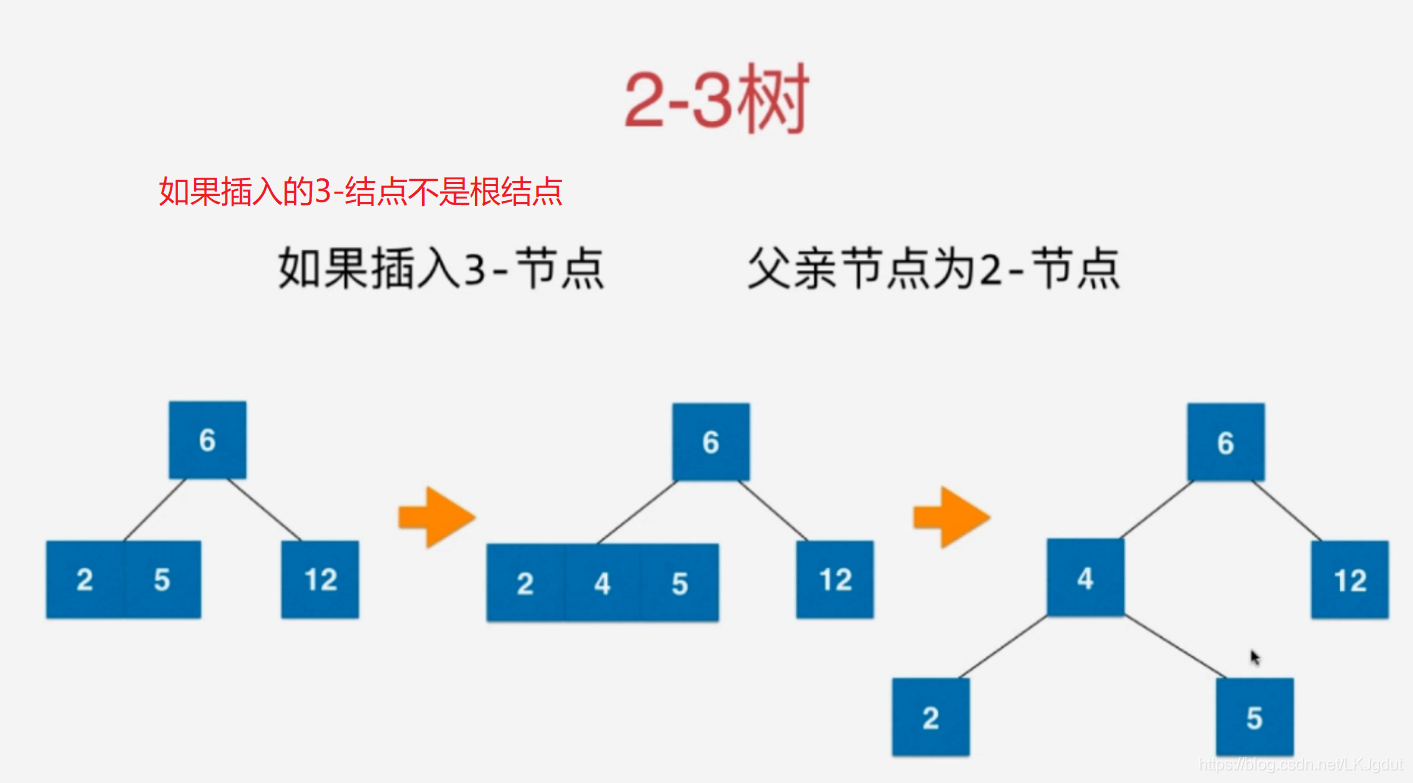
2）对于叶子结点来说，如果该叶子结点因为添加一个元素，从3结点变成4结点，我们先将该结点拆分为由3个2结点组成的树，再将这颗树的根结点与其父节点融合成为一个3结点（如果父结点原来只有一个元素）。这样才能保证2-3树的绝对平衡性！
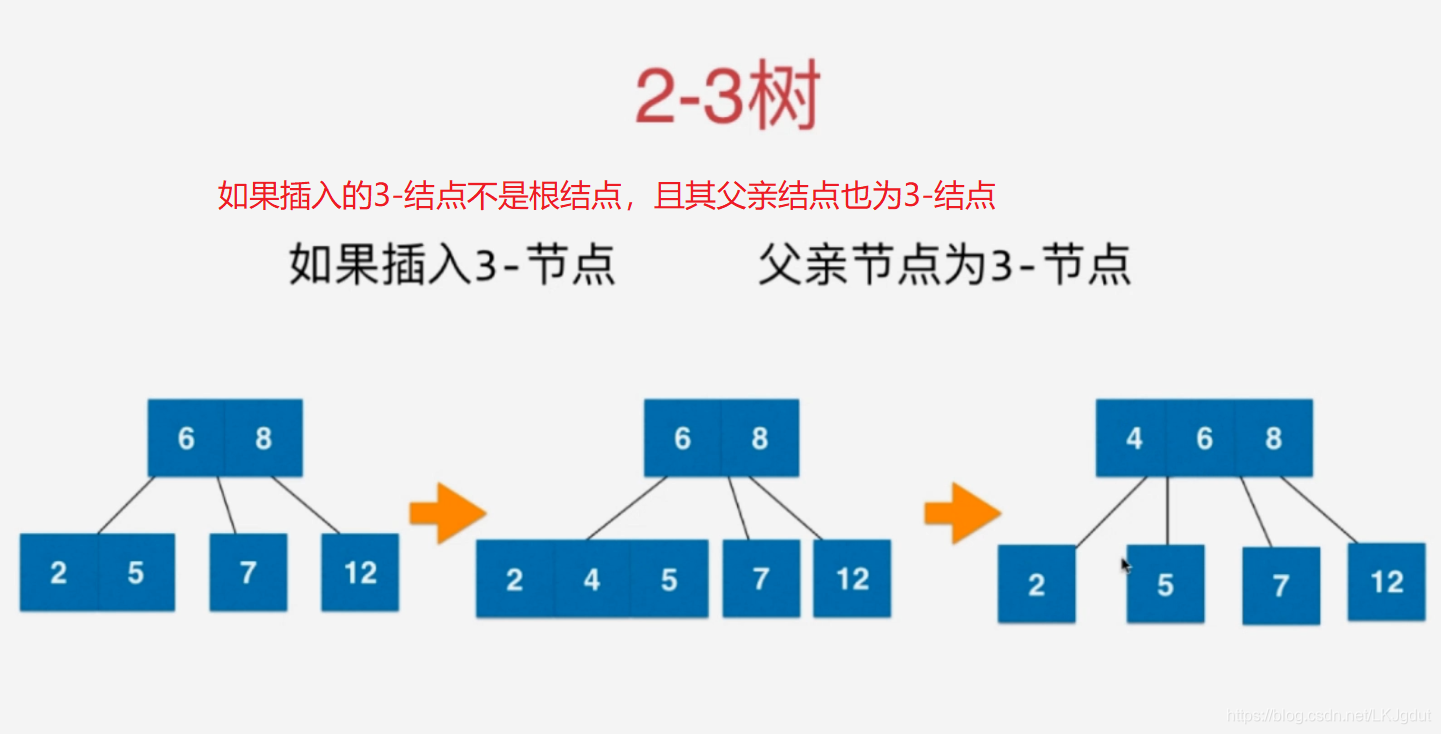
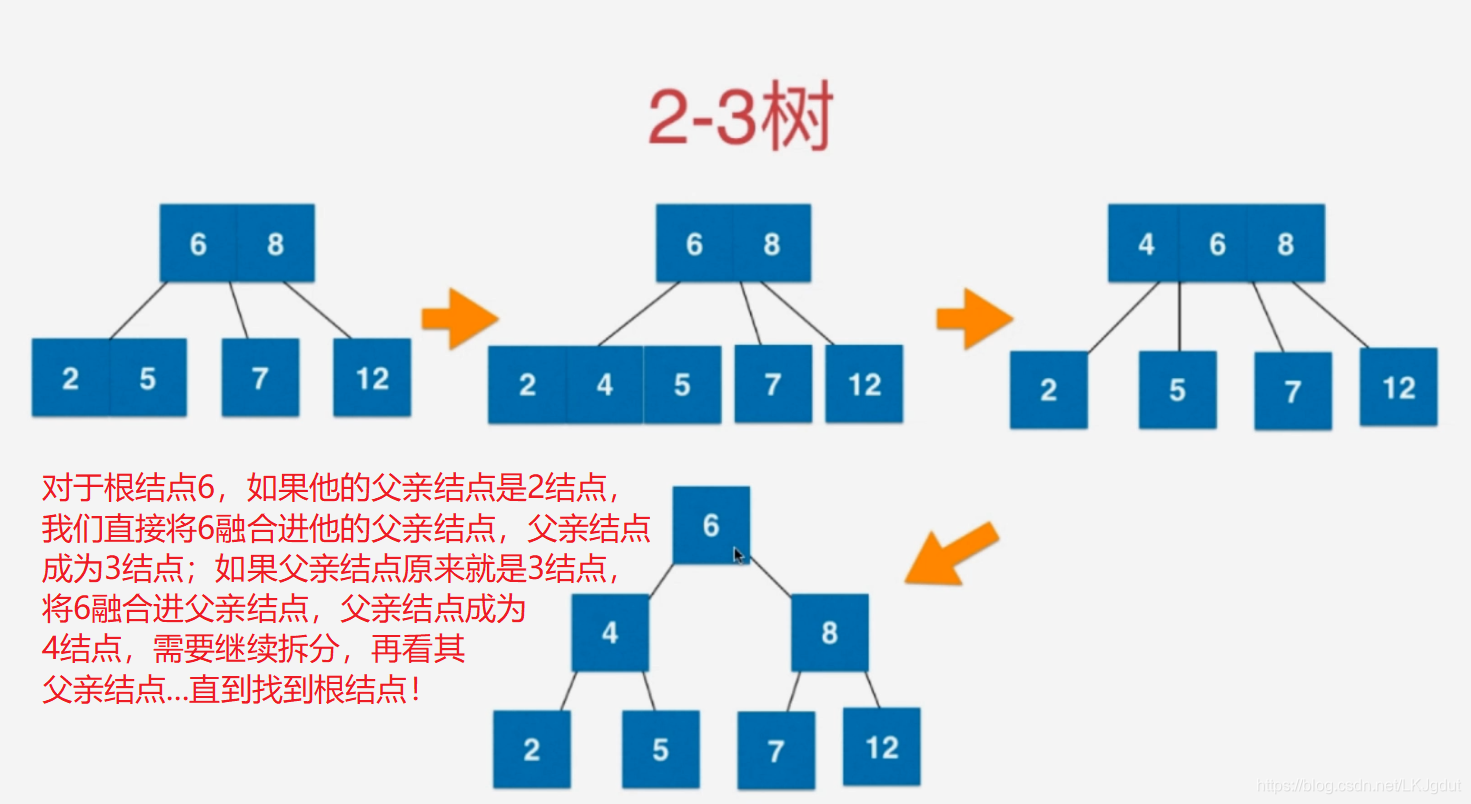
3）在2）中，如果拆分的树的根结点的父结点原来有2个元素，根结点同样融合到父亲结点后，父亲结点成为一个4结点，我们将这个4结点进行分裂，如下：


  2-3树插入的规律如下：

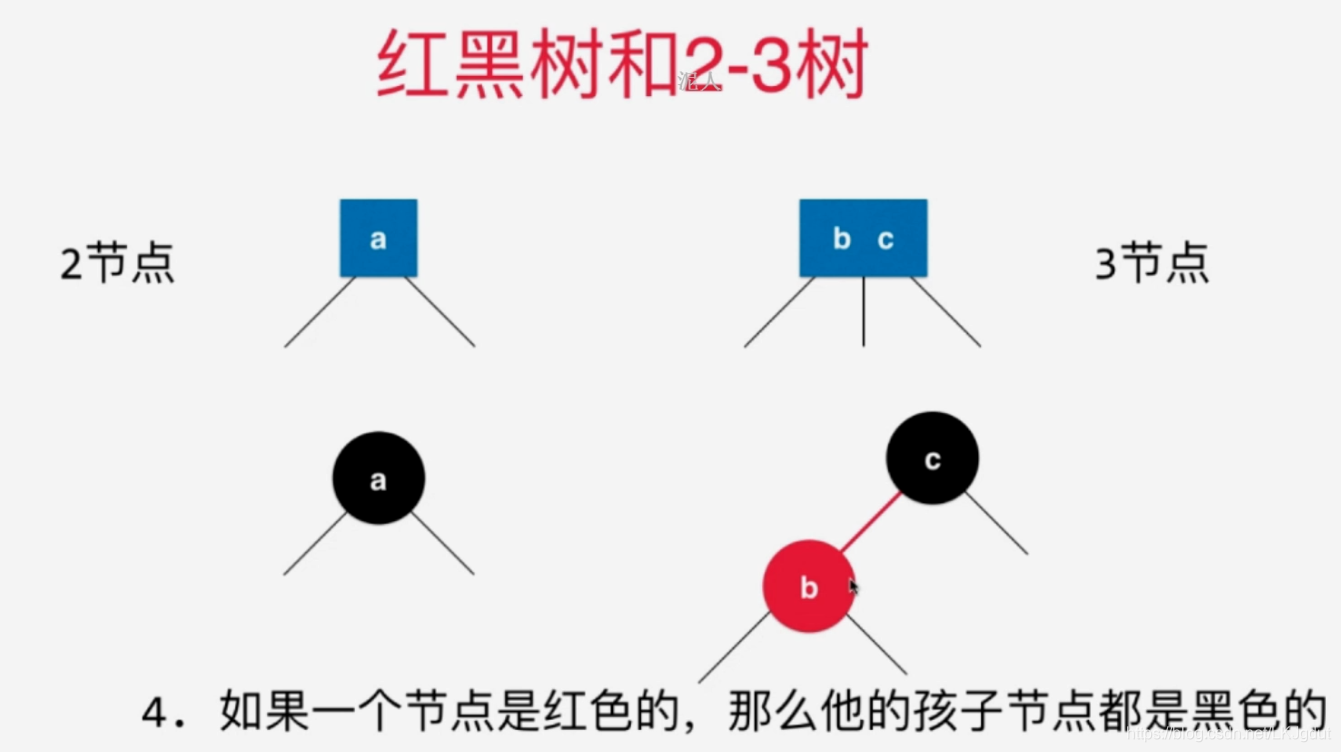
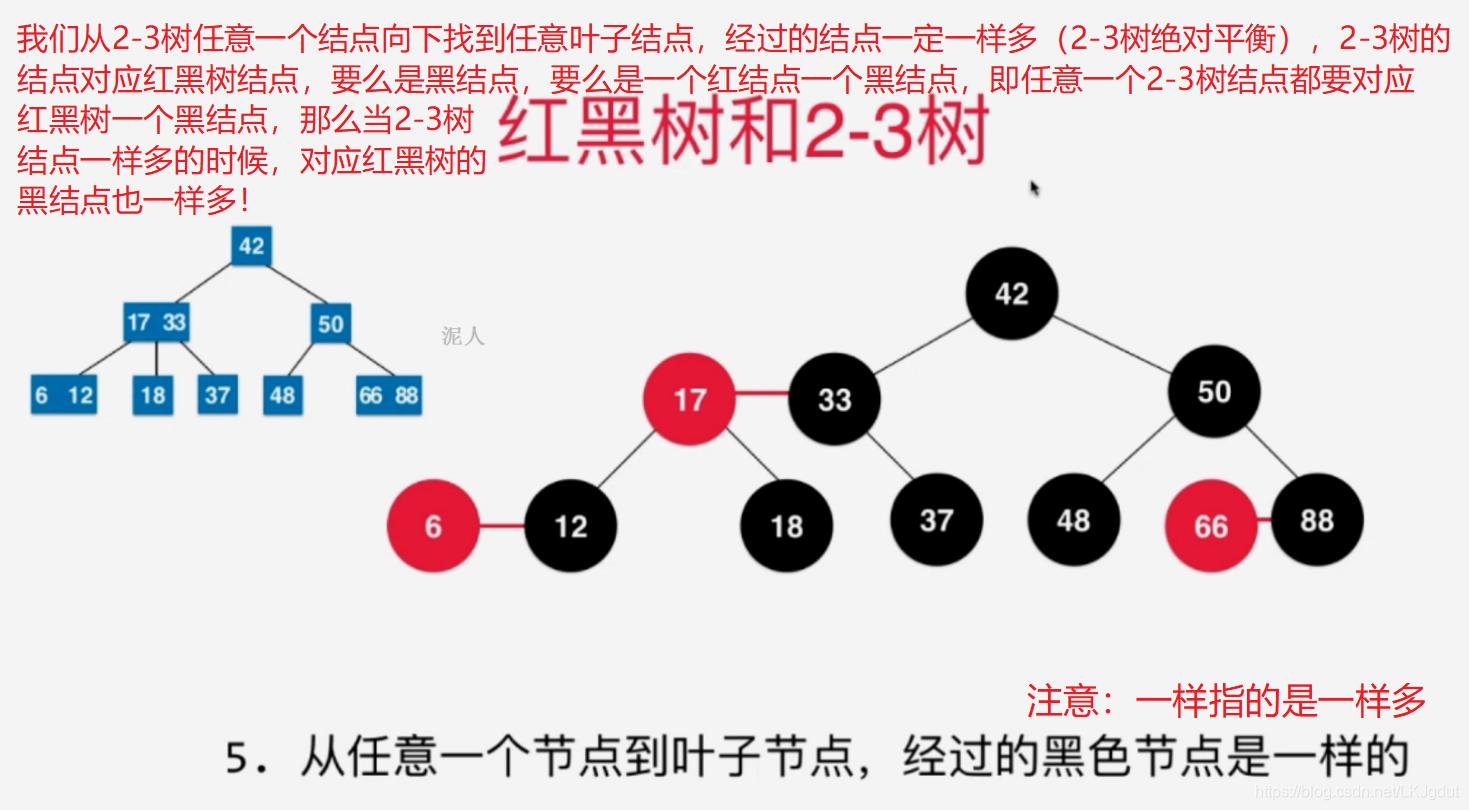
3、红黑树与2-3树的等价性

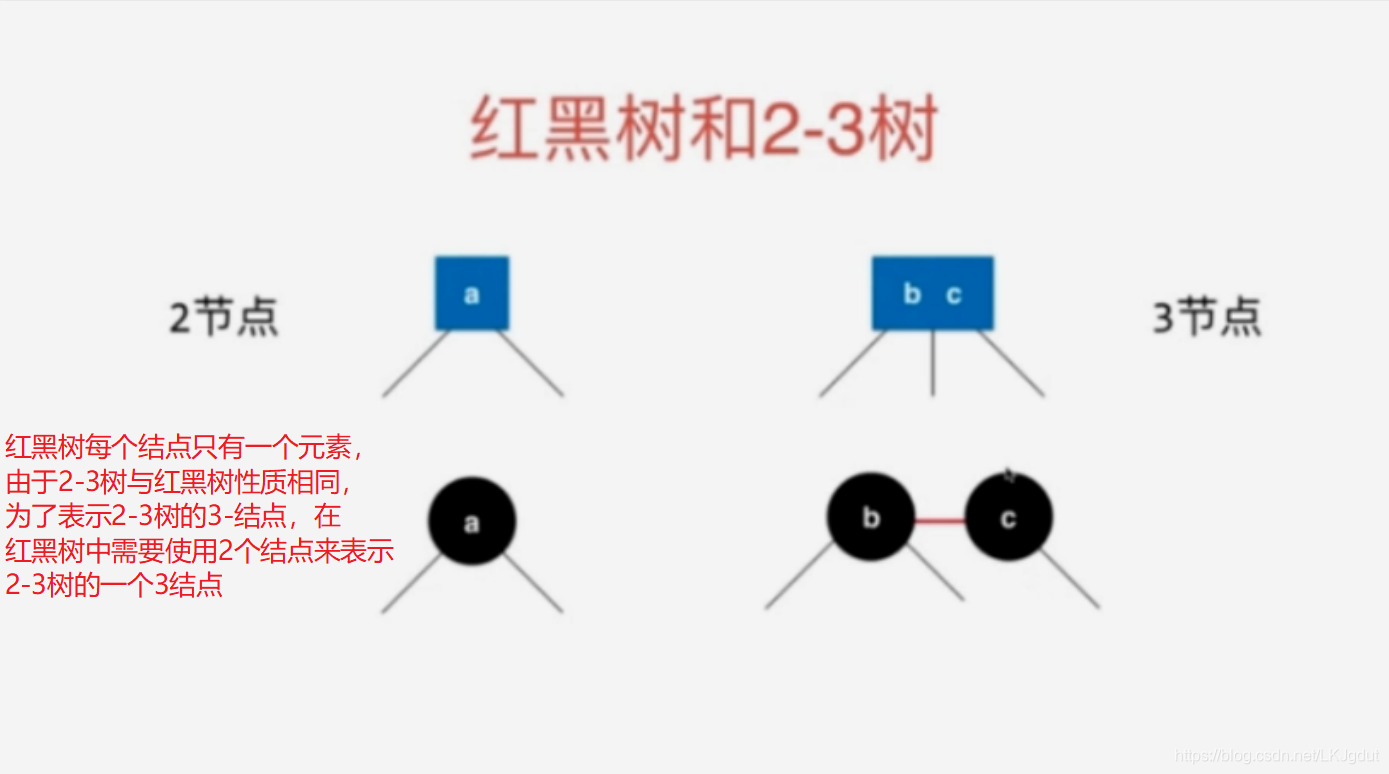
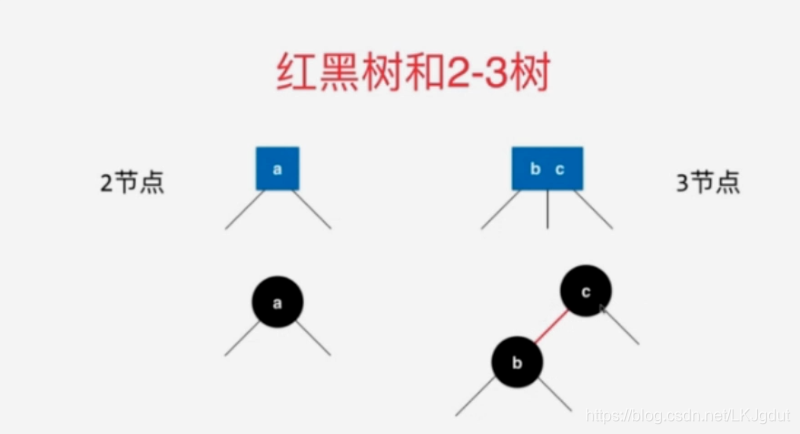
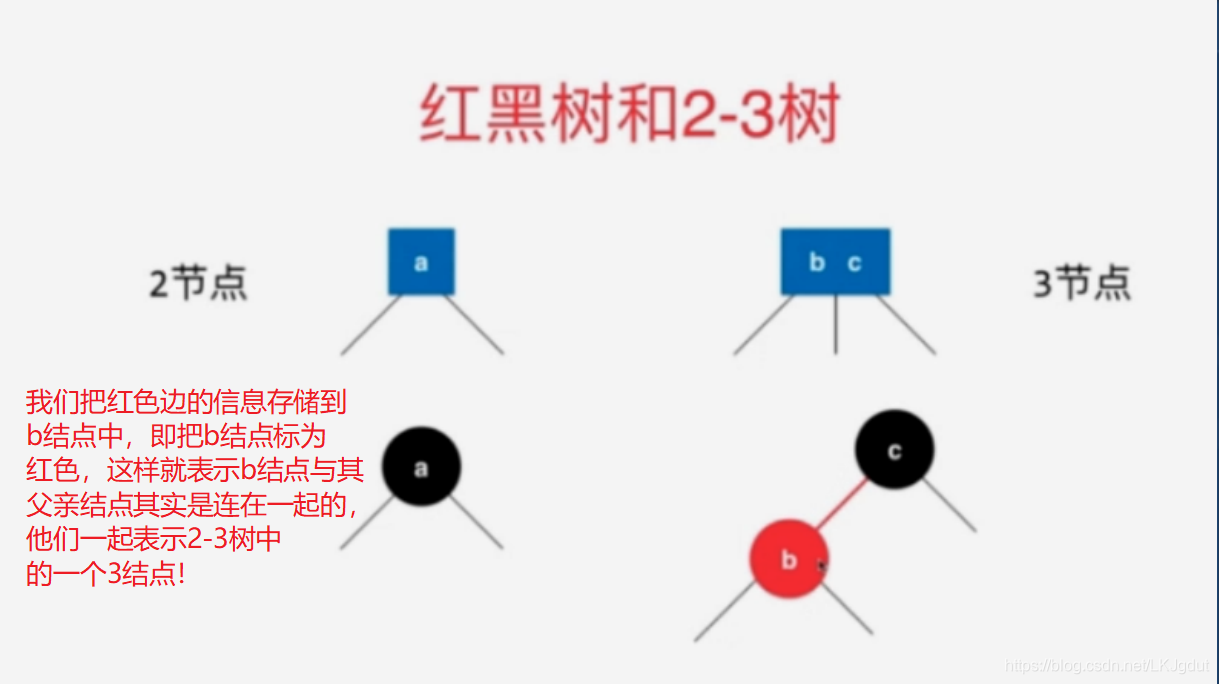
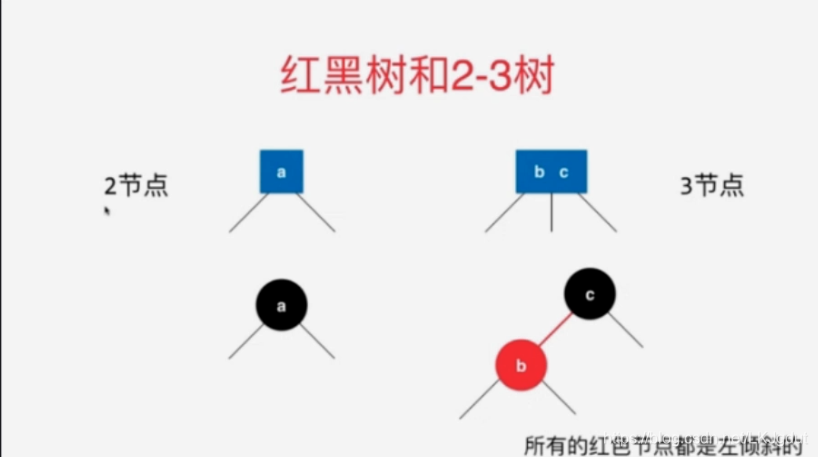
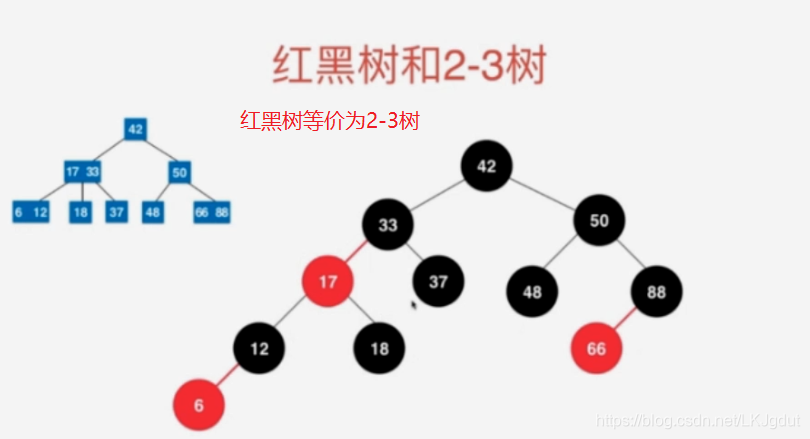
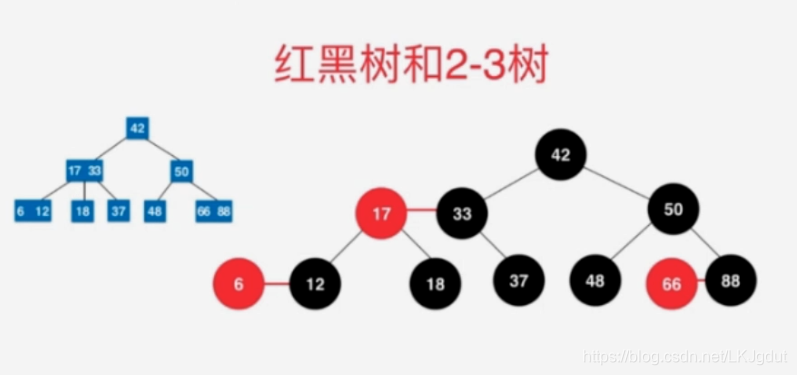
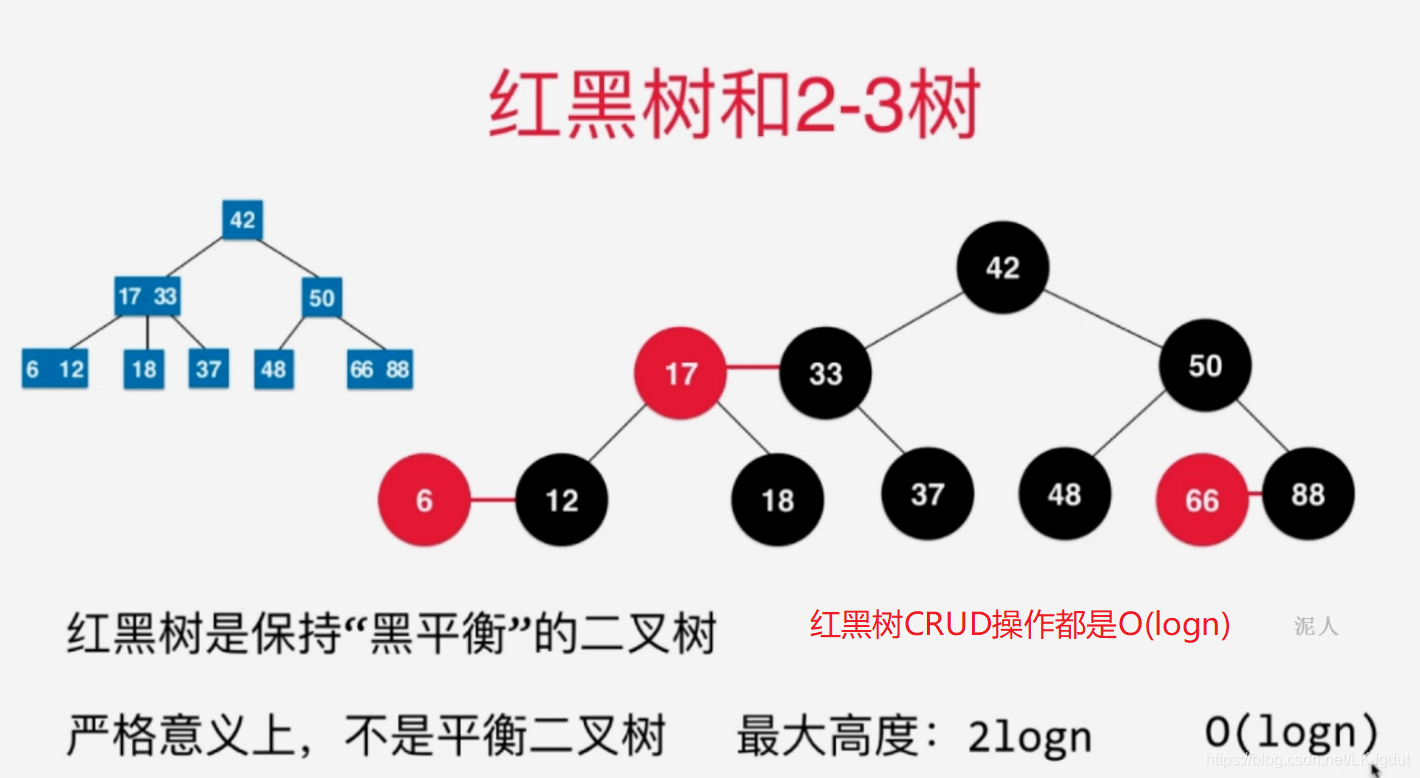
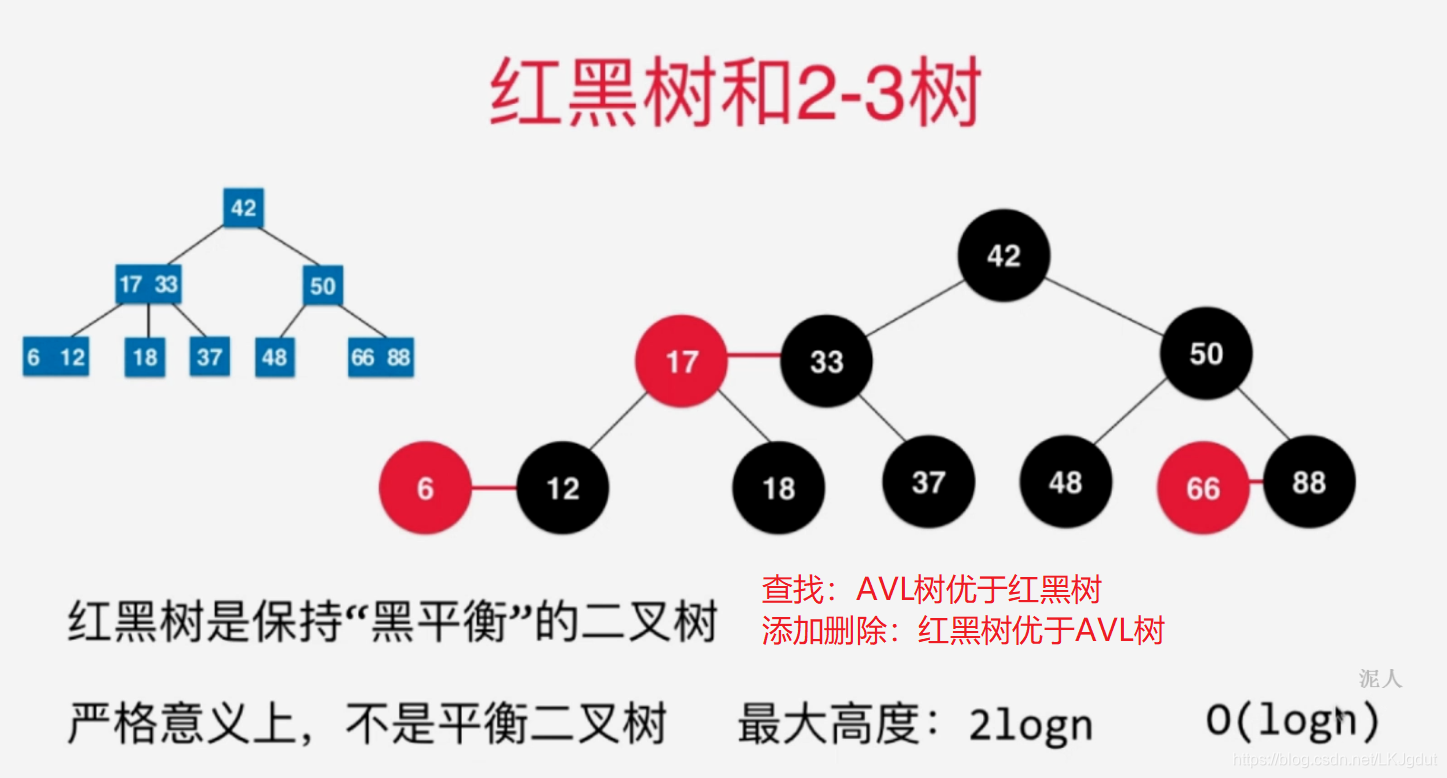
4、红黑树的基本性质与复杂度分析

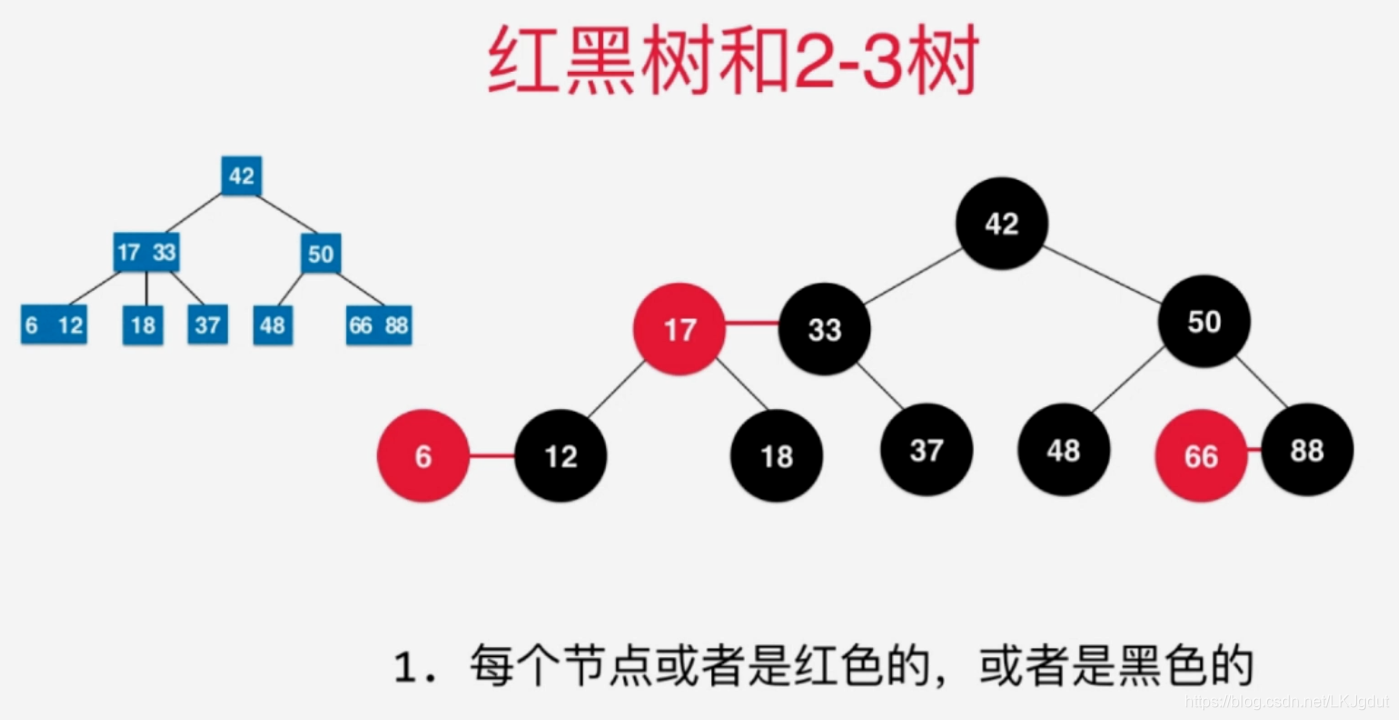
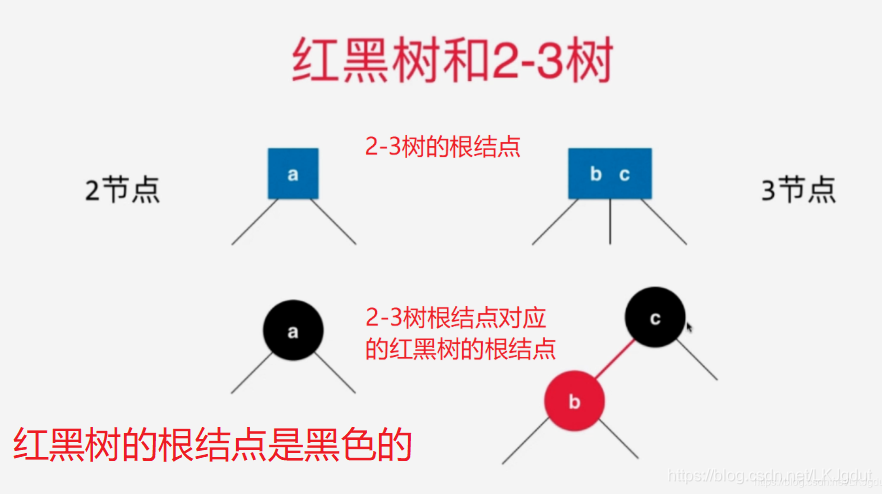
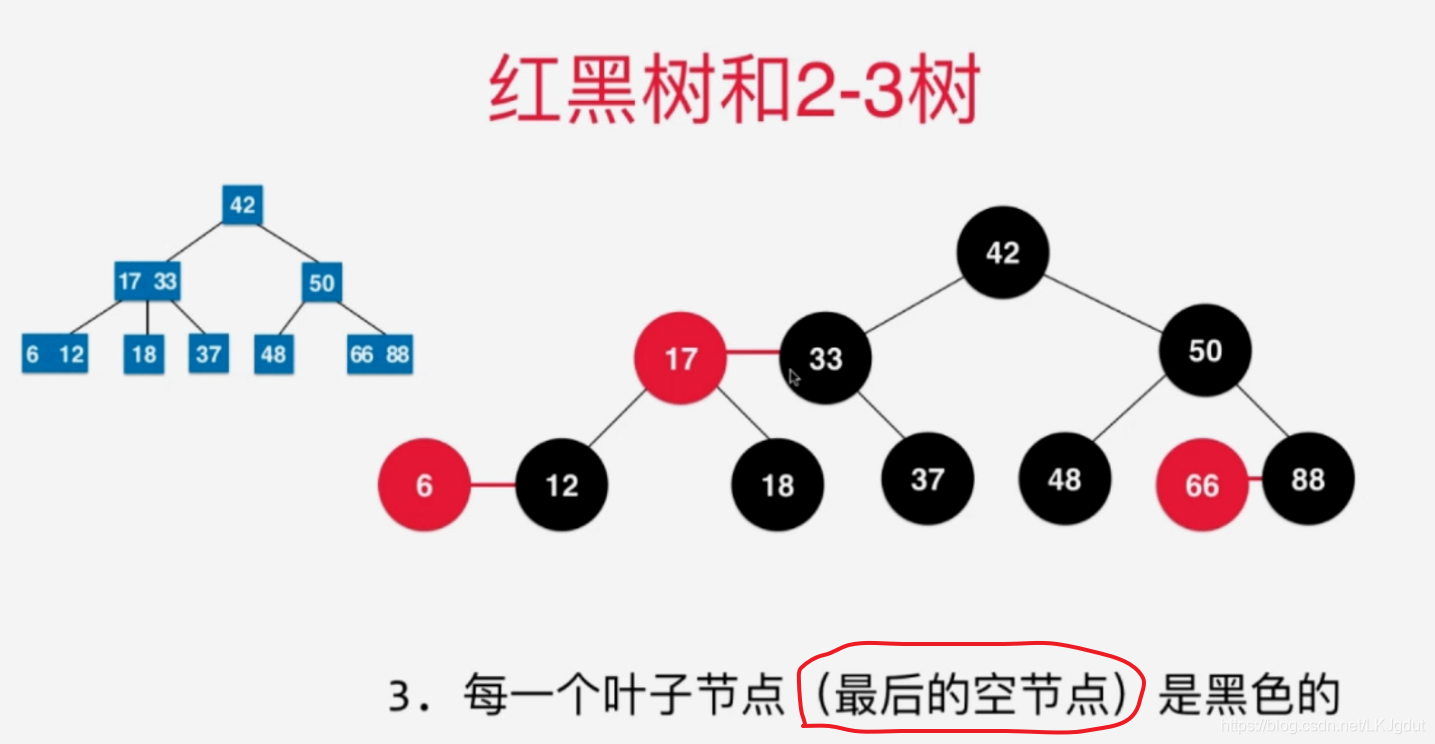
5、保持根结点为黑色和左旋转 + 颜色翻转和右旋转

  红黑树添加结点的规则：
1）在添加红黑树的根结点的时候，我们首先添加红色结点，因为红黑树的根结点必须是黑色，我们需要将根结点变为红色；（对应2-3树中添加一个根结点）
2）需要将根结点变为黑色，这种情况在添加结点的时候（不止是添加根结点）是普遍存在的！

3）添加的新结点（非根结点）在红黑树中**（左子树为空，右子树可以为空或者黑色结点）的黑色结点的左侧**，直接添加即可，表示2-3树的3结点。（对应2-3树中将元素添加到一个2结点，使得2结点变为3结点）。注意，此处黑色结点也可以是红色的，对应2个偏向左侧的红色结点，其实就是对应下面（6）的情况，我们再按下面（6的情u况处理即可！）

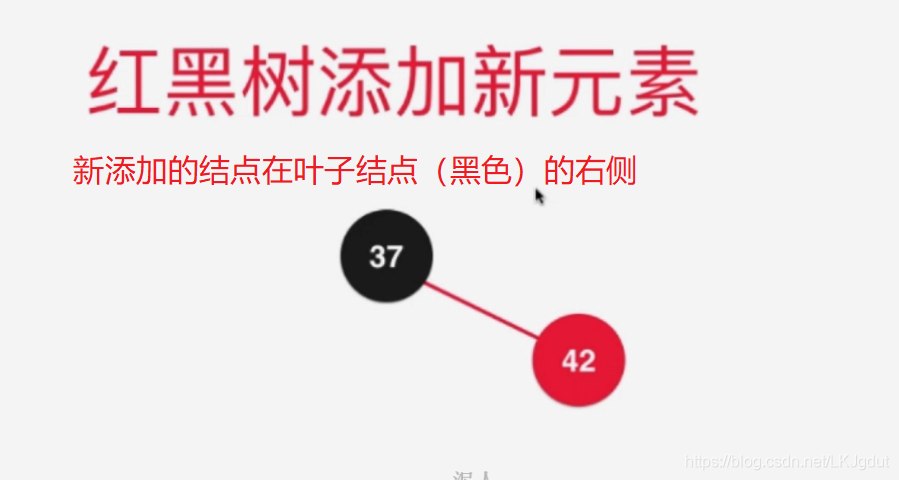
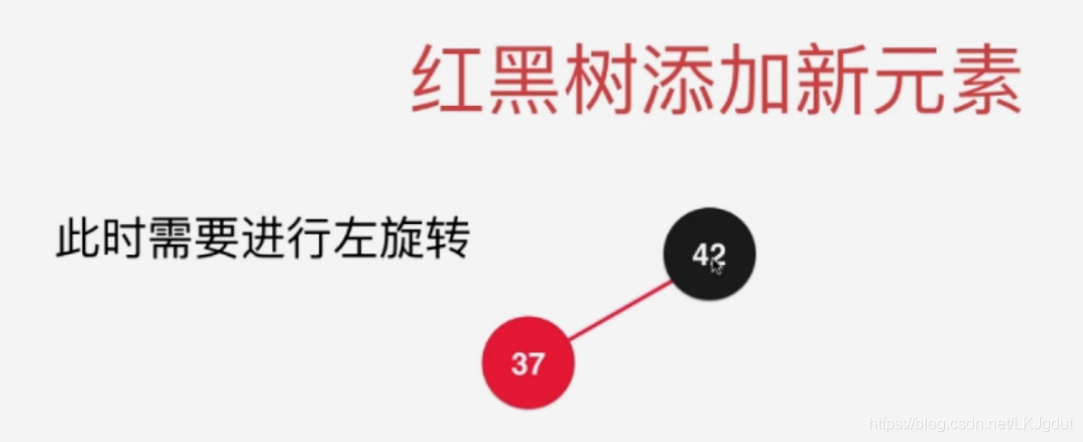
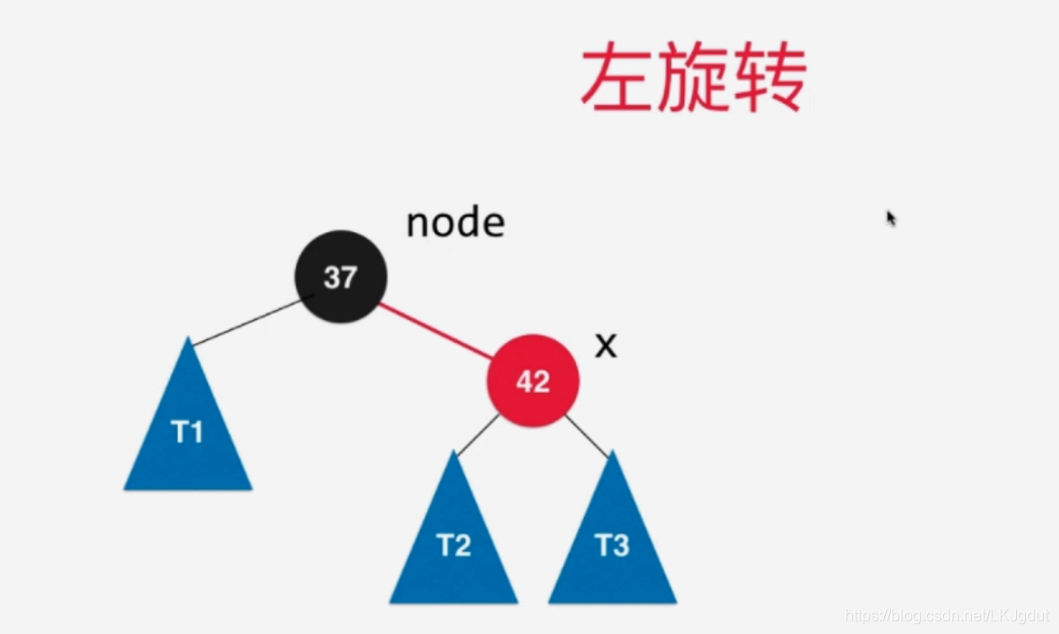
4）添加的新结点（非根结点）在红黑树中**（右子树为空，左子树为空或者黑色结点）的黑色结点的右侧**，此时不满足红黑树的性质（红黑树中所有的红色结点都在左侧），此时需要进行左旋转。（对应2-3树中将元素添加到一个2结点，使得2结点变为3结点）。注意，此处黑色结点也可以是红色的，左旋转后对应2个偏向左侧的红色结点，其实就是对应下面（6）的情况，我们再按下面（6的情况处理即可！）。








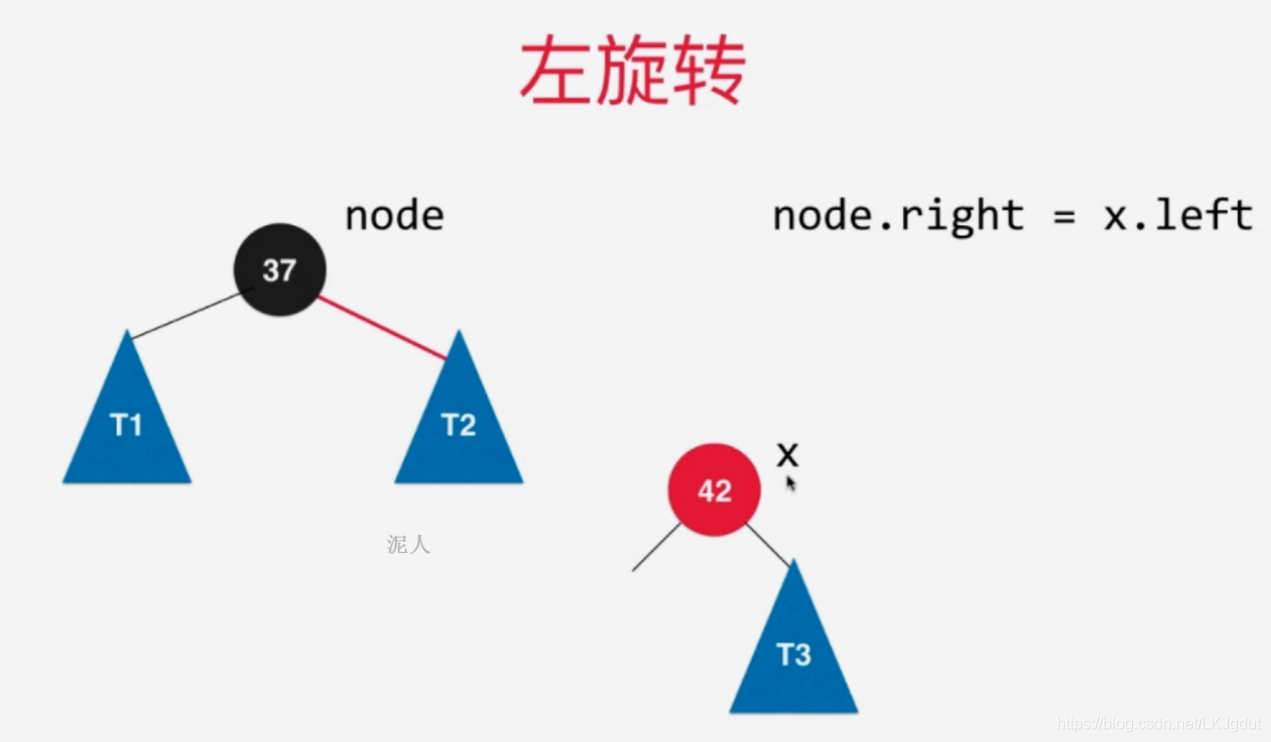
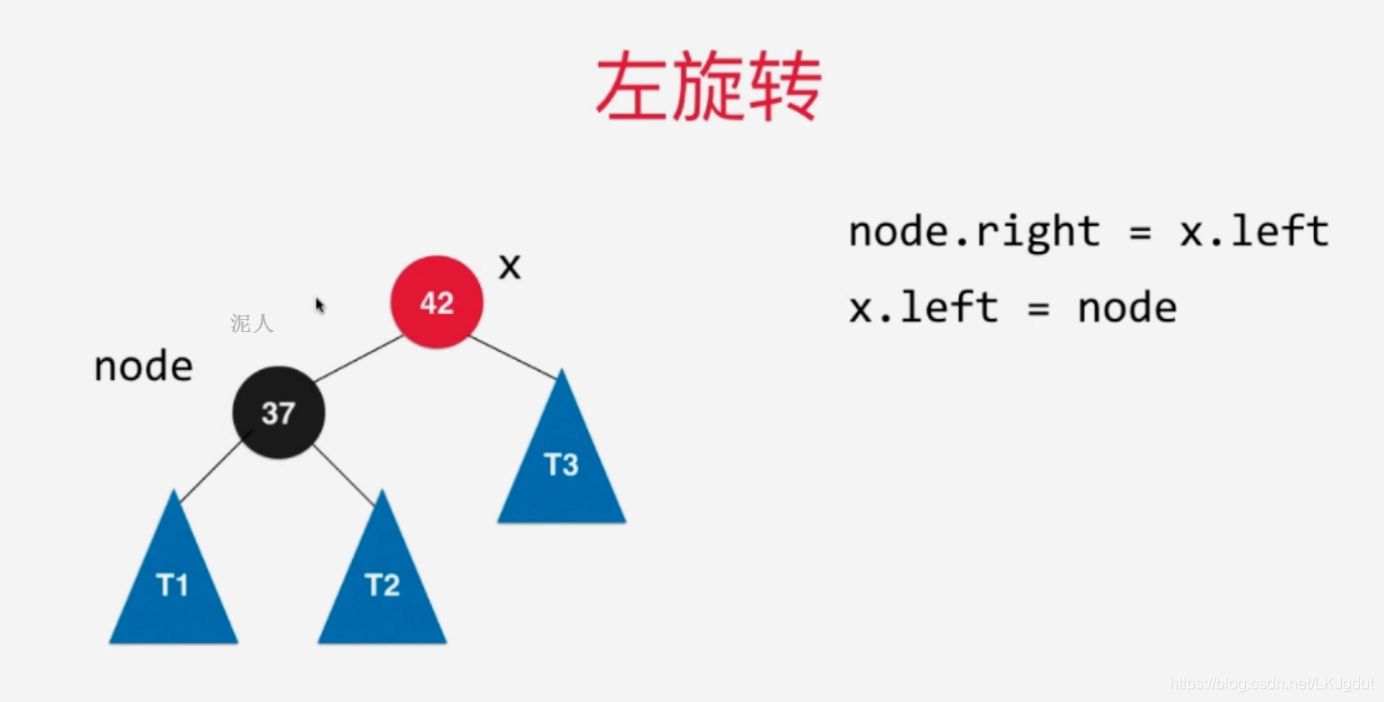
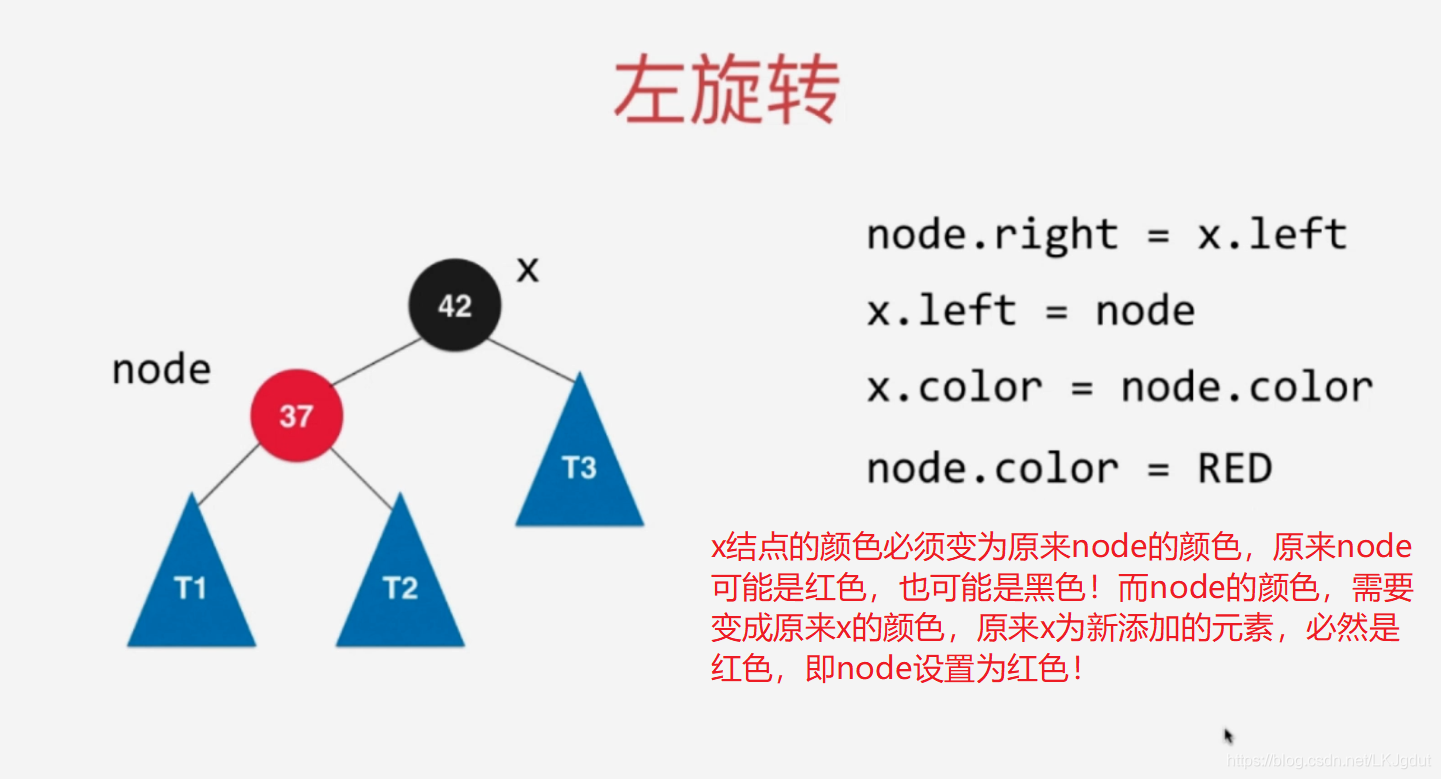
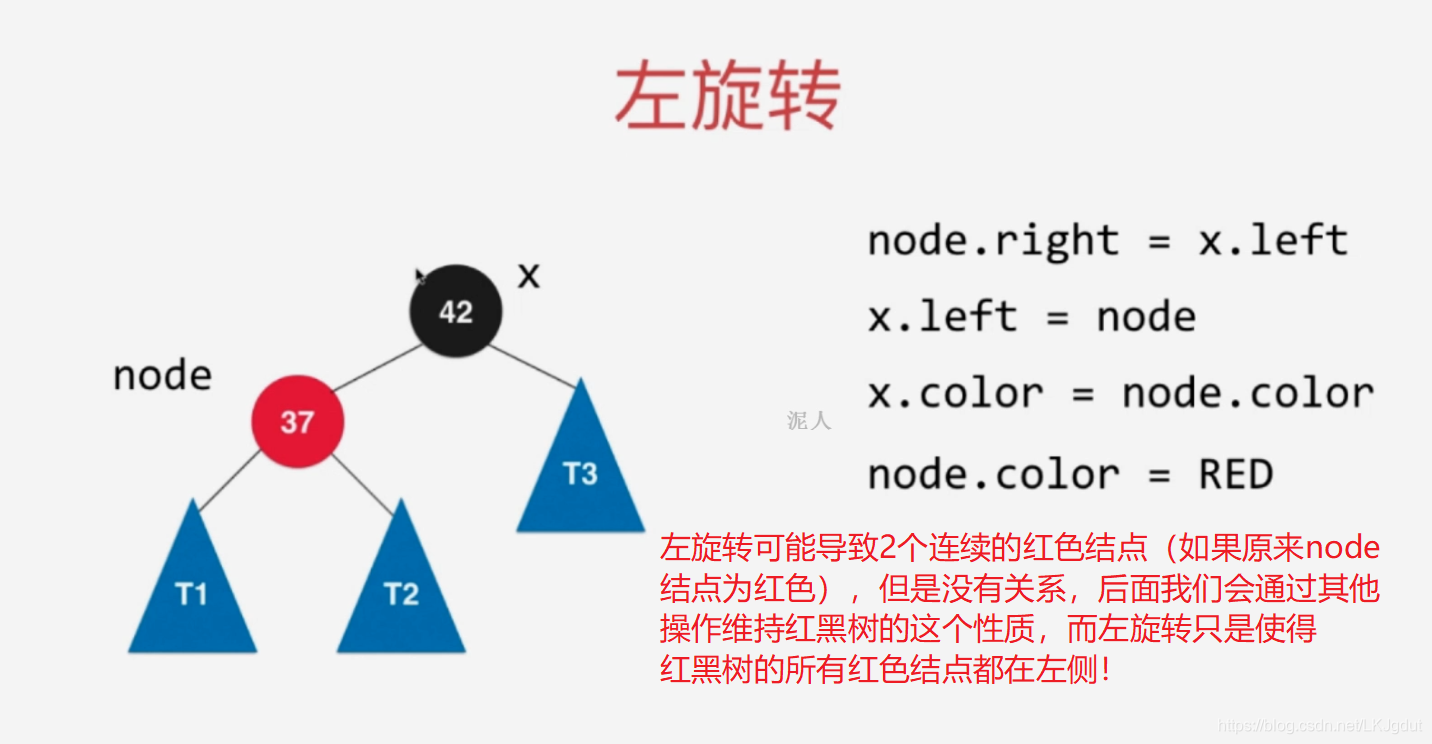
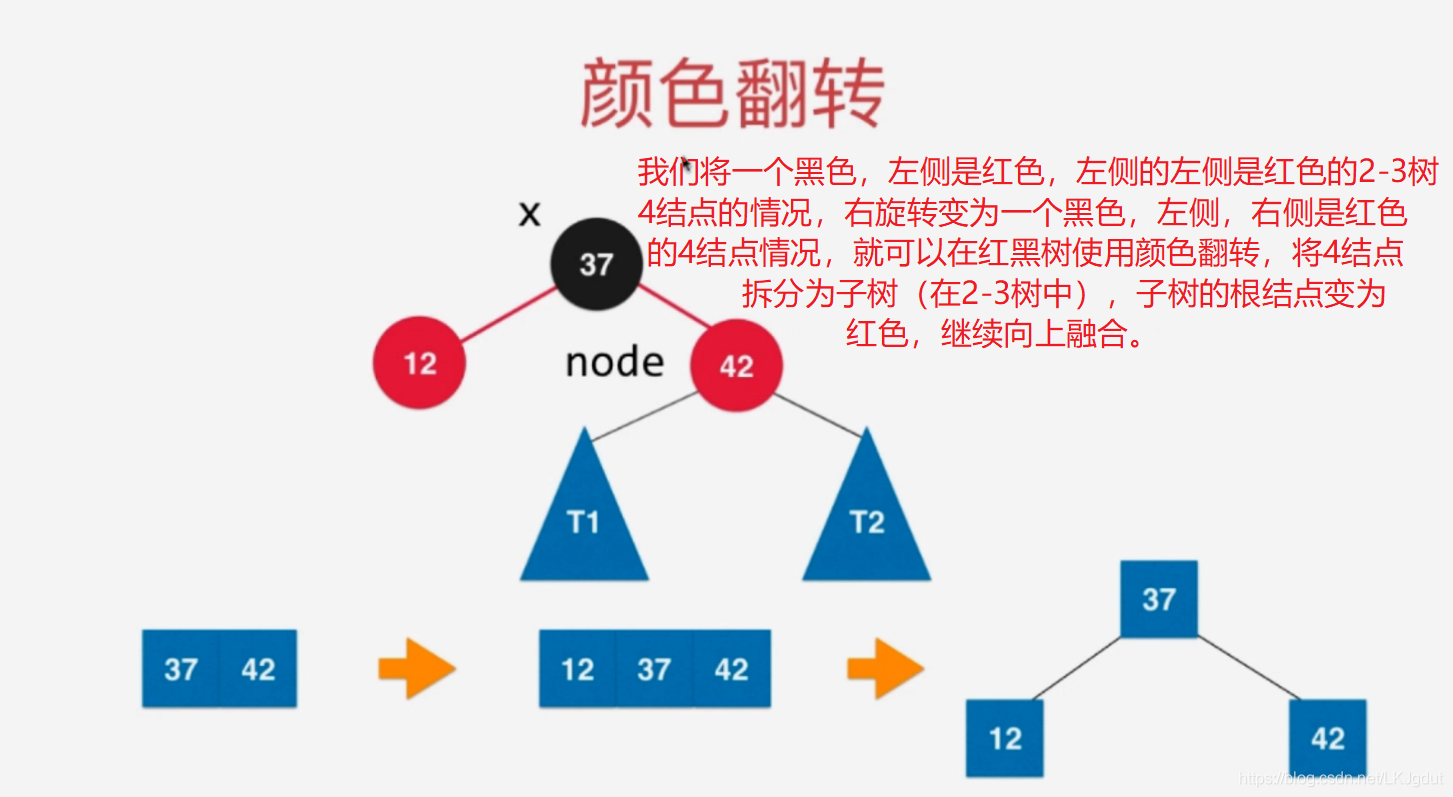
5）如果添加的新结点在黑色结点的右侧，而此时黑色结点左侧还有一个红色结点，添加之前，源节点对应2-3树中3结点，添加后，黑色结点左右两侧都是红色结点，对应2-3树的4结点。此时，2-3树需要将4结点拆分为子树，而红黑树中我们需要进行颜色翻转。




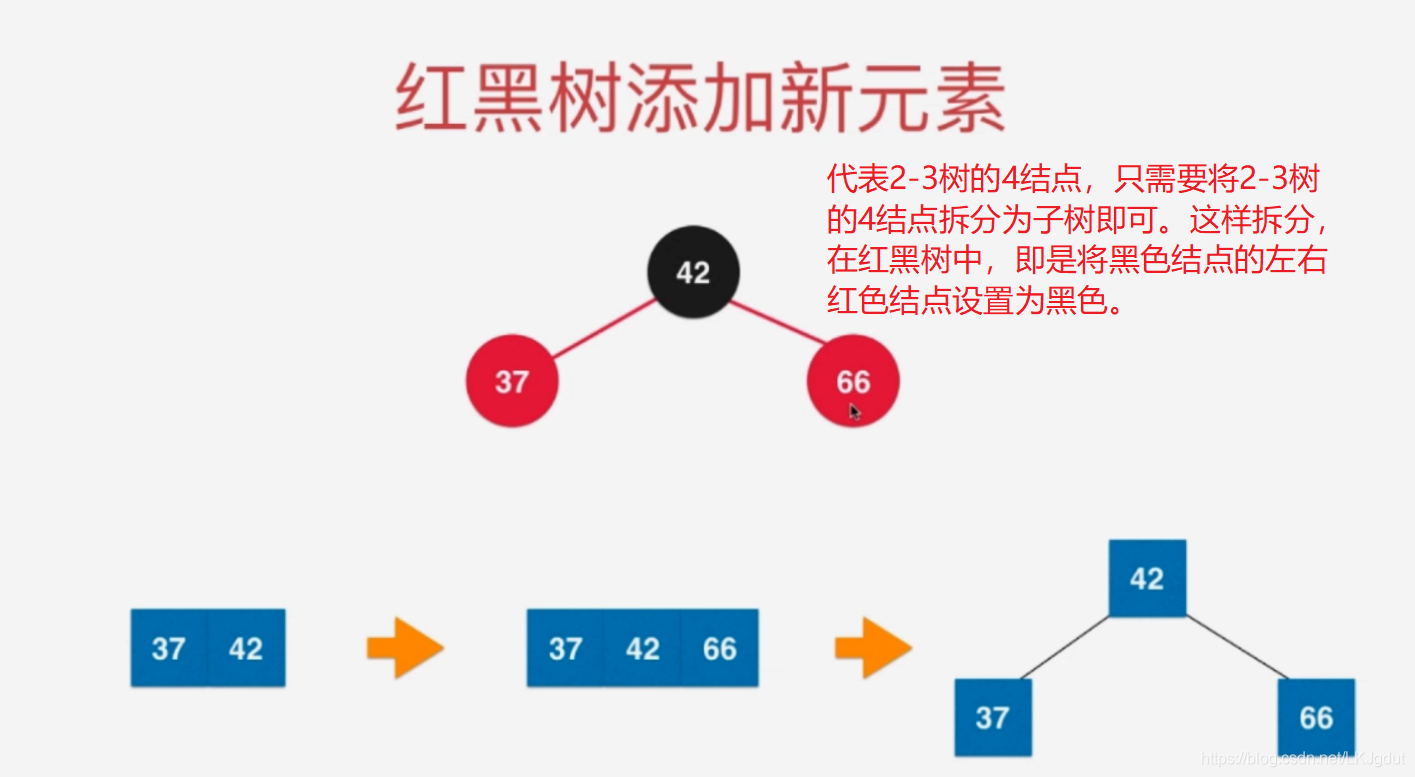
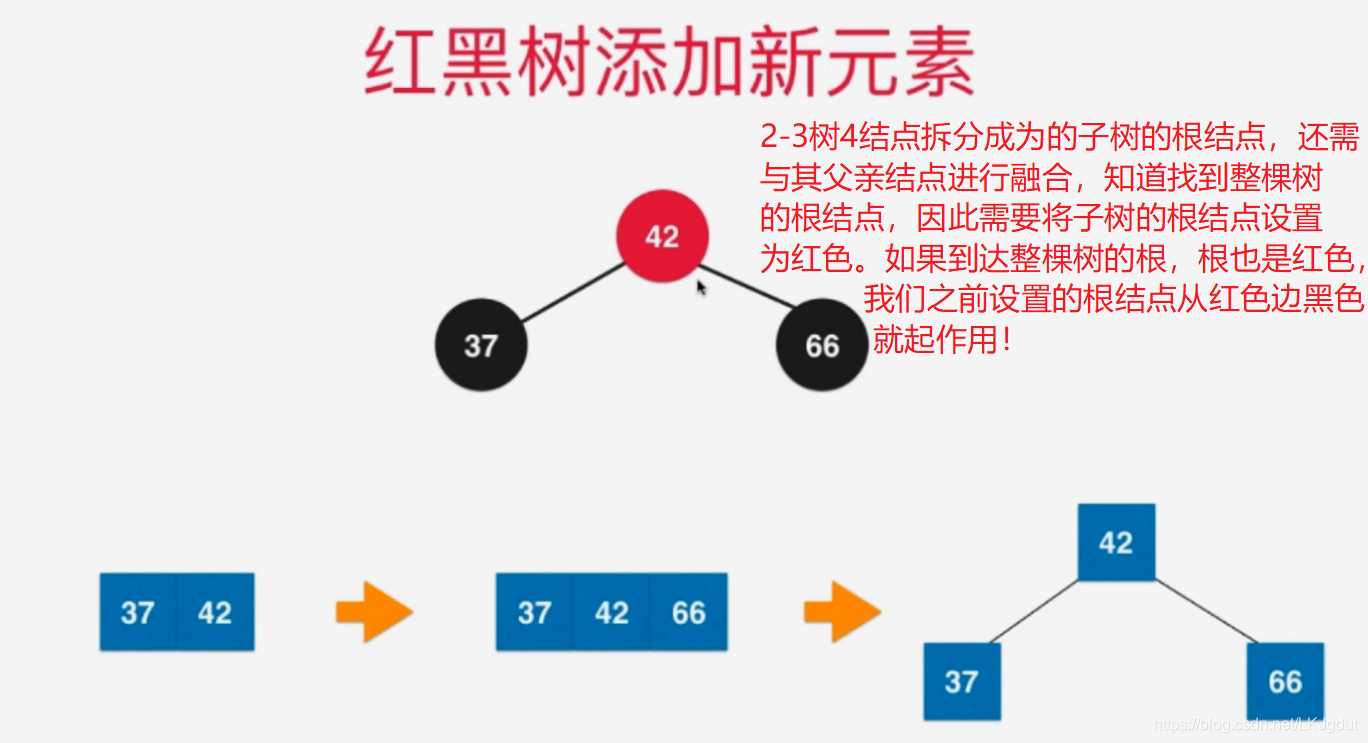
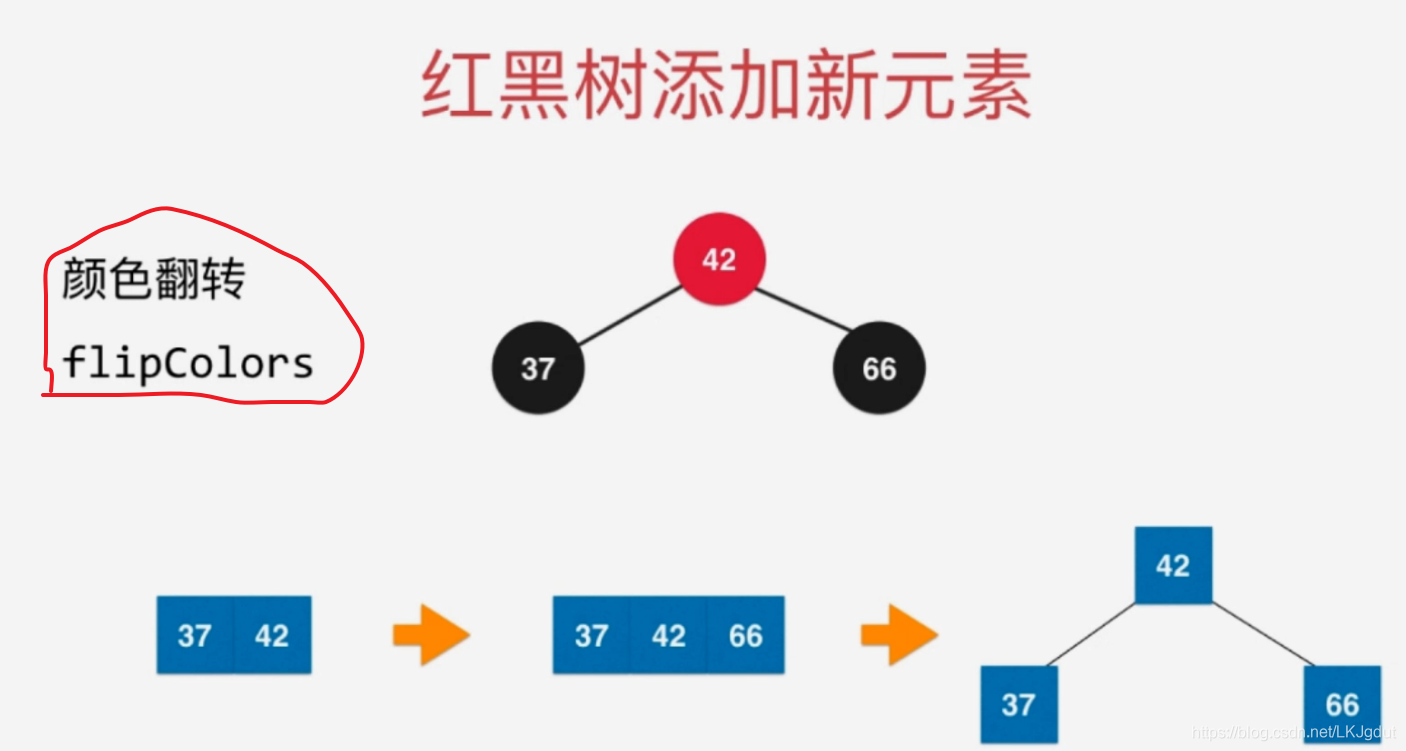
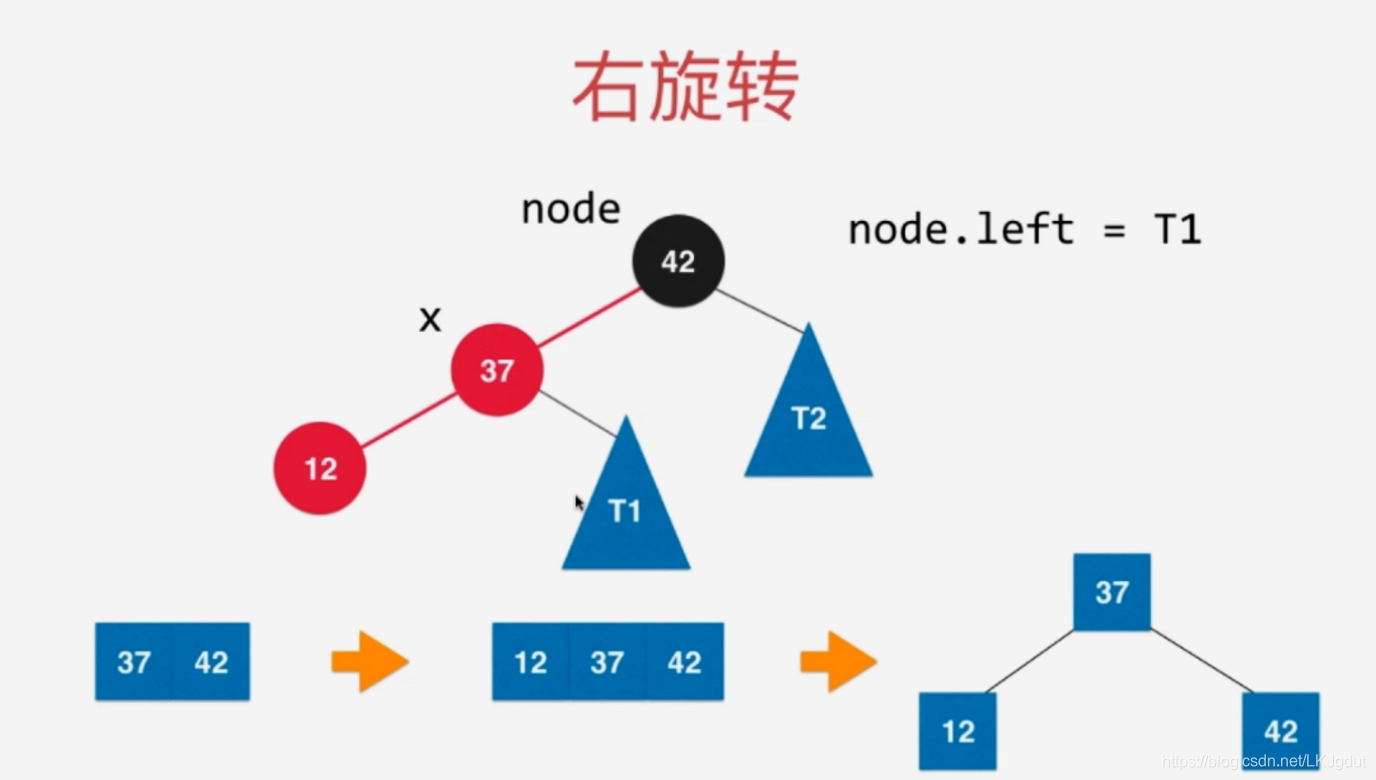
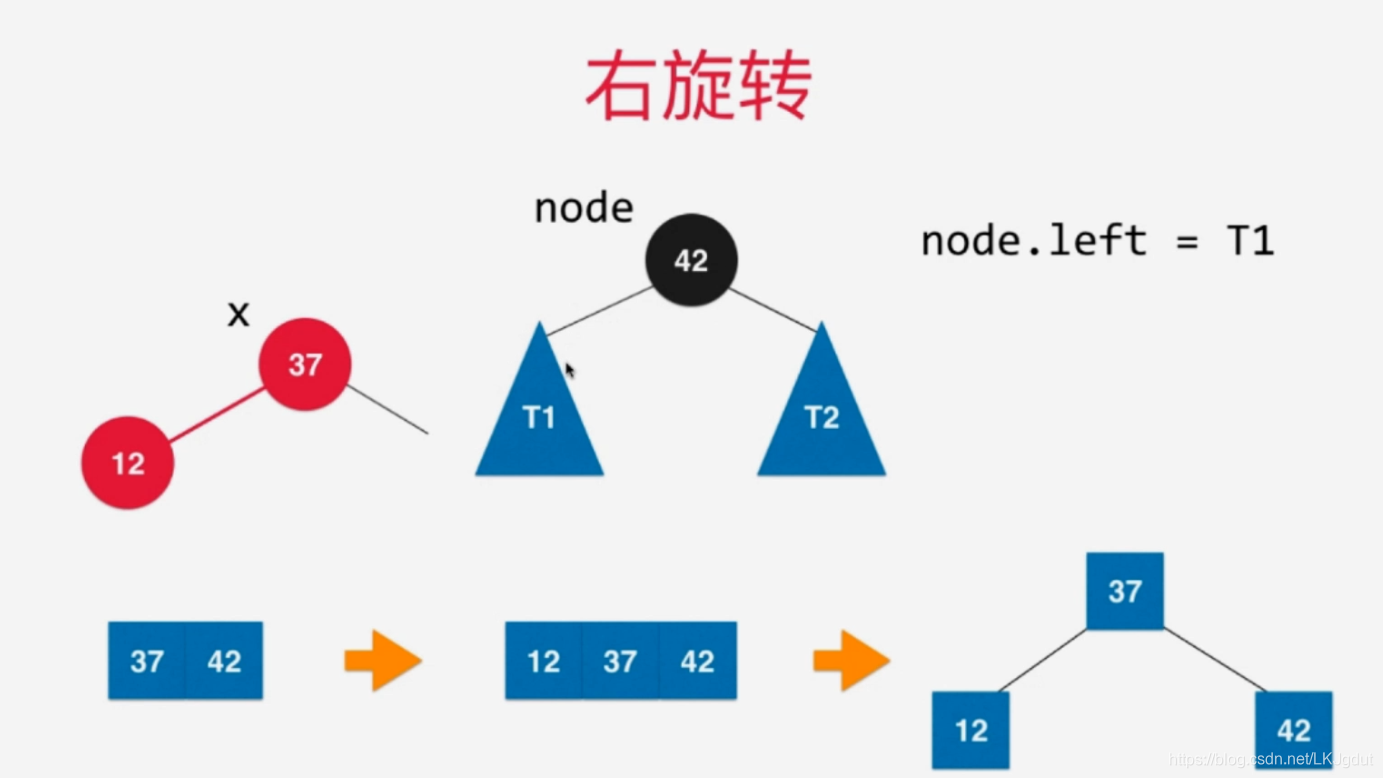
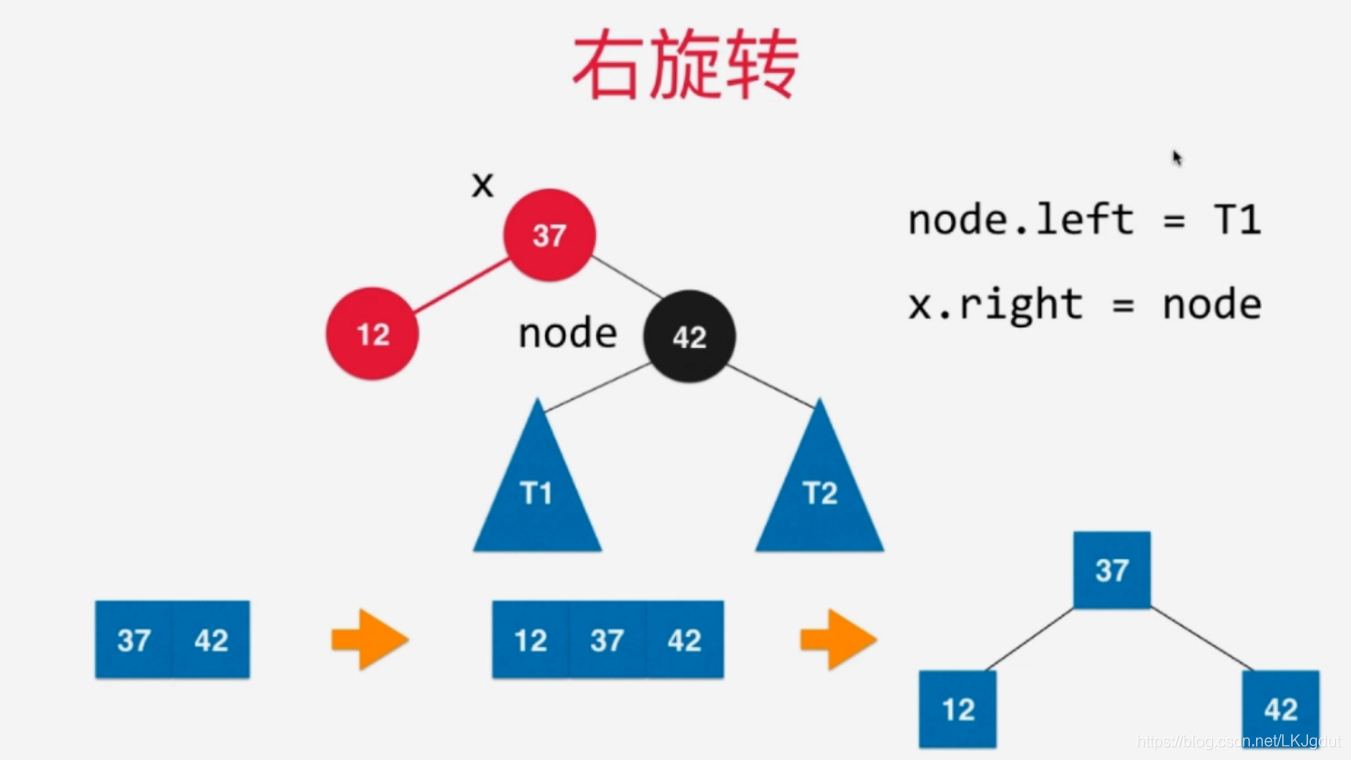
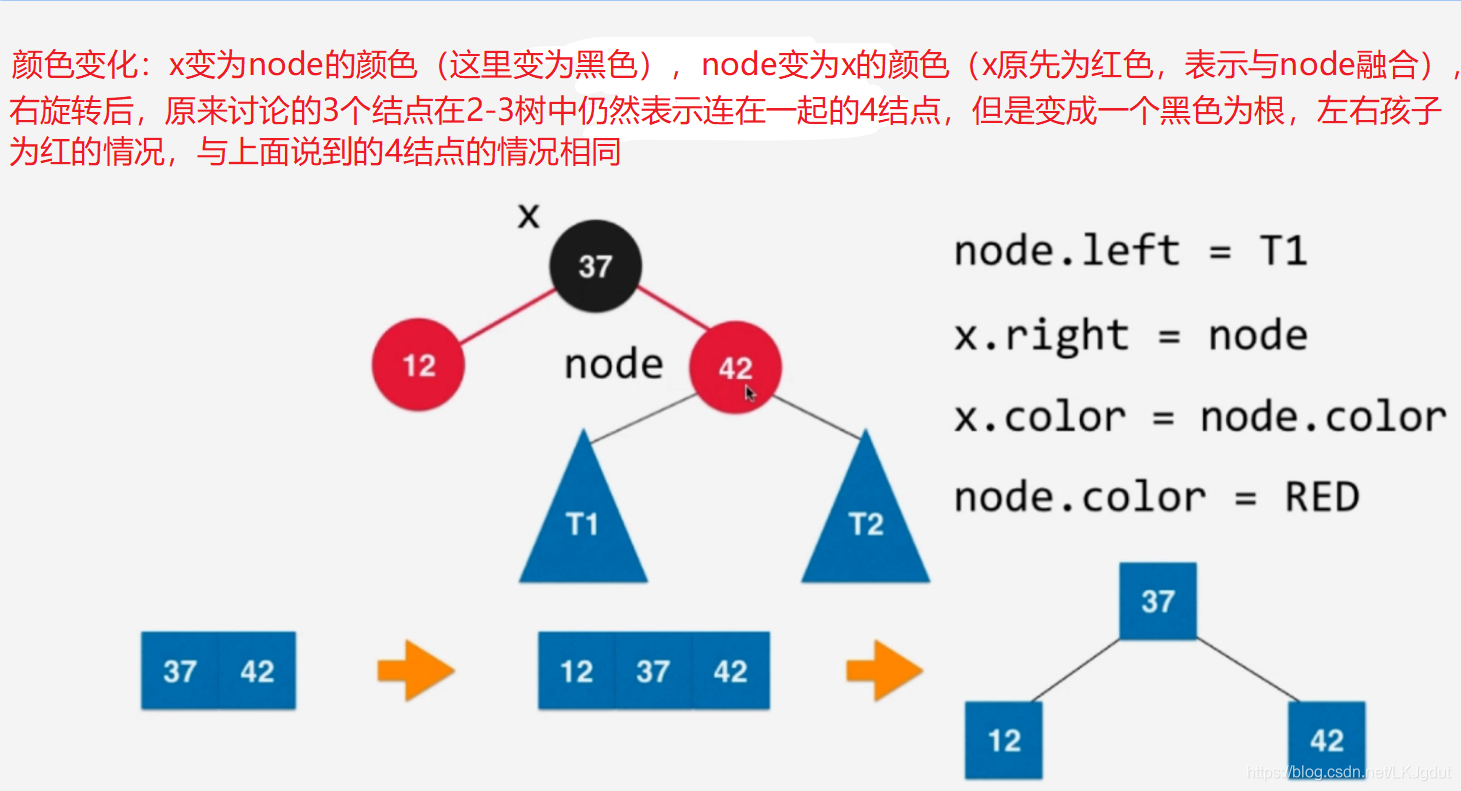
6）如果添加的新结点在黑色结点的左侧红色结点的左侧，此时黑色结点左侧为红色结点，黑色结点右侧是黑色结点，这样在2-3树中表示往3结点添加一个元素，时期变为4结点。同样要将4结点拆分为子树，红黑树中，我们则需要对黑色结点进行右旋转（顺时针）。

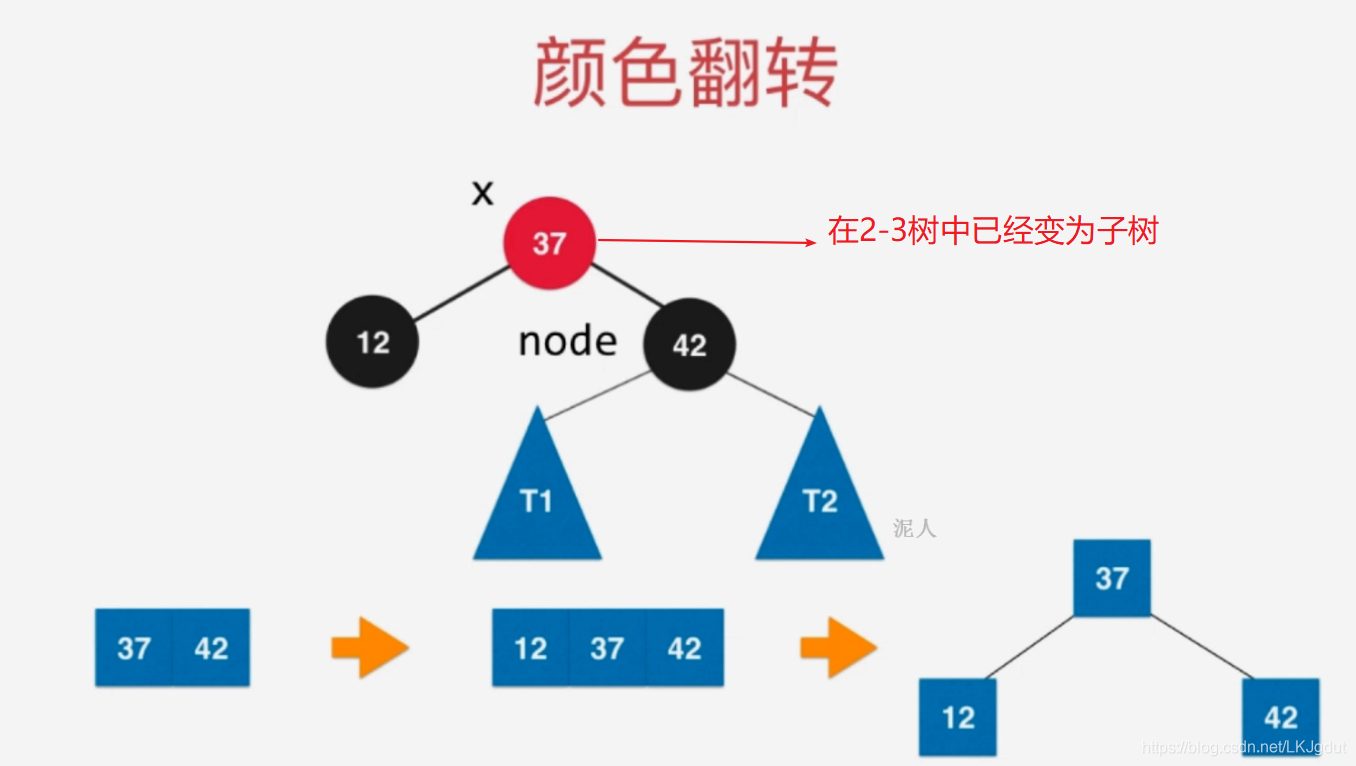
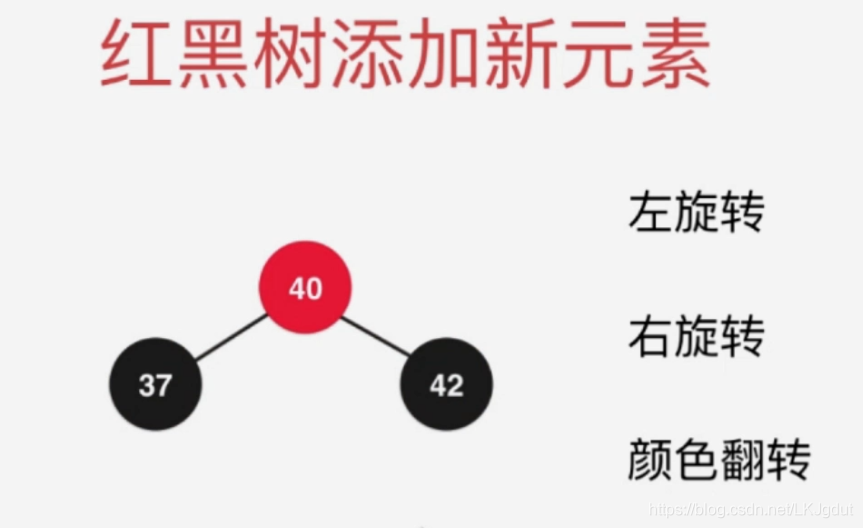
6、红黑树中添加新的元素
  上面少说一种情况，就是在红色结点的右边添加新的红色结点：




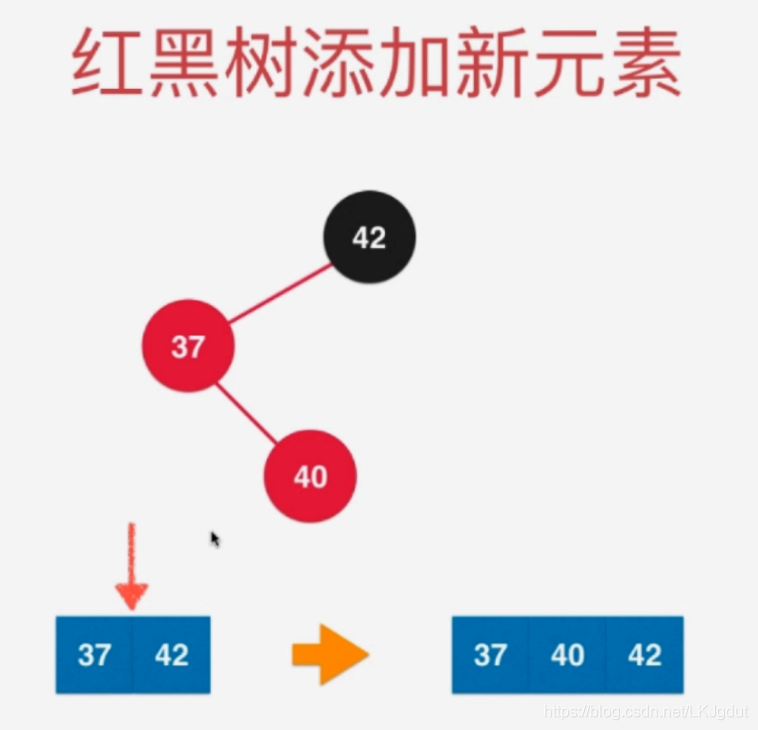
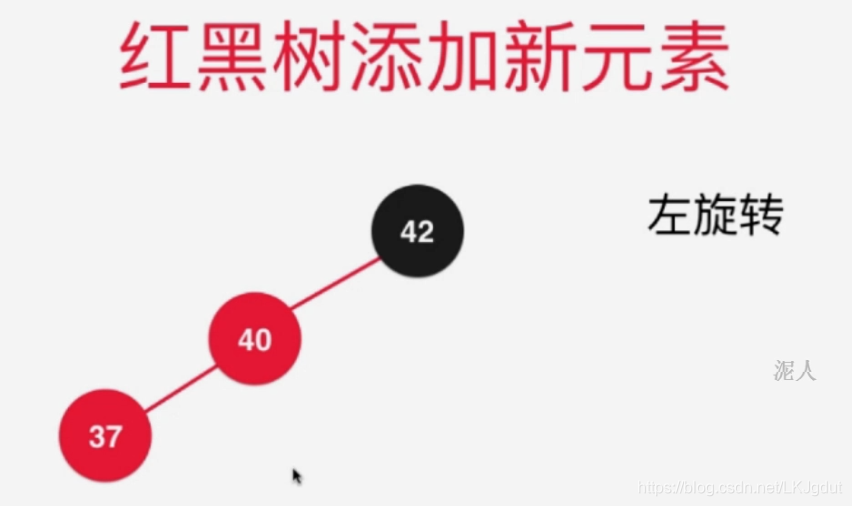
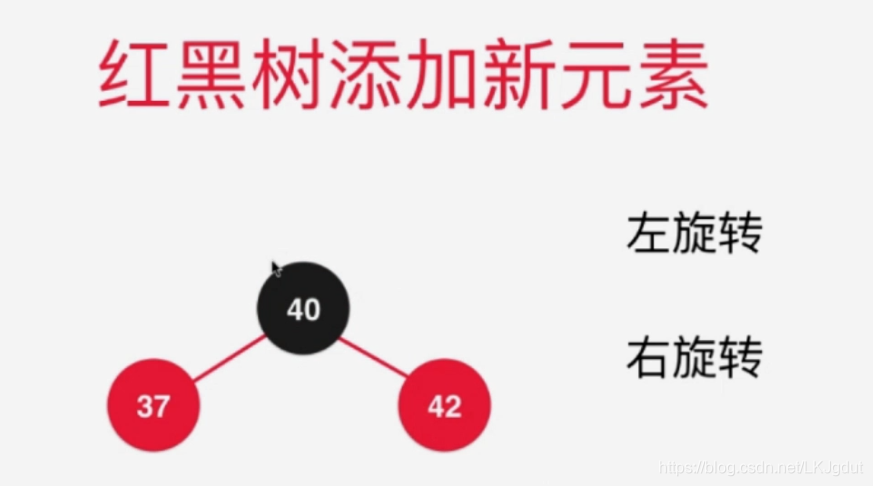
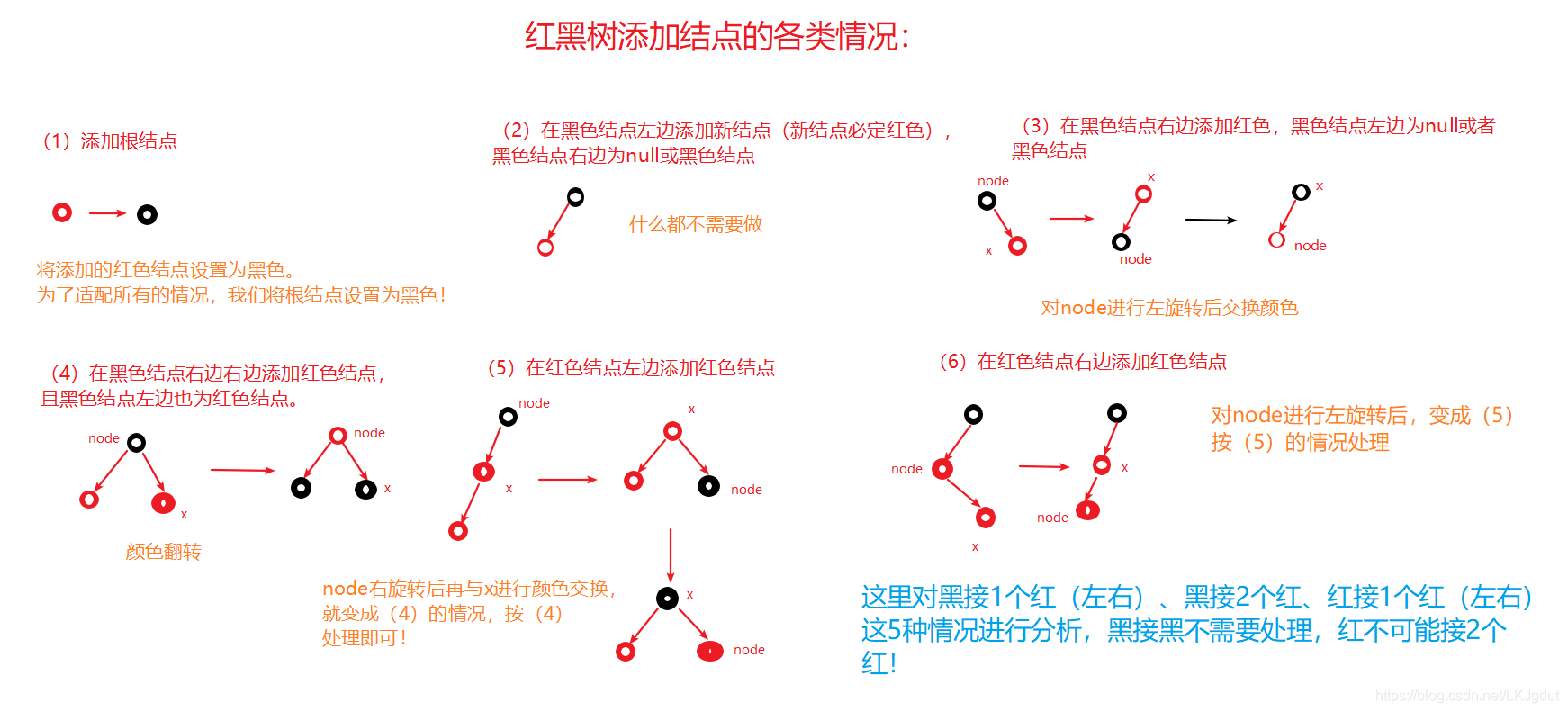
  红黑树的各类情况处理方法：


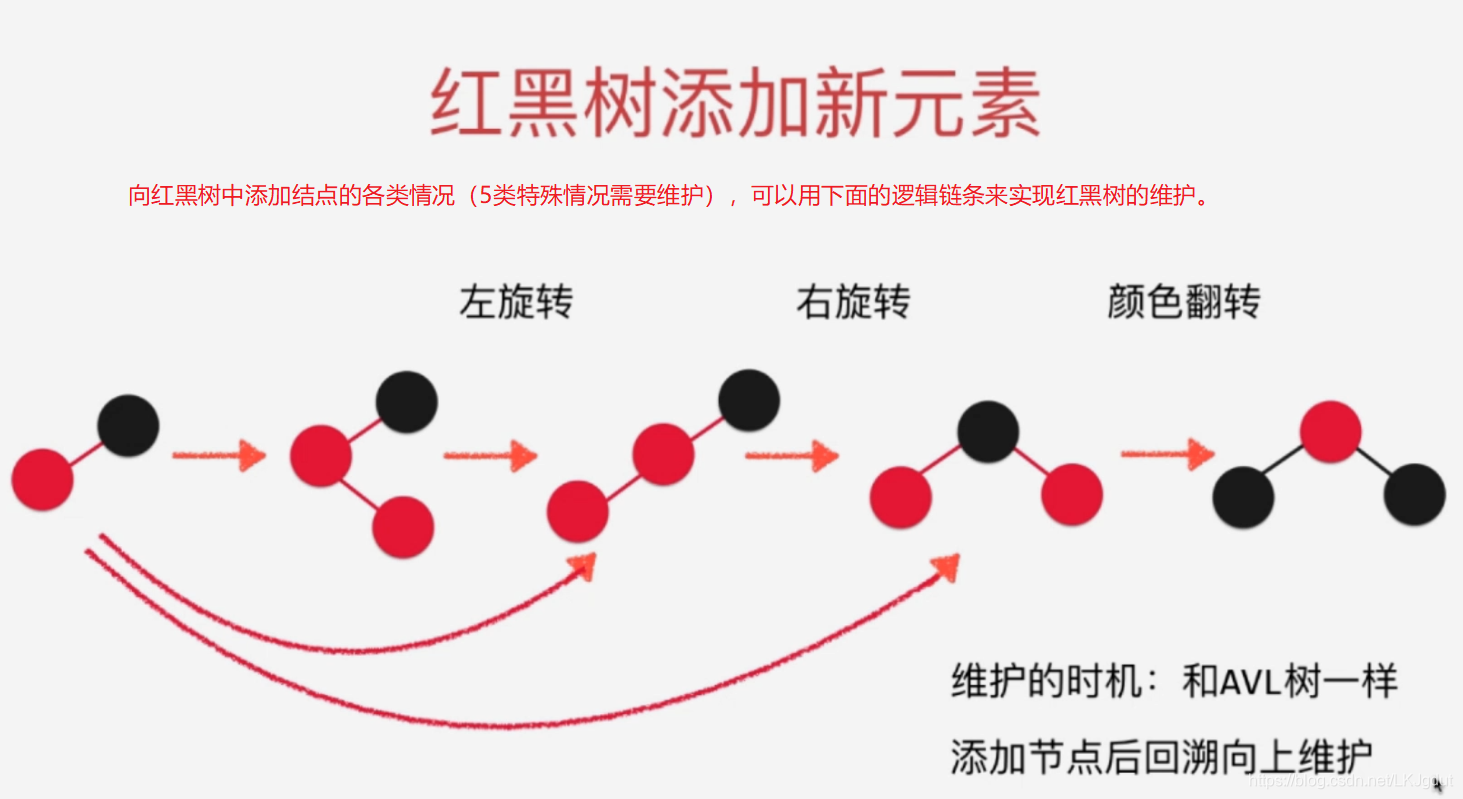
  我们在红黑树中进行平衡维护的时候，如上图，应该从左到右进行判断：
1）如果当前结点的右孩子结点为红色（当前结点可以是红色(2-3树4结点)，也可以是黑色(2-3树3结点)），且左孩子结点为黑色，则将当前结点左旋转；
2）如果当前结点的左孩子以及左孩子的左孩子都是红色的，则对当前结点进行右旋转；
3）如果当前结点的左右孩子都是红色，则进行颜色翻转；
4）对于另外2种对应2-3树中3结点的情况，黑节点左孩子为红结点，右孩子为黑结点，不需要操作；黑结点右孩子为红结点，左孩子为黑结点，包含在（1）中；

  红黑树的代码如下：

package com.lkj;

import java.util.ArrayList;

/**
红黑树也是基于二分搜索树实现的！
 */
public class RBTree<K extends Comparable<K>, V> {
   
   

    //为了避免记红色与黑色的Boolean值，定义2个厂里
    public static final boolean RED =