string 常见题目详解——仅仅反转字母找字符串第一次出现的字符字符串最后单词长度验证回文串字符串相加-优快云博客

1.题目一：仅仅反转字母

题目描述：
给定一个字符串，返回“反转后的”字符串，其中不是字母的字符都保留在原地，而所有字母的位置发生反转。

示例：
输入：“a-bC-dEf-ghIj”
输出：“j-Ih-gfE-dCba”

思路：
使用双指针法，分别从字符串的首尾开始向中间遍历。当两个指针都指向字母时，交换这两个字母的位置；若指针指向的不是字母，则将该指针向中间移动，直到找到字母为止。不断重复这个过程，直到两个指针相遇或交叉。

class Solution {
public:
    string reverseOnlyLetters(string s) {
    int n=s.size();
        int left=0;
        int right =n-1;
        while(left<right)
        {
            if(left<right&& !std::isalpha(s[left]))
            {
                ++left;
            }
             if(left<right&& !std::isalpha(s[right]))
            {
                --right;
            }
            if(left>=right)
            {
                break;
            }

            std::swap(s[left], s[right]);  
            ++left;  
            --right;  
  
        }
        return s;
    }
};

整体思路

使用双指针法，分别从字符串的首尾开始向中间遍历。当两个指针都指向字母时，交换这两个字母的位置；若指针指向的不是字母，则将该指针向中间移动，直到找到字母为止。不断重复这个过程，直到两个指针相遇或交叉。

具体步骤

1. 初始化变量

int n = s.size();
int left = 0;
int right = n - 1;

n：获取字符串 s 的长度。
left：左指针，初始化为字符串的起始位置（索引为 0）。
right：右指针，初始化为字符串的末尾位置（索引为 n - 1）。

2. 进入循环

while (left < right)

使用 while 循环，只要 left 小于 right，就继续执行循环体。这保证了两个指针不会交叉。

3. 移动左指针

if (left < right && !std::isalpha(s[left]))
{
    ++left;
}

std::isalpha 是 C++ 标准库中的函数，用于判断一个字符是否为字母。
当 left 小于 right 且 s[left] 不是字母时，将 left 指针右移一位，继续寻找下一个字母。

4. 移动右指针

if (left < right && !std::isalpha(s[right]))
{
    --right;
}

同理，当 left 小于 right 且 s[right] 不是字母时，将 right 指针左移一位，继续寻找下一个字母。

5. 检查指针位置

if (left >= right)
{
    break;
}

在移动完左右指针后，再次检查 left 和 right 的位置。如果 left 大于等于 right，说明已经完成了所有字母的交换，跳出循环。

6. 交换字母

std::swap(s[left], s[right]);
++left;
--right;

当左右指针都指向字母时，使用 std::swap 函数交换这两个字母的位置。
交换完成后，将 left 指针右移一位，right 指针左移一位，继续寻找下一对需要交换的字母。

7. 返回结果

return s;

循环结束后，返回反转字母后的字符串 s。

复杂度分析

时间复杂度：\(O(n)\)，其中 n 是字符串的长度。因为只需要遍历字符串一次。
空间复杂度：\(O(1)\)，只使用了常数级的额外空间。

示例

假设输入字符串 s = "a-bC-dEf-ghIj"，经过上述步骤处理后，输出结果为 "j-Ih-gfE-dCba"。非字母字符 - 的位置保持不变，而字母的位置被反转。

2.找字符串中第一个只出现一次的字符

给定一个字符串 s ，找到 它的第一个不重复的字符，并返回它的索引 。如果不存在，则返回 -1 。

示例 1：

输入: s = "leetcode"
输出: 0

示例 2:

输入: s = "loveleetcode"
输出: 2

示例 3:

输入: s = "aabb"
输出: -1

提示:

1 <= s.length <= 105
s 只包含小写字母

class Solution {
public:
    int firstUniqChar(string s) {
        int a[26]={0};
        for(auto ch: s)
        {
            a[ch-'a']++;
        }
        for(size_t i=0;i<s.size();++i)
        {
           if( a[s[i]-'a']==1)
           return i;
        }
        return -1;
    }
};

这段代码定义了一个 Solution 类，其中的 firstUniqChar 函数用于找出字符串 s 中第一个只出现一次的字符，并返回它的索引。若不存在这样的字符，则返回 -1。下面详细阐述其实现思路：

整体思路

该函数借助数组来统计字符串中每个字母的出现次数，接着再次遍历字符串，找出第一个出现次数为 1 的字符的索引。

具体步骤

1. 初始化计数数组

int a[26] = {0};

创建一个长度为 26 的整型数组 a，用于记录字符串 s 中每个小写字母的出现次数。数组的每个元素对应一个小写字母，a[0] 对应字母 'a'，a[1] 对应字母 'b'，依此类推，a[25] 对应字母 'z'。数组初始化为全 0，表示所有字母的初始出现次数都为 0。

2. 统计每个字母的出现次数

for (auto ch : s)
{
    a[ch - 'a']++;
}

使用范围 for 循环遍历字符串 s 中的每个字符 ch。通过 ch - 'a' 计算出该字符在数组 a 中对应的索引位置，然后将该位置的元素值加 1。例如，如果 ch 是 'a'，ch - 'a' 的结果为 0，那么 a[0] 的值会加 1；如果 ch 是 'b'，ch - 'a' 的结果为 1，a[1] 的值会加 1，以此类推。

3. 查找第一个只出现一次的字符

for (size_t i = 0; i < s.size(); ++i)
{
    if (a[s[i] - 'a'] == 1)
        return i;
}

使用普通的 for 循环再次遍历字符串 s。对于每个字符 s[i]，计算其在数组 a 中对应的索引位置 s[i] - 'a'，检查该位置的元素值是否为 1。如果为 1，说明该字符只出现了一次，返回其索引 i。

4. 若未找到则返回 -1

return -1;

如果遍历完整个字符串都没有找到只出现一次的字符，说明不存在这样的字符，返回 -1。

复杂度分析

时间复杂度：\(O(n)\)，其中 n 是字符串 s 的长度。需要遍历字符串两次，每次遍历的时间复杂度都是 \(O(n)\)，因此总的时间复杂度为 \(O(n)\)。
空间复杂度：\(O(1)\)。虽然使用了一个长度为 26 的数组，但数组的大小是固定的，不随字符串长度的变化而变化，因此空间复杂度为常数级，即 \(O(1)\)。

示例

假设输入字符串 s = "loveleetcode"，程序会先统计每个字母的出现次数，然后在第二次遍历中找到第一个只出现一次的字母 'v'，其索引为 2，最终返回 2。

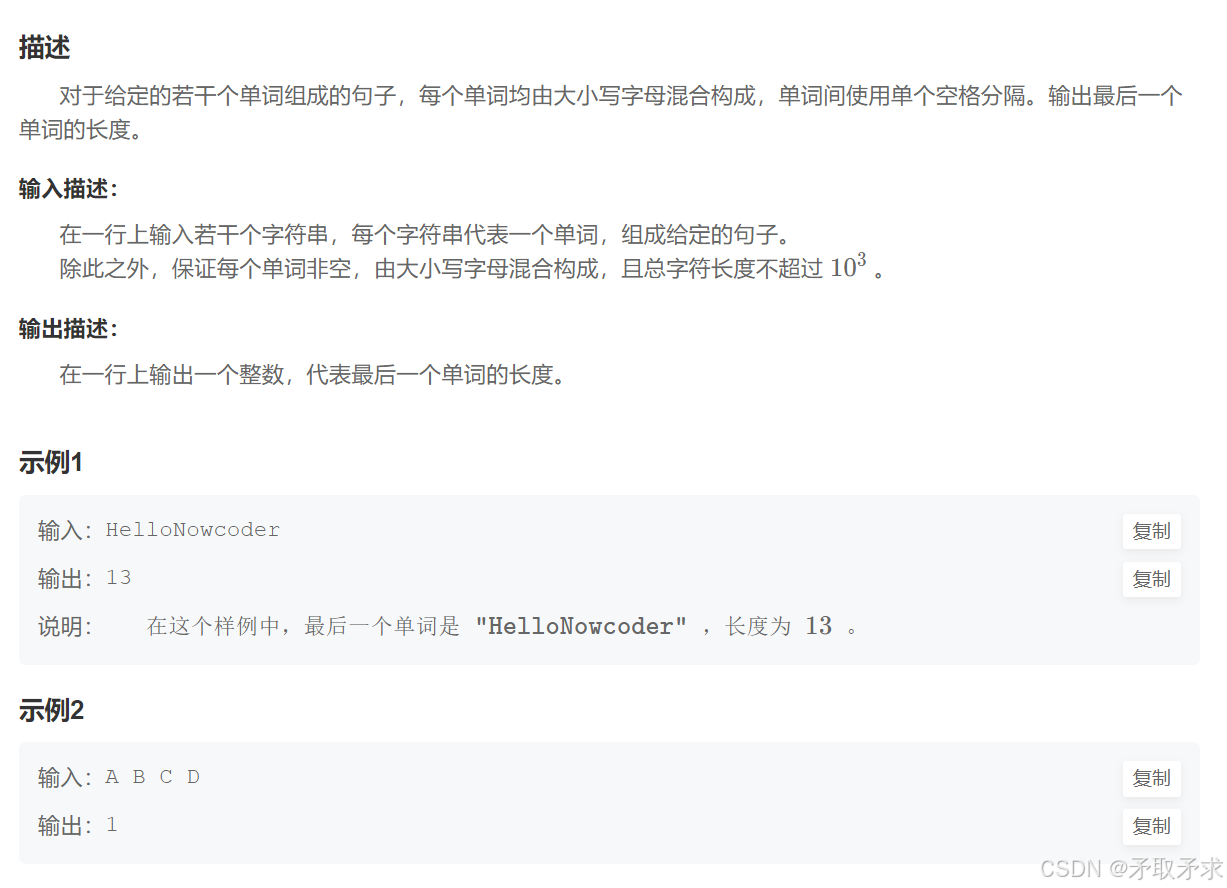
3.字符串最后一个单词的长度

第一种

#include <iostream>
#include <string>
using namespace std;

int main() {
    string s;
    getline(cin, s);
    int length = 0;
    for (int i = s.size() - 1; i >= 0; --i) {
        if (s[i] != ' ') {
            length++;
        } else {
            break;
        }
    }
    cout << length << endl;
    return 0;
}

第二种

#include <iostream>
using namespace std;
#include <string>
int main()
{
    string str;
    getline(cin,str);
    std::string::reverse_iterator rit=str.rbegin();
    int lenght=0;
    while (rit!=str.rend()&&*rit!=' ')
    {
         ++rit;
         ++lenght;
    }
   
    std::cout << lenght;
    return 0;
}

代码解释

输入字符串：

std::string str;
std::getline(std::cin, str);

定义一个 std::string 类型的变量 str 用于存储输入的字符串，使用 std::getline 函数读取一整行输入，包括空格，将其存入 str 中。

初始化反向迭代器：

std::string::reverse_iterator rit = str.rbegin();

创建一个反向迭代器 rit，并将其初始化为字符串 str 的反向起始迭代器 rbegin()，这样后续可以从字符串的末尾开始向前遍历。

跳过末尾的空格：

while (rit != str.rend() && *rit == ' ') {
    ++rit;
}

使用 while 循环，只要迭代器 rit 没有到达字符串反向的末尾 rend() 并且当前迭代器指向的字符是空格，就将迭代器向前移动一位（++rit），以此跳过字符串末尾可能存在的连续空格。

统计最后一个单词的长度：

while (rit != str.rend() && *rit != ' ') {
    ++length;
    ++rit;
}

继续使用 while 循环，在迭代器 rit 没有到达字符串反向的末尾 rend() 并且当前迭代器指向的字符不是空格的情况下，每次将长度计数器 length 加 1，同时将迭代器向前移动一位（++rit），直到遇到空格或者到达字符串的反向开头，此时 length 即为最后一个单词的长度。

输出结果：

std::cout << length << std::endl;

将统计得到的最后一个单词的长度输出到控制台。

4.验证回文串

class Solution {
public:
    bool isPalindrome(string s) {
         for (char& c : s) 
         {
            c = tolower(c);
        }
        int left=0;
        int right=s.size()-1;
        while(left<right)
        {
            while(left<right&&! isalnum(s[left]))
            {
                ++left;
            }
            while(left<right&& !isalnum(s[right]))
            {
                --right;
            }
        
            if(s[left]!=s[right])
            {
                return false;
            }
            right--;
            left++;
        }
        return true;
    }
};

代码详细分析

1. 字符转换

for (char& c : s) 
{
    c = tolower(c);
}

此部分借助范围 for 循环遍历字符串 s 中的每个字符。
tolower(c) 函数把字符 c 转换为小写形式，再将转换后的字符重新赋值给 c，这样就能保证后续比较时不区分大小写。

2. 双指针初始化

int left = 0;
int right = s.size() - 1;

left 指针初始化为 0，指向字符串的起始位置。
right 指针初始化为 s.size() - 1，指向字符串的末尾位置。

3. 双指针遍历

while (left < right)

使用 while 循环，只要 left 小于 right 就持续循环，以此从字符串两端向中间进行比较。

4. 跳过非字母数字字符

while (left < right &&! isalnum(s[left]))
{
    ++left;
}
while (left < right &&! isalnum(s[right]))
{
    --right;
}

第一个 while 循环从左向右移动 left 指针，跳过所有非字母数字字符，直到 left 指向字母或数字字符，或者 left 与 right 相遇。
第二个 while 循环从右向左移动 right 指针，跳过所有非字母数字字符，直到 right 指向字母或数字字符，或者 right 与 left 相遇。
为什么不用if（）当有连续多个空怎么办，if()只跳过一个

5. 字符比较

if (s[left] != s[right])
{
    return false;
}

当 left 和 right 都指向字母或数字字符时，比较这两个字符是否相等。
若不相等，说明该字符串不是回文串，返回 false。

6. 移动指针

right--;
left++;

若当前比较的字符相等，将 left 指针右移一位，right 指针左移一位，继续比较下一对字符。

7. 返回结果

return true;

若整个循环结束后都没有发现不相等的字符，说明该字符串是回文串，返回 true。

复杂度分析

时间复杂度：\(O(n)\)，其中 n 是字符串的长度。因为每个字符最多被访问两次。
空间复杂度：\(O(1)\)，只使用了常数级的额外空间。

5.字符串相加

这段代码定义了一个 Solution 类，其中的 addStrings 函数实现了两个以字符串形式表示的非负整数相加的功能，最终返回相加结果的字符串形式。在处理大整数相加时，由于普通整数类型可能无法存储极大的数值，使用字符串来表示数字可以避免溢出问题。

代码详细分析

1. 变量初始化

int i = num1.size() - 1, j = num2.size() - 1, add = 0;
string tmp = "";

i 和 j 分别被初始化为 num1 和 num2 字符串的最后一个字符的索引，这是因为字符串表示的数字是从左到右为高位到低位，而加法运算通常从低位开始，所以从字符串末尾开始处理。
add 用于记录进位，初始化为 0。
tmp 是一个空字符串，用于存储相加过程中每一位的结果。

2. 循环条件

while (add != 0 || i >= 0 || j >= 0)

循环会持续进行，只要满足以下三个条件之一：

还有进位（add != 0）。
num1 还有未处理的字符（i >= 0）。
num2 还有未处理的字符（j >= 0）。

3. 获取当前位的数字

int x = i >= 0 ? num1[i] - '0' : 0;
int y = j >= 0 ? num2[j] - '0' : 0;

x 和 y 分别表示 num1 和 num2 当前位置的数字。
通过 num1[i] - '0' 和 num2[j] - '0' 将字符转换为对应的整数。如果 i 或 j 小于 0，说明对应的字符串已经处理完，此时将该位置的数字视为 0。

4. 计算当前位的和与进位

int tmp1 = x + y + add;
tmp.push_back(tmp1 % 10 + '0');
add = tmp1 / 10;

tmp1 是当前位的和，包括前一位的进位 add。
tmp1 % 10 得到当前位相加后的个位数，将其转换为字符（通过加 '0'）后添加到 tmp 字符串末尾。
tmp1 / 10 得到进位，更新 add 的值。

5. 指针移动

i -= 1;
j -= 1;

将 i 和 j 指针分别向前移动一位，以便处理下一位数字。

6. 反转结果字符串

reverse(tmp.begin(), tmp.end());

由于加法是从低位开始处理的，结果字符串 tmp 是逆序的，使用 reverse 函数将其反转，得到正确的顺序。

7. 返回结果

return tmp;

返回相加结果的字符串形式。

复杂度分析

时间复杂度：\(O(\max(m, n))\)，其中 m 和 n 分别是 num1 和 num2 的长度。因为需要逐位处理两个字符串，循环次数取决于较长的字符串。
空间复杂度：\(O(\max(m, n))\)，主要用于存储相加结果的字符串 tmp。

6. 反转字符串

6.1第一种

#include <string>
#include <algorithm>

class Solution {
public:
    std::string reverseStr(std::string s, int k) {
        for (int i = 0; i < s.size(); i += 2 * k) {
            // 处理前 k 个字符
            if (i + k <= s.size()) {
                std::reverse(s.begin() + i, s.begin() + i + k);
            } else {
                // 剩余字符少于 k 个，全部反转
                std::reverse(s.begin() + i, s.end());
            }
        }
        return s;
    }
};

代码解释

使用一个 for 循环，每次循环处理 2k 个字符，通过 i += 2 * k 来移动到下一组。
在循环内部，判断当前位置 i 加上 k 是否小于等于字符串的长度：
- 如果是，说明剩余字符数大于等于 k ，使用 std::reverse 函数反转从 s.begin() + i 到 s.begin() + i + k 的字符。
- 如果不是，说明剩余字符数小于 k ，使用 std::reverse 函数反转从 s.begin() + i 到 s.end() 的字符。
循环结束后，返回处理后的字符串 s 。