C语言入门笔记 第八讲【表达式详解】

一、本章重点

表达式求值

隐式类型转换

算术转换

操作符的属性

二、 表达式求值

表达式求值的顺序一部分是由操作符的优先级和结合性决定。

同样，有些表达式的操作数在求值的过程中可能需要转换为其他类型。

三、隐式类型转换（偷偷发生）

C的整型算术运算总是至少以缺少整型类型的精度来进行的。

为了获得这个精度，表达式中的字符和短整型操作数在使用之前被转换为普通整型，这种转换称为整型提升。

整型提升的意义：

表达式的整型运算要在CPU的相应运算器件内执行，CPU内整型运算器(ALU)的操作数的字节长度一般就是int的字节长度，同时也是CPU的通用寄存器的长度。

因此，即使两个char类型的相加，在CPU执行时实际上也要先转换为CPU内整型操作数的标准长度。

通用CPU（general-purpose CPU）是难以直接实现两个8比特字节直接相加运算（虽然机器指令中可能有这种字节相加指令）。所以，表达式中各种长度可能小于int长度的整型值，都必须先转换为int或unsigned int，然后才能送入CPU去执行运算。

 

//实例1
char a = 3;
//00000000000000000000000000000011
//00000011 - a

char b = 127;
//00000000000000000000000001111111
//01111111 - b

char c = a + b;
printf("%d",c);

 a、b的值被提升为普通整型，然后再执行加法运算。

这里a是字符型常量，只能存放一个字节，即8个bit位；

C语言规定，a发生截断，截取最低的8个bit位放入a中。

b同理。

相加：

//00000011 -a

//01111111 - b

为了获得精度，这时候对a,b进行整型提升。

加法运算完成之后，结果将被截断，然后再存储于c中。

如何进行整体提升呢？

整形提升是按照变量的数据类型的符号位来提升的。

a符号位是0，所以高位统统补0.

b同理。

然后再相加：

a:00000000000000000000000000000011

b:00000000000000000000000001111111

相加结果：00000000000000000000000010000010

再截断，放入c中。

c:10000010

但这不是最终结果，

c还需要进行整型提升，

但是我们发现c的高位，也就是符号位，是1

所以前面全部补充1.

这样就得到了c的补码，也即是c的真正存储的二进制码。

c:11111111111111111111111110000010-补码

11111111111111111111111100000001-反码

10000000000000000000000011111110-原码

即-126.

//负数的整形提升
char c1 = -1;
变量c1的二进制位(补码)中只有8个比特位：
1111111
因为 char 为有符号的 char
所以整形提升的时候，高位补充符号位，即为1
提升之后的结果是：
11111111111111111111111111111111
//正数的整形提升
char c2 = 1;
变量c2的二进制位(补码)中只有8个比特位：
00000001
因为 char 为有符号的 char
所以整形提升的时候，高位补充符号位，即为0
提升之后的结果是：
00000000000000000000000000000001
//无符号整形提升，高位补0

总结：负数整型提升高位补1，正数整型提升高位补0。 无符号数也补0。

 整形提升的例子-实例1:

//实例1
int main()
{
 char a = 0xb6;
 short b = 0xb600;
 int c = 0xb6000000;
 if(a==0xb6)
 printf("a");
 if(b==0xb600)
 printf("b");
 if(c==0xb6000000)
 printf("c");
 return 0;
}

 实例1中的a,b要进行整形提升,但是c不需要整形提升

a中，一个16进制数需要4位，两个16进制数需要8位，刚好凑出一个字节，所以可以表示一个字符；

a:10110110

需要整型提升

高位补1；

b同理。

a,b整形提升之后,变成了负数,

所以表达式 a==0xb6 , b==0xb600 的结果是假,但是c不发生整形提升,则表达式 c==0xb6000000 的结果是真

输出结果是c。

实例2：

//实例2
int main()
{
 char c = 1;
 printf("%u\n", sizeof(c));
 printf("%u\n", sizeof(+c));
 printf("%u\n", sizeof(!c));
 return 0;
}

结果：1 4 1

实例2中的,c只要参与表达式运算,就会发生整形提升,表达式 +c ,就会发生提升,所以 sizeof(+c) 是4个字节.

表达式 -c 也会发生整形提升,所以 sizeof(-c) 是4个字节,但是 sizeof(c) ,就是1个字节。

四、算术转换

如果某个操作符的各个操作数属于不同的类型，那么除非其中一个操作数的转换为另一个操作数的类型，否则操作就无法进行。下面的层次体系称为寻常算术转换。

如果某个操作数的类型在上面这个列表中排名较低，那么首先要转换为另外一个操作数的类型后执行运算。

如同时出现unsigned int 和 int，

那么我们需要首先把int转换成unsigned int.

警告： 但是算术转换要合理，要不然会有一些潜在的问题。

float f = 3.14;
int num
比特科技 = f;//隐式转换，会有精度丢失

五、操作符的属性

 复杂表达式的求值有三个影响的因素。

1. 操作符的优先级

2. 操作符的结合性

3. 是否控制求值顺序。

两个相邻的操作符先执行哪个？取决于他们的优先级。

如果两者的优先级相同，取决于他们的结合性（先左后右还是先右后左）。

是否控制求值顺序：

如逻辑与，它左边为假，后面就不算了。

操作符优先级(从上到下，从高到低）

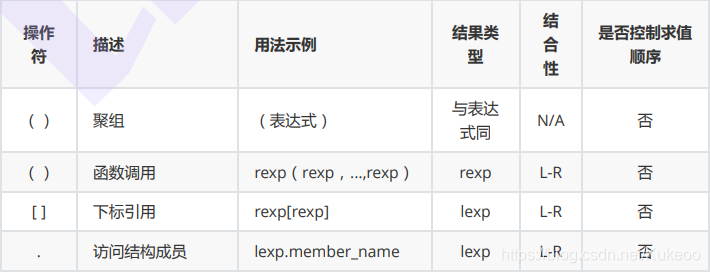
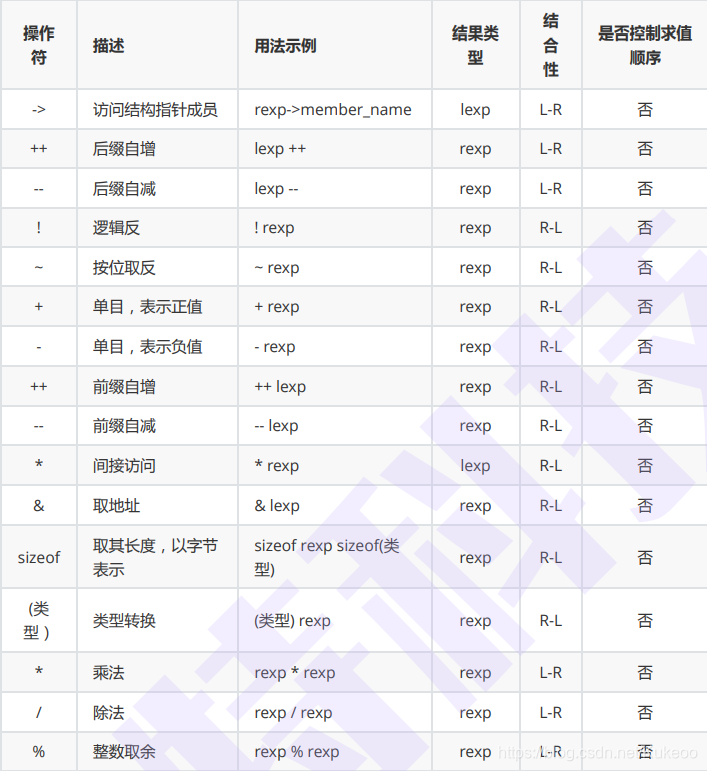
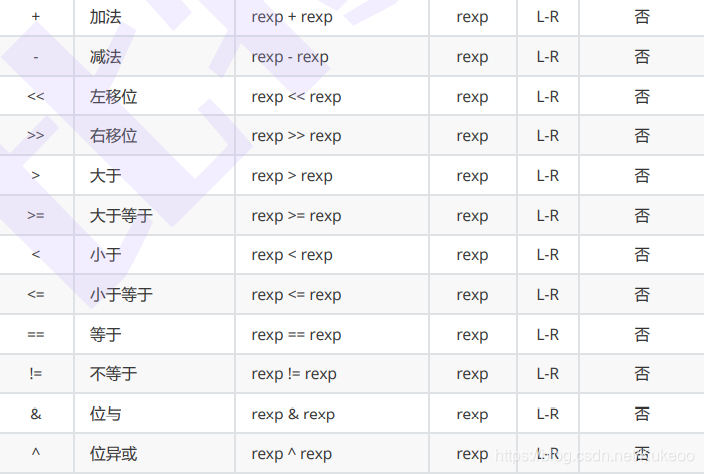
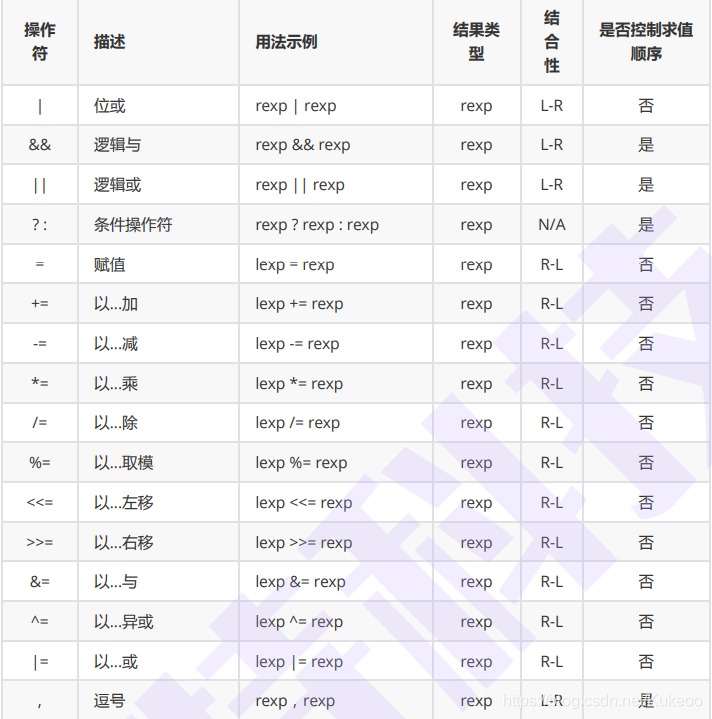
一些问题表达式（不要写出如下表达式）

//表达式的求值部分由操作符的优先级决定。
//表达式1
a*b + c*d +e*f

注释：代码1在计算的时候，由于*比+的优先级高，只能保证第一个*的计算是比第一个+早，但是优先级并不能决定第三个*比第一个+早执行。

所以表达式的计算机顺序就可能是：

a*b

c*d

a*b + c*d

e*f

a*b + c*d + e*f

或者

a*b

c*d

e*f

a*b + c*d

a*b + c*d + e*f

有歧义。（比如abc是表达式，会影响后面的值）

表达式2：

c + --c;

注释：

同上，操作符的优先级只能决定自减--的运算在+的运算的前面，但是我们并没有办法得知，+操作符的左操作数的获取在右操作数之前还是之后求值，所以结果是不可预测的，是有歧义的。

代码3-非法表达式

int main()
{
 int i = 10;
 i = i-- - --i * ( i = -3 ) * i++ + ++i;
 printf("i = %d\n", i);
 return 0;
}

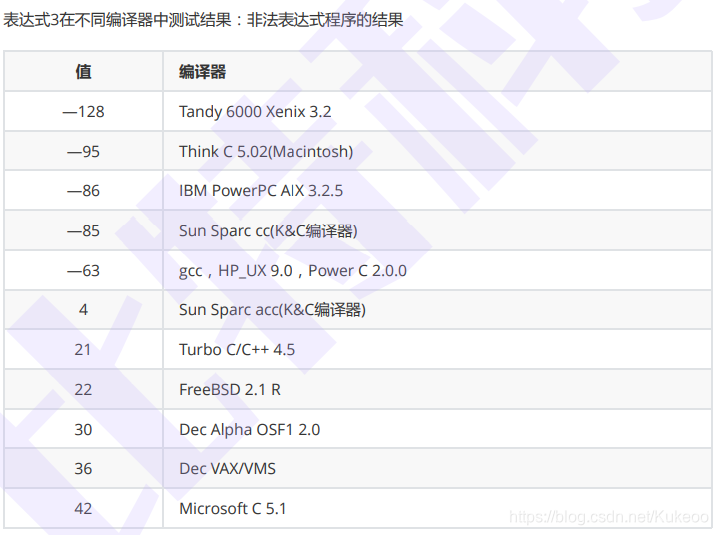
代码4

//代码4
int fun()
{
     static int count = 1;
     return ++count;
}
int main()
{
     int answer;
     answer = fun() - fun() * fun();
     printf( "%d\n", answer);//输出多少？
     return 0;
}

这个代码有没有实际的问题？

有问题！

虽然在大多数的编译器上求得结果都是相同的。

但是上述代码 answer = fun() - fun() * fun(); 中我们只能通过操作符的优先级得知：先算乘法，再算减法。

函数的调用先后顺序无法通过操作符的优先级确定。

函数会进行三次调用，依次返回3个值：2，3，4

但是第一个先调用还是第二个先调用呢？

可能有如下两种结果：

2-3×4

4-2×3

结果不同。

代码5

//代码5
#include <stdio.h>
int main()
{
 int i = 1;
 int ret = (++i) + (++i) + (++i);
 printf("%d\n", ret);
 printf("%d\n", i);
 return 0;
}
//尝试在linux 环境gcc编译器，VS2013环境下都执行，看结果

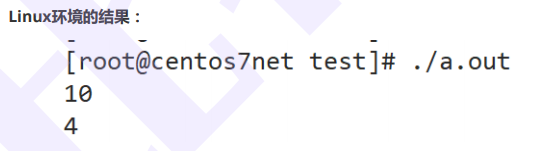
VS2013环境下的结果：

 

看看同样的代码产生了不同的结果，这是为什么？

简单看一下汇编代码.就可以分析清楚。

这段代码中的第一个 + 在执行的时候，第三个++是否执行，这个是不确定的，

因为依靠操作符的优先级和结合性是无法决定第一个 + 和第三个前置 ++ 的先后顺序。

 

总结：我们写出的表达式如果不能通过操作符的属性确定唯一的计算路径，那这个表达式就是存在问题的。