【轴承故障分解】ITD轴承故障信号分解【含Matlab源码 1871期】

💥💥💥💥💥💥💥💥💞💞💞💞💞💞💞💞💞Matlab武动乾坤博客之家💞💞💞💞💞💞💞💞💞💥💥💥💥💥💥💥💥
🚀🚀🚀🚀🚀🚀🚀🚀🚀🚀🚤🚤🚤🚤🚤🚤🚤🚤🚤🚤🚤🚤🚤🚤🚤🚤🚤🚤🚤🚤🚀🚀🚀🚀🚀🚀🚀🚀🚀🚀

🔊博主简介：985研究生，Matlab领域科研开发者；

🚅座右铭：行百里者，半于九十。

🏆代码获取方式：
优快云 Matlab武动乾坤—代码获取方式

更多Matlab信号处理仿真内容点击👇
①Matlab信号处理（进阶版）

⛳️关注优快云 Matlab武动乾坤，更多资源等你来！！

⛄一、ITD轴承故障信号分解简介

滚动轴承局部损伤故障振动信号多为非平稳的多分量调制信号, 采用合适的时频分析方法将故障信号分解为若干个单分量AM-FM信号, 再对其包络解调是轴承故障诊断的常用手段。本征时间尺度分解 (Intrinsic Time-Scale Decomposition, ITD) 是针对传统时频分析方法的局限性提出的新方法, 可自适应性地将一个复杂信号分解为若干个合理旋转 (Proper Rotation, PR) 分量之和, 每个PR分量通过一次迭代即可获得, 端点效应小, 分解能力强, 计算速度明显优于经验模态分解 (Empirical Mode Decomposition, EMD) 和局部均值分解 (Local Mean Decomposition, LMD) 方法, 有利于实现在线故障诊断。

1 ITD方法
1.1 原理
设待分解信号Xt的极值为Xk, 对应时刻为τk (k=1, 2, …, N, N为所有极值点个数) 。定义L为基线提取算子, Lt=LXt为信号的基线分量, 则Xt被分解为Xt=Lt+Ht, Ht为待提取的PR分量。
(1) L通过相邻基线控制点Lk和Lk+1在[τk, τk+1] (k=1, 2, …, N) 上对Xt线性变换所得, 即

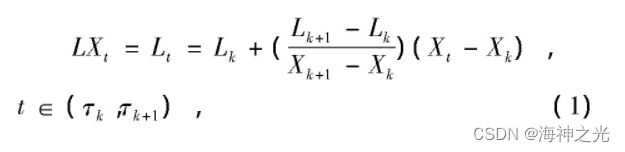
其中每个基线控制点为

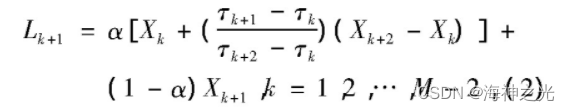
式中:α为线性增益, 一般取0.5。

(2) 定义一个固有旋转分量提取算子LXt, 则

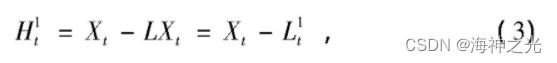
式中:Ht1为分离出来的最高频率的PR分量。然后将Lt1作为原始信号, 重复上述步骤, 直到基线信号Ltp为一单调或常函数, 原始信号被分解为

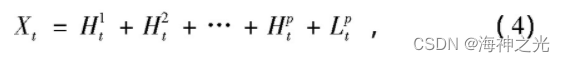
式中:Hti为第i个PR分量;Ltp为第p次分解后的残余分量。

ITD方法中的基线通过信号的线性变换得到, 避开了EMD方法中求极大值和极小值包络时使用的两次、三次样条拟合, 从而缩短计算时间, 减少拟合误差, 所以ITD方法端点效应小且计算速度快。

1.2 新迭代终止条件
由上述原理可知, ITD方法进行PR分量分解的迭代终止条件为基线信号Ltp为一单调或常函数。原始信号各分量的信息主要集中在前几个能量较高的PR分量中, 尤其当存在噪声成分时, 后几个PR分量为无意义的受干扰分量。为进一步减少计算量, 加快分解速度, 从能量角度出发提出ITD方法的新迭代终止条件。

⛄二、部分源代码

function [H,L]=Itd(x,n,err)
% 将信号x进行ITD分解
% n分解层数 自己设定的最大的分解层 若没有这么多次 也会自动停止
% err 为常函数的值小于这个值的时候停止
%--------------------------
if nargin1 %输入变量个数
n=3;
err=0.05;
end
if nargin2
err=0.05;
end
[tempH1,tempL]= Intrinsic_timescale_decomposition(x);
H=tempH1;
H=[];
for i=1:n
[tempH,tempL]= Intrinsic_timescale_decomposition(x);
H=[H;tempH]; %行矩阵
%----终止条件
%有两个终止条件 一个是基线信号为单调函数 一个是常函数
if dandiao(tempL)==1 %单调函数
break;
end
if max(tempL)<err && abs(min(tempL))<err %常函数 正负数的绝对值都要满足即绝对值在err之间
break;
end
x=tempL;
%-------
end
L=tempL;
end
function rlt=dandiao(xx)
% 求是否单调函数
x1=diff(xx);
rlt=0;
if all(x1>=0) || all(x1<=0)
rlt=1;
end
end

⛄三、运行结果

⛄四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1]唐贵基,庞彬.基于ITD和切片双谱的滚动轴承局部损伤故障诊断[J].轴承. 2014,(08)

3 备注
简介此部分摘自互联网，仅供参考，若侵权，联系删除

🍅 仿真咨询
1 各类智能优化算法改进及应用
生产调度、经济调度、装配线调度、充电优化、车间调度、发车优化、水库调度、三维装箱、物流选址、货位优化、公交排班优化、充电桩布局优化、车间布局优化、集装箱船配载优化、水泵组合优化、解医疗资源分配优化、设施布局优化、可视域基站和无人机选址优化

2 机器学习和深度学习方面
卷积神经网络（CNN）、LSTM、支持向量机（SVM）、最小二乘支持向量机（LSSVM）、极限学习机（ELM）、核极限学习机（KELM）、BP、RBF、宽度学习、DBN、RF、RBF、DELM、XGBOOST、TCN实现风电预测、光伏预测、电池寿命预测、辐射源识别、交通流预测、负荷预测、股价预测、PM2.5浓度预测、电池健康状态预测、水体光学参数反演、NLOS信号识别、地铁停车精准预测、变压器故障诊断

3 图像处理方面
图像识别、图像分割、图像检测、图像隐藏、图像配准、图像拼接、图像融合、图像增强、图像压缩感知

4 路径规划方面
旅行商问题（TSP）、车辆路径问题（VRP、MVRP、CVRP、VRPTW等）、无人机三维路径规划、无人机协同、无人机编队、机器人路径规划、栅格地图路径规划、多式联运运输问题、车辆协同无人机路径规划、天线线性阵列分布优化、车间布局优化

5 无人机应用方面
无人机路径规划、无人机控制、无人机编队、无人机协同、无人机任务分配

6 无线传感器定位及布局方面
传感器部署优化、通信协议优化、路由优化、目标定位优化、Dv-Hop定位优化、Leach协议优化、WSN覆盖优化、组播优化、RSSI定位优化

7 信号处理方面
信号识别、信号加密、信号去噪、信号增强、雷达信号处理、信号水印嵌入提取、肌电信号、脑电信号、信号配时优化

8 电力系统方面
微电网优化、无功优化、配电网重构、储能配置

9 元胞自动机方面
交通流 人群疏散 病毒扩散 晶体生长

10 雷达方面
卡尔曼滤波跟踪、航迹关联、航迹融合