1、聚类算法简介
聚类算法是一类无监督学习方法,旨在将数据划分为若干组(簇),使得同一簇内的样本相似度高,而不同簇间的样本差异大。计算样本之间相似度常用的方式是欧式距离;聚类算法的目的是在没有先验知识的情况下,自动发现数据集中的内在结构和模式。
常见聚类算法主要划分为:
- 基于划分的聚类:K-means算法->按照质心(一个簇的中心位置,通过均值计算)分类
- 基于层次的聚类:DIANA(自顶向下)AGNES(自底向上)
- 基于密度的聚类: DBSCAN算法
- 基于图的聚类: 谱聚类(Spectral Clustering)
2、K-Means
2.1、算法介绍
K-Means是一种常用的聚类算法,算法的步骤大致为:
- 事先确定常数K ,常数K意味着最终的聚类类别数
- 随机选择 K 个样本点作为初始聚类中心
- 计算每个样本到 K 个中心的距离,选择最近的聚类中心点作为标记类别
- 根据每个类别中的样本点,重新计算出新的聚类中心点(平均值),如果计算得出的新中心点与原中心点一样则停止聚类,否则重新进行第 3 步过程,直到聚类中心不再变化
K-Mean算法也可以说是一种EM(Expectation-Maximization)算法,它的问题描述为:
输入N个样本{xi}i=1∼N\{x_i\}_{i=1\sim N}{xi}i=1∼N,输出N个样本类别{Zi}i=1∼N\{Z_i\}_{i=1\sim N}{Zi}i=1∼N,其中Zi=1,2,3......K{Z_i = 1,2,3......K}Zi=1,2,3......K。
① 首先,随机化μ1,μ2,......μkμ_1,μ_2,......μ_kμ1,μ2,......μk
② E-Step:
Zi=argmink∣∣xi−μk∣∣(离谁近属于谁)Z_i = arg\underset {k}{min}||x_i-μ_k|| (离谁近属于谁)Zi=argkmin∣∣xi−μk∣∣(离谁近属于谁)
③ M-Step:
y={Nk=∑i=1NI(Zi=k)(N个样本中有多少个属于第k类)μk=1Ni∑i=1Nxi(μk是第k类样本的均值)(1)y=
\begin{cases}
N_k=\sum\limits_{i=1}^N I (Z_i=k)(N个样本中有多少个属于第k类)\\
μ_k=\frac{1}{N_i}\sum\limits_{i=1}^N x_i(μ_k是第k类样本的均值)\quad
\end{cases}
\tag{1}y=⎩⎨⎧Nk=i=1∑NI(Zi=k)(N个样本中有多少个属于第k类)μk=Ni1i=1∑Nxi(μk是第k类样本的均值)(1)
④ 回到 ②,直到收敛
优化目标:E=min∑i=1K∑x∈Cidist(Ci,x)2(Ci是簇中心)E = min\sum\limits_{i=1}^K \sum\limits_{x\in{C_i}}dist(C_i,x)^2(C_i是簇中心)E=mini=1∑Kx∈Ci∑dist(Ci,x)2(Ci是簇中心)
2.2、评估方法、K值选择
误差平方和SSE (The sum of squares due to error) :
SSE越小聚类效果越好;模型的inertia_ 属性即为SSE值。
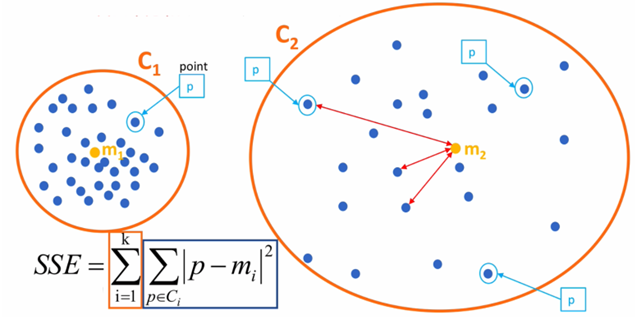
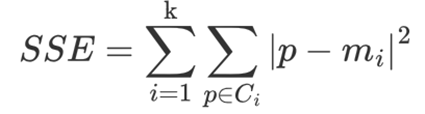
Ci表示簇C_i 表示簇Ci表示簇
k表示聚类中心的个数k 表示聚类中心的个数k表示聚类中心的个数
p表示某个簇内的样本p 表示某个簇内的样本p表示某个簇内的样本
m表示质心点m 表示质心点m表示质心点
“肘”方法 (Elbow method):
“肘” 方法通过 SSE 确定 n_clusters 的值,即确定K值。
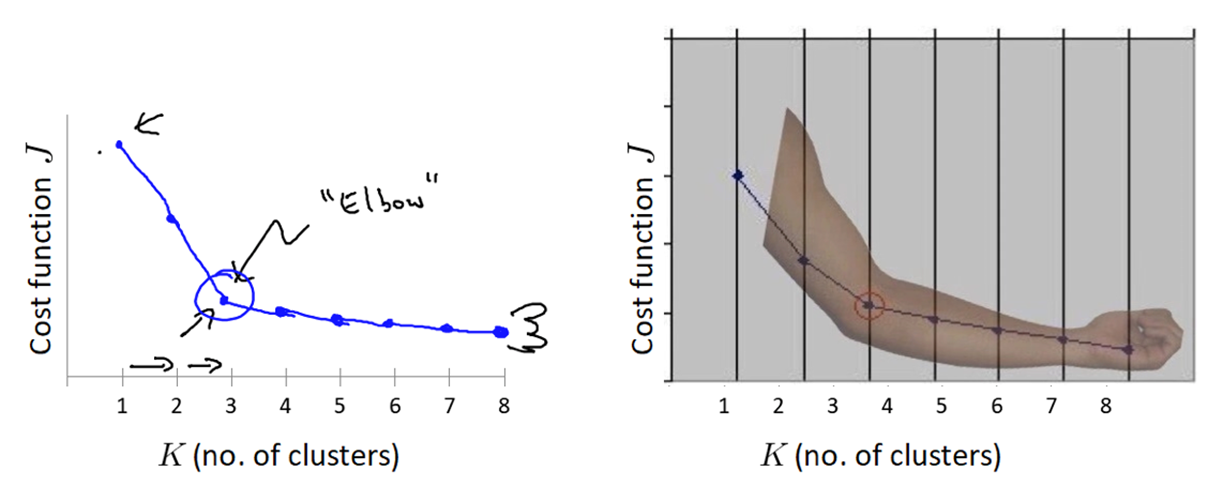
步骤
1、对于n个点的数据集,迭代计算 k from 1 to n,每次聚类完成后计算 SSE
2、SSE 是会逐渐变小的,因为每个点都是它所在的簇中心本身。
3、SSE 变化过程中会出现一个拐点,下降率突然变缓时即认为是最佳 n_clusters 值。
4、在决定什么时候停止训练时,肘形判据同样有效,数据通常有更多的噪音,在增加分类无法带来更多回报时,我们停止增加类别。
SC轮廓系数法(Silhouette Coefficient):
轮廓系数法考虑簇内的内聚程度(Cohesion),簇外的分离程度(Separation)
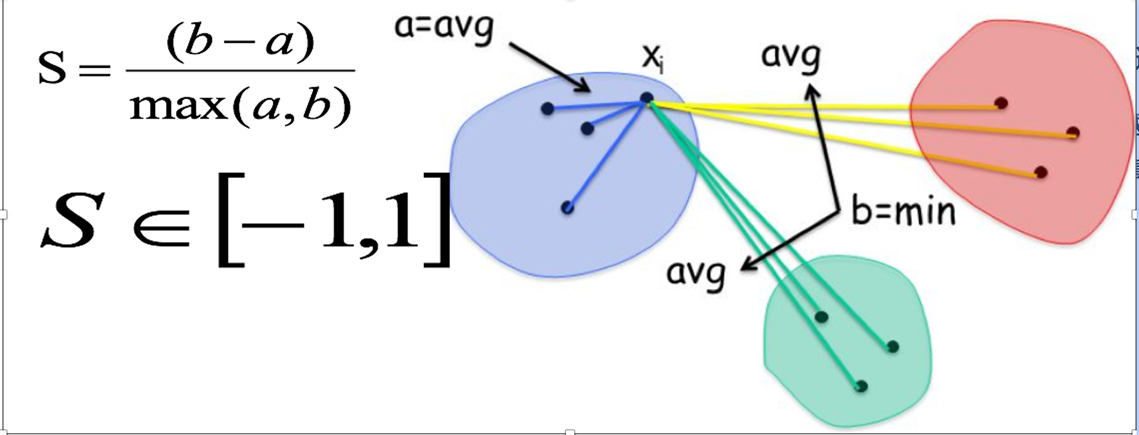
上图是轮廓系数计算方法;最后计算所有样本的平均轮廓系数,轮廓系数的范围为:[-1, 1],SC值越大聚类效果越好。
API:
from sklearn.metrics import silhouette_score()
CH轮廓系数法(Calinski-Harabasz Index):
CH 系数考虑簇内的内聚程度、簇外的离散程度、质心的个数。
类别内部数据的距离平方和越小越好,类别之间的距离平方和越大越好。聚类的种类数越少越好。
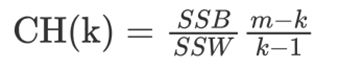
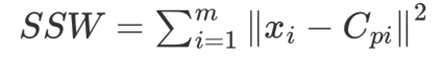


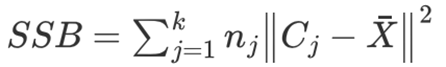


API:
from sklearn.metrics import calinski_harabasz_score ()
3、DBSCAN算法
DBSCAN 算法 (Density-Based Spatial Clustering of Applications with Noise)步骤:
① 核心对象 (Core Point)
若某个点的 r 邻域内点的数量不小于 MinPts,则该点为核心点。
② ε-邻域 (ε-neighborhood)
以点为中心、半径为 ε(算法设定的距离阈值)的区域。
③ 直接密度可达 (Directly Density-Reachable)
对于点 p 和 q:若
- p 在 q 的 ε 邻域内
- q 是核心点
则称 p 从 q 直接密度可达。
④ 密度可达 (Density-Reachable)
若存在一系列点 q₀, q₁, …, qₖ,使得对于任意 i(1 ≤ i ≤ k),点 qᵢ 从 qᵢ₋₁ 直接密度可达,则称 q₀ 到 qₖ 密度可达。这是直接密度可达的传播链。
⑤ 密度相连 (Density-Connected)
若存在核心点 p,使得点 q 和点 k 都是从 p 密度可达的,则称 q 和 k 是密度相连的。
⑥ 边界点 (Border Point)
属于某一个类簇的非核心点。它位于核心点的 ε 邻域内,但其自身邻域内点数不足 MinPts,因此“不能发展下线”。
⑦ 噪声点 (Noise Point)
不属于任何类簇的点。从任何核心点出发,该点都是密度不可达的。
参数选择建议
-
确定 MinPts 的参考值
- 对于二维数据集,通常取 MinPts = 4
- 更一般地,可取 MinPts ≥ 维度 + 1(至少为 3)
- 值越小,模型越敏感,易形成小簇;值越大,对噪声越鲁棒,但可能忽略小簇
-
确定 ε (半径) 的经验方法
- 计算数据集中每个点到其第 k 个最近邻的距离(k 距离),k 一般取 MinPts
- 将所有点的 k 距离按从小到大排序,绘制 k 距离曲线
- 在曲线中找到拐点(“肘部”)对应的距离值,作为 ε 的参考值
- 一般 ε 取小一些,并通过多次实验调整
-
调参流程建议
- 先固定 MinPts(如 4),尝试不同 ε
- 观察聚类结果,若大部分点被标记为噪声,则 ε 可能过小;若所有点聚成一类,则 ε 可能过大
- 结合 k 距离曲线和实际业务需求综合确定
算法特点总结
| 特点 | 说明 |
|---|---|
| 无需指定簇数 | 自动发现任意形状的簇 |
| 抗噪声能力强 | 可识别并排除噪声点 |
| 对参数敏感 | ε 和 MinPts 需仔细调优 |
| 处理密度不均 | 对密度差异大的数据集效果可能不佳 |
代码示例
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt
from sklearn.metrics import silhouette_score, calinski_harabasz_score
data = make_blobs(n_samples=1000, n_features=2, centers=[[1,1],[3,2],[5,3],[7,6]],
cluster_std=[1, 0.5, 1.5, 1.2], random_state=6)
x = data[0]
y = data[1]
k_list = [i for i in range(2,11)]
sse_list = []
sc_list = []
ch_list = []
for k in k_list:
model = KMeans(n_clusters=k)
y_pred = model.fit_predict(x)
sse_list.append(model.inertia_)
sc_list.append(silhouette_score(x, y_pred))
ch_list.append(calinski_harabasz_score(x, y_pred))
fig = plt.figure(figsize=(10,10), dpi=60)
fig.add_subplot(311)
plt.plot(k_list, sse_list)
plt.title("SSE")
fig.add_subplot(312)
plt.plot(k_list, sc_list)
plt.title("sc")
fig.add_subplot(313)
plt.plot(k_list, ch_list)
plt.title("ch")
plt.show()




















 10万+
10万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








