刷题day50：N皇后

题意描述：

按照国际象棋的规则，皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。

n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

给你一个整数 n ，返回所有不同的 n 皇后问题 的解决方案。

每一种解法包含一个不同的 n 皇后问题 的棋子放置方案，该方案中 'Q' 和 '.' 分别代表了皇后和空位。

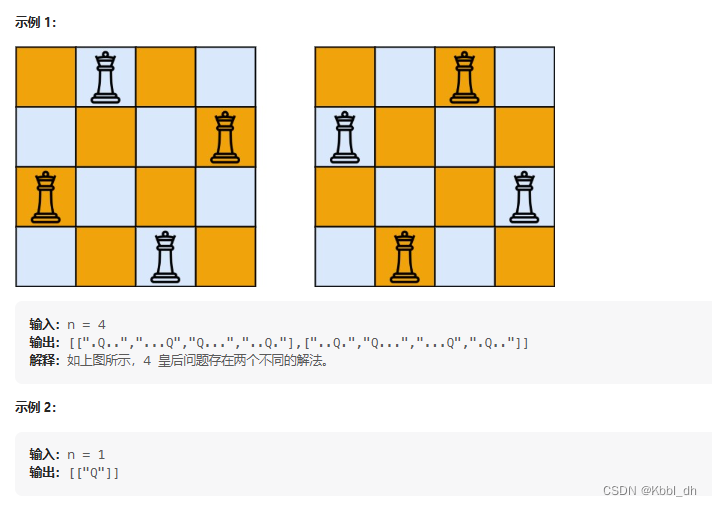
 主要思路把皇后不能互相攻击的路径找到就可以，不能在一条横线上，不能在一条竖线上，不能在斜线上，其中斜线分为45°和135°两种。

完整C++代码如下：

class Solution {
private:
    vector<vector<string>> result;
    bool isValid(int row, int col, vector<string>& chessboard, int n){
        for(int i = 0; i < row; i++){
            if(chessboard[i][col] == 'Q'){
                return false;
            }
        }
        for(int i = row - 1, j = col - 1; i >= 0 && j >= 0; i--, j--){
            if(chessboard[i][j] == 'Q'){
                return false;
            }
        }
        for(int i = row - 1, j = col + 1; i >= 0 && j < n; i--, j++){
            if(chessboard[i][j] == 'Q'){
                return false;
            }
        }   
        return true;
    }
    void backtracking(int n, int row, vector<string>& chessboard){
        if(row == n){
            result.emplace_back(chessboard);
            return;
        }
        for(int col = 0; col < n; col++){
            if(isValid(row, col, chessboard, n)){
                chessboard[row][col] = 'Q';
                backtracking(n, row + 1, chessboard);
                chessboard[row][col] = '.';
            }
        }
    }
public:
    vector<vector<string>> solveNQueens(int n) {
        result.clear();
        std::vector<std::string> chessboard(n, std::string(n, '.'));
        backtracking(n, 0, chessboard);
        return result;
    }
};