本文详细介绍了二叉树的概念，包括树的结构、二叉树的存储方式，重点讲解了二叉树的遍历方法，如深度优先遍历（前序、中序、后序）和广度优先遍历。此外，还探讨了二叉搜索树（BST）相对于哈希表的优势，并提供了相关题目进行实战练习。
【待更新】
6. 树
6.1 树的结构
Terminology of Tree
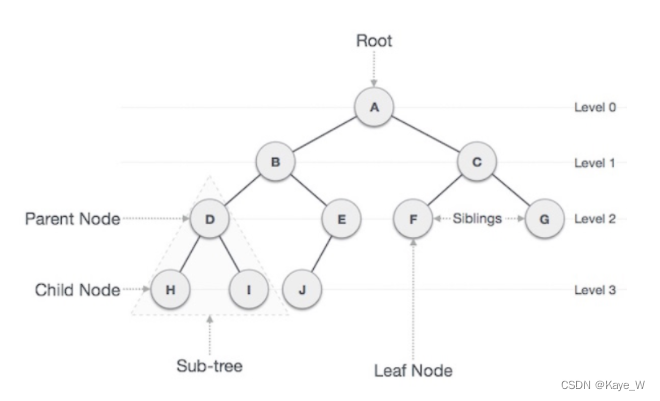
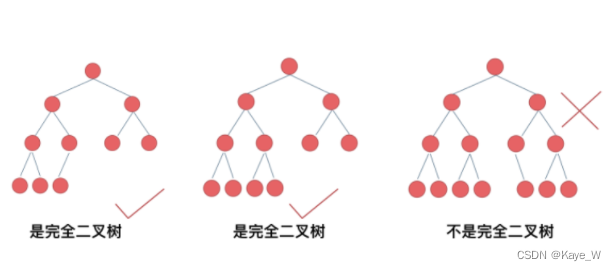
Complete binary search tree完全二叉树
Binary Search Tree
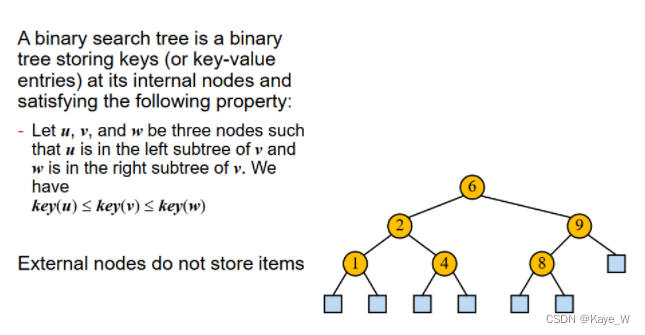
满二叉树、完全二叉树无数值，从BST开始，internal nodes(非leaf node)包含数值。这里注意，node和左右节点的值可能相同。
AVL Tree
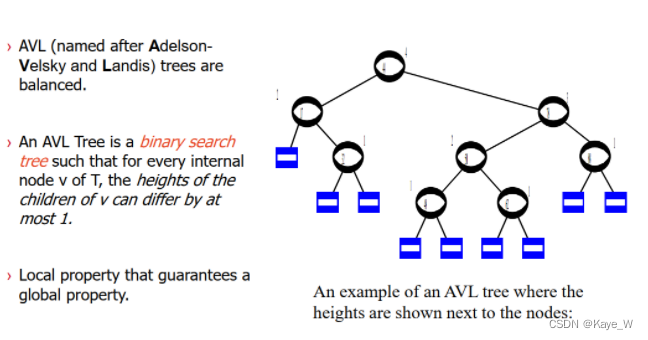
6.2 二叉树的储存方式
- 顺序储存 -> 按照parent -> left child -> right child -> left grandchild of left child -> right gradchild of left child… 的顺序储存在连续内存中 -> 以数组作为容器。
- 链式储存，每个node同时包含两指针，分别指向left child和right child，更常用。
6.3 二叉树的遍历方法
- 深度优先遍历
- 前序遍历（递归法，迭代法）
- 中序遍历（递归法，迭代法）
- 后序遍历（递归法，迭代法）
- 广度优先遍历
- 层次遍历（迭代法）
前中后序遍历的区别在于：中间节点的位置。
前序遍历（中左右）：{10, 5, 1, 7, 40, 50}
中序遍历（左中右）：{1, 5, 7, 10, 40, 50}
后序遍历（左右中）：{1, 7, 5, 50, 40, 10}
10
/ \
5 40
/ \ \
1 7 50
6.4 Advantages of BST over HashTable
HashTable 在search, insert, delete操作中都能达到O(1)，然而自平衡树BST(avl tree, res black tree等)需要O(logn). 除了Time Complexity之外，BST与HashTable的优越性体现在哪些情况下呢？
- BST中，中序遍历可以得到sorted结果in O(logn)，在HashTable中不是natural operation需要extra effort.
- Doing order statistics, finding closest lower and greater elements, doing range queries are easy to do with BSTs
- BSTs are easy to implement compared to hashing. Libraries are needed when implementing hasing.
- With Self-Balancing BSTs, all operations are guaranteed to work in O(Logn) time. But with Hashing, Θ(1) is average time and some particular operations may be costly i.e, O(n2 ), especially when table resizing happens.
6.5 二叉树相关题目
6.5.1 Define a TreeNode 树节点的定义
class TreeNode{
int val;
TreeNode left;
TreeNode right;
TreeNode(){}
TreeNode(int val){this.val = val;}
TreeNode(int val, TreeNode left, TreeNode right){
this.val = val;
this.left = left;
this.rihgt = right;
}
}
6.5.2 BST Traversal 二叉树遍历
虽然以下分类是按照递归、迭代和层序遍历，但层序遍历是和前中后序遍历同级别，对遍历输出结果的要求；而递归和迭代是代码思路和书写方式，可分别应用于前中后及层序遍历。
6.5.2.1 Recursive Traserval 递归遍历
递归法 recursive, O(n), 节点个数
class Solution {
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
preOrder(res, root);
return res;
}
void preOrder(List<Integer> res, TreeNode root){
if (root == null) return;
res.add(root.val);
preOrder(res, root.left);
preOrder(res, root.right);
}
}
后序遍历类似，中序遍历在6.5.3，不多赘述。
6.5.2.2 Iterative Traserval 用栈迭代
递归那么简单，为什么要学其他方法？在实际项目开发的过程中我们是要尽量避免递归！因为项目代码参数、调用关系都比较复杂，不容易控制递归深度，甚至会栈溢出。
前序遍历
用栈实现：出栈顺序：中左右，入栈顺序中右左。
具体地，中 -> 出栈 -> 右入栈 -> 左入栈 -> 左出栈 -> 右出栈
class Solution{
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
if (root == null) return res;
Stack<TreeNode> stack = new Stack<>();
stack.push(root);
while (!.stack.isEmpty()){
TreeNode node = stack.pop();
res.append(node.val);
if (node.right != null)
stack.push(node.right);
if (node.left != null)
stack.push(node.left);
}
return res;
}
}
中序遍历
preorder先处理的是根节点，但inorder要先处理最左边，直到左边为null，访问和处理位置不一致，因此使用cur代表访问位置。
class Solution{
public List<Integer> inorderTraversal(TreeNode){
List<Integer> res = new ArrayList<>();
if (root == null) return res;
Stack<TreeNode> stack = new Stack<>();
TreeNode cur = root;
while (cur!= null || !stack.isEmpty()){
if (cur != null){
stack.push(cur);
cur = cur.left;
}else{
cur = stack.pop();
res.add(cur.val);
cur = cur.right;
}
}
return res;
}
}
后序遍历
输出顺序 左右中， 如果颠倒过来的话就是中右左，和前序遍历一样。
把入栈顺序改成中左右，以中右左顺序出栈，再将结果翻转，得到后序遍历结果。
class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
if (root ==null) return res;
Stack<TreeNode> stack = new Stack<>();
stack.push(root);
while (!stack.isEmpty()){
TreeNode node = stack.pop();
res.add(node.val);
if (node.left != null) stack.push(node.left);
if (node.right != null) stack.push(node.right);
}
Collections.reverse(res);
return res;
}
}
6.5.2.3 层序遍历 levelorder
需要借用一个辅助数据结构即队列来实现，队列先进先出，符合一层一层遍历的逻辑，而是用栈先进后出适合模拟深度优先遍历也就是递归的逻辑。而这种层序遍历方式就是图论中的广度优先遍历，只不过我们应用在二叉树上。
方法一：recursion递归, DFS
方法二：iteration迭代，BFS
class Solution {
List<List<Integer>> res = new ArrayList<List<Integer>>();
public List<List<Integer>> levelOrder(TreeNode root) {
checkFun01(root, 0);
return res;
}
/* Method1, recursion, DFS
*/
public void checkFun01(TreeNode root, Integer deep){
if (root == null) return;
deep++;
if (res.size() < deep){
// initialise item list in current level
List<Integer> item = new ArrayList<>();
res.add(item);
}
// 注意这里deep - 1 means 当前deep-1
res.get(deep-1).add(root.val);
checkFun01(root.left, deep);
checkFun01(root.right, deep);
}
/* Method2, using queue, BFS
*/
public void checkFun02(TreeNode root){
if (root == null) return;
Queue<TreeNode> q = new LinkedList<TreeNode>();
q.offer(root);
while (!q.isEmpty()){
List<Integer> items = new ArrayList<>();
int len = q.size();
while (len > 0){
TreeNode node = q.poll();
items.add(node.val);
if (node.left != null) q.offer(node.left);
if (node.right != null) q.offer(node.right);
// 千万别忘记更新参数，不然add null报错
len--;
}
res.add(items);
}
}
}
同类型的题目：
剑指 Offer 32 - I. 从上到下打印二叉树
剑指 Offer 32 - III. 从上到下打印二叉树 III
107. 二叉树的层序遍历 II
515. 在每个树行中找最大值
6.5.3 Search and Insertion 搜索和插入
在BST中插入节点之前，首先判断root node是否存在，若不存在则需要创建一棵树。
其次，需要找到合适的插入位置。
伪代码：
if root is null
then create root node
return
if root exists then
compare the data with node.data
while until the insertion position is located
if data is greater then node.data
goto right subtree
else
goto left subtree
endwhile
insert data
end if
Code
class BST{
// class that defines tree nodes
class Node{
int val;
Node left;
Node right;
Node(){}
Node(int val){this.val = val;}
Node(int val, Node left, Node right){
this.val = val;
this.left = left;
this.rihgt = right;
}
}
Node root;
// constructors
// initialisation with an empty tree
BST(){
this.root = null;
}
BST(int val){
this.root = new Node(val);
}
// operations
// search a node in BST
Node search(Node root, int value){
if (root == null || root.val = value){
return root;
}
// 如果val大于根节点的之，在右子树继续找
if (value > root.val){
return search(root.right, val);
}
// 反之，在左子树继续找
return search(root.left, val);
}
/*
因为要进行recursive traversal的过程
就像建立dummyhead和遍历移动的cur指针一样
建立住function和utility function来递归遍历
*/
// This method mainly calls insertRec()
void insert(int val){
root = insertRec(root, val);
}
/* A recursive function to
insert a new key in BST */
Node insertRec(Node root, int val){
if (root == null){
root = new Node(val);
return root;
}
if (val > root.val){
// 这里千万注意，是改变了子树
// 不能call the utility function without assigning it
root.right = insertRec(root.right, val);
}else{
//相同值放在了做左边节点
root.left = insertRec(root.left, val);
}
/*
return the unchanged node pointer
这里需要注意， 由于recursivly改变了左右节点直到insertion location
最终node pointer返回的是根节点
*/
return root;
}
// This function mainly calls the InorderRec
void inorder(Node root){
return inorderRec(root);
}
// The utility function traversing revursivly
void inorderRec(Node root){
if (root != null){
inorderRec(root.left);
System.out.println(root.val);
inorderRec(root.right);
}
}
}
对于Search和Insertion，Time Complexity: O(log(n)) where log(n) is the height of the tree. 对于skewed tree来说，它的高度是n因此in the worst case it takes O(n).
6.5.4 Delete 删除
class BST{
// Node defination
Node root;
// constructors
// This method mainly calls the deleteRec function
void delete(int val){
deleteRec(root, val);
}
// utility function
Node deleteRec(Node root, int val){
// base case: if the tree is empty
if (root == null){
return root;
}
// otherwise, recur down the tree
if (val > root.val){
root.right = deleteRec(root.right, val);
}else if(val < root.val){
root.left = deleteRec(root.left, val);
}
// val == root.val, delete root
else{
// root with only one child or no child
if (root.left == null)
return root.right;
else if (root.right == null)
return root.left;
// node with teo children
// get the inorder successor
// find the smallest one in the right subtree
// 只是更改了root.val
root.val = minValue(root.right);
// delete the successor
root.right = deleteRec(root.right, root.val);
}
return root;
}
Node minValue(Node root){
int minval = root.val;
while (root.left != null){
minval = root.left.val;
root = root.left;
}
return minval;
}
}
6.5.6 Conversion 二叉树的翻转
// DFS
class Solution {
public TreeNode invertTree(TreeNode root) {
if (root == null) return root;
invertTree(root.left);
invertTree(root.right);
swapChildren(root);
return root;
}
void swapChildren(TreeNode root){
TreeNode node = root.left;
root.left = root.right;
root.right = node;
}
}
现在感觉到，DFS就是要考虑最底层节点的情况。
//BFS
class Solution {
public TreeNode invertTree(TreeNode root) {
if (root == null) return root;
ArrayDeque<TreeNode> q = new ArrayDeque<>();
q.offer(root);
while (!q.isEmpty()){
int size = q.size();
while (size-- > 0){
TreeNode node = q.poll();
swap(node);
if (node.left != null) q.offer(node.left);
if (node.right != null) q.offer(node.right);
}
}
return root;
}
void swap(TreeNode node){
TreeNode tmp = node.left;
node.left = node.right;
node.right = tmp;
}
}
// ArrayDeque<TreeNode> q = new ArrayDeque<>();
// 比Queue<TreeNode> q = new LinkedList<>();
// 占用内存少
BFS时，首先从上到下逐层对节点进行操作。BFS首先考虑清楚辅助数据类型用栈还是队列，用队列的话每层记得用size作为判断循环的条件。
6.4.6 对称二叉树
想到的第一方法是，层序遍历，每层检查是否对称。
但下图这种情况无法解决，不是镜像对称。
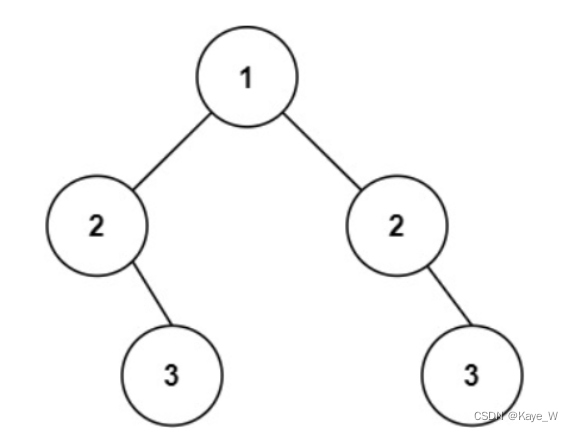
思路：左边前序遍历，中左右。
右边镜像，应为：中右左 ->左右中的翻转。
因此，右边后序遍历，再翻转结果。
然后判断左右两棵树遍历得到的结果是否相同即可。
6.4.7 [Construct BST from preorder]
Reference:
https://www.geeksforgeeks.org/binary-search-tree-set-1-search-and-insertion/
https://www.softwaretestinghelp.com/binary-search-tree-in-java/#Binary_Search_Tree_BST_Implementation_In_Java
https://programmercarl.com/%E4%BA%8C%E5%8F%89%E6%A0%91%E7%9A%84%E8%BF%AD%E4%BB%A3%E9%81%8D%E5%8E%86.html#%E5%89%8D%E5%BA%8F%E9%81%8D%E5%8E%86-%E8%BF%AD%E4%BB%A3%E6%B3%95
扫一扫
875
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
