哈希表（散列表）必备基础知识

最近在读HashTable的源码，回过头来复习自己在大一上数据结构课程写的这篇哈希表，重构的毛病又犯了

借此机会，重构一下这篇博客，在文字描述上，让大家能更容易得接受哈希表的知识

另外，本篇博客还带着一篇关于哈希表基本操作的代码，用C++实现的

哈希C++)

WHAT IS HASH TABLE

哈希表是一种存储结构，你可以先它当成数组。

它并非适用于任何情况，哈希表主要适用于记录的关键字（key）与存储地址存在某种函数关系的数据，就像我们常用的键值对存储结构

哈希设计出来的核心就是加快查找速度，任何查找都能实现时间复杂度为O（1）

为了保证插入和查找的平均复杂度为 O(1)，hash table 底层一般都是使用数组来实现。对于给定的 key，一般先进行 hash 操作，然后相对哈希表的长度取模，将 key 映射到指定的位置

在Java中，这个哈希操作就是.hashcode（）

“相对哈希表的长度取模”，这个过程称需要走哈希函数

取模运算：

index = hash(key) % hash_table_size  // index 就是 key 存储位置的索引
    //hash(key) % hash_table_size 这个函数称哈希函数

哈希冲突：

哈希冲突也称哈希碰撞

关键字（key）不同而通过哈希函数计算出来的哈希函数值（地址）相同称哈希冲突，哈希冲突很难避免，哈希表设计的核心就是较好解决哈希冲突

例子：
假设hash表的大小为9（即有9个槽），现在要把一串数据存到表里：5,28,19,15,20,33,12,17,10
简单计算一下：

hash(5)=5, 所以数据5应该放在hash表的第5个槽里；

hash(28)=1，所以数据28应该放在hash表的第1个槽里；

hash(19)=1，也就是说，数据19也应该放在hash表的第1个槽里——于是就造成了碰撞（也称为冲突，collision）

哈希表产生冲突跟以下因素有关

• 哈希函数的设计不够漂亮
• 解决方案不够漂亮：由于哈希冲突不可避免，所以解决方案的有效性能决定哈希冲突的频率
• 装填因子不合理

装填因子

装填因子α=存储的记录个数/哈希表的大小，装填因子越小，冲突的可能性越小，通常使装填因子控制在0.6~0.9的范围内

java的hashmap 装填因子为0.75

哈希函数设计

直接定址法

以关键字key本身或关键字加上某个数值常量c作为哈希地址

直接定址法的哈希函数h(k)为：

hash(k) = k+c（k为关键字，c为常量）

例如，

hash(学号) = 学号-201001001

除留余数法

这个就是我们一开始说的取模法

把n个记录按key关键字映射到0～m-1的哈希空间中

除留余数法的哈希函数f(k)为：

f( key ) = key mod p ( p ≤ m )

模p=素数时出现冲突的可能性更小。

数字分析法

这个拿我当时上课看的PPT可以解释

比如Key（学号）= 2020423

Hash（key）=取key的末两位

即

Hash（2020423）=23

那么就选取23作为数组下标，存入2020423

在Java中，采用扰动函数法设计哈希函数

哈希冲突的解决方法

开放定址法

即冲突时找一个新的空闲的哈希地址，但这个地址是随机的

例如：

你买了电影票，到电影院时已经开映了，你的位置被别人占用了，你需要找一个空位置。这就是开放定址法的思路

线性探查法：

即冲突时找一个新的空闲的哈希地址，且这个新地址与冲突位置具有线性规律

线性探查法的数学递推描述公式为：

d[0]=h(k)

di=(d[i-1]+1) mod m (1≤i≤m-1)

模m是为了保证找到的位置在0～m-1（即哈希表空间大小）的有效空间中

这个方法会产生堆积聚集现象

看下图就明白了

平方探查法

思路：在电影院中找被占用位置的前后空位置！

平方探查法的数学描述公式为：

d[0]=h(k)

d[i]=(d[0]±i方) mod m (1≤i≤m-1)

查找的位置依次为：d[0]、 d[0 +1]、 d[0 -1] 、 d[0 +4]、 d[0 -4]

平方探查法是一种较好的处理冲突的方法，可以避免出现堆积现象。它的缺点是不能探查到哈希表上的所有单元，但至少能探查到一半单元

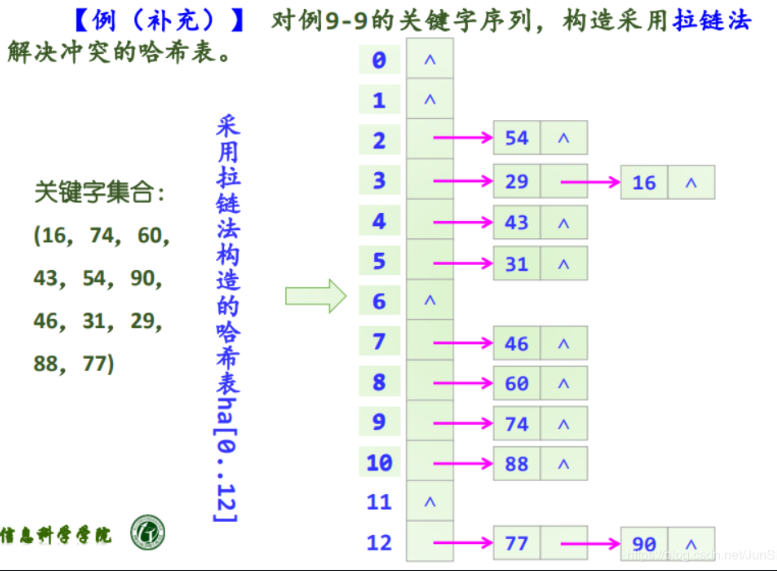
拉链法

这个方法也是最为常用的方法

存在哈希冲突的记录不用另寻空间，在冲突的位置设计有一个后继指针空间，放入即可

如下图

哈希查找

看到这， 其实出现冲突情况时的哈希查找算法已经说过了，就是上面的线性探查与平方探查

哈希查找算法的性能指标ASL

每个Key探查次数的累加/总记录数

ASL能帮助我们衡量哈希查找的“成功率”