A tree is an undirected connected graph without cycles.
Let's consider a rooted undirected tree with n vertices, numbered 1 through n. There are many ways to represent such a tree. One way is to create an array with n integers p1, p2, ..., pn, where pi denotes a parent of vertex i (here, for convenience a root is considered its own parent).
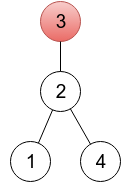 For this rooted
tree the array p is [2, 3, 3, 2].
For this rooted
tree the array p is [2, 3, 3, 2].Given a sequence p1, p2, ..., pn, one is able to restore a tree:
- There must be exactly one index r that pr = r. A vertex r is a root of the tree.
- For all other n - 1 vertices i, there is an edge between vertex i and vertex pi.
A sequence p1, p2, ..., pn is called valid if the described procedure generates some (any) rooted tree. For example, for n = 3 sequences (1,2,2), (2,3,1)and (2,1,3) are not valid.
You are given a sequence a1, a2, ..., an, not necessarily valid. Your task is to change the minimum number of elements, in order to get a valid sequence. Print the minimum number of changes and an example of a valid sequence after that number of changes. If there are many valid sequences achievable in the minimum number of changes, print any of them.
The first line of the input contains an integer n (2 ≤ n ≤ 200 000) — the number of vertices in the tree.
The second line contains n integers a1, a2, ..., an (1 ≤ ai ≤ n).
In the first line print the minimum number of elements to change, in order to get a valid sequence.
In the second line, print any valid sequence possible to get from (a1, a2, ..., an) in the minimum number of changes. If there are many such sequences, any of them will be accepted.
4 2 3 3 4
1 2 3 4 4
5 3 2 2 5 3
0 3 2 2 5 3
8 2 3 5 4 1 6 6 7
2 2 3 7 8 1 6 6 7
In the first sample, it's enough to change one element. In the provided output, a sequence represents a tree rooted in a vertex 4 (because p4 = 4), which you can see on the left drawing below. One of other correct solutions would be a sequence 2 3 3 2, representing a tree rooted in vertex 3 (right drawing below). On both drawings, roots are painted red.

In the second sample, the given sequence is already valid.
题意:给你一堆点阿,线阿,环阿,让你改最小的边(指向)变成树。
思路:有环拆环指向根节点,无环直接指向根节点。除非全是环否则根节点绝对不为环中的点(否则多变 一个点),用并查集查环,没有构成环添加,构成环变指向。
问题:夹克聚聚说他的dfs盖了139ms的时间戳,弱弱写的超时了...
代码:
#include <iostream>
#include <cstring>
#include <string>
#include <cstdio>
#include <algorithm>
using namespace std;
int father[200000 + 5];
int a[200000 + 5];
bool vis[200000 + 5];
int root = -1 ,sum;
int ffather(int x)
{
return father[x] == x?x:father[x]=ffather(father[x]);
}
void un(int x, int y) //合并:0-0-0-0 和 1-1-1-1,找到最边上的0,1,变成0-0-0-0==1-1-1-1
{
x = ffather(x);
y = ffather(y);
if(x == y)
return;
else
father[x] = y;
}
int main()
{
int n;
cin>>n;
for(int i = 1; i <= n; i++)
cin>>a[i];
for(int i = 1; i <= n; i++)
{
father[i] = i; //初始化
}
for(int i = 1; i <= n; i++)
{
if(a[i] == i)
{
root = a[i]; //找根节点
break;
}
}
for(int i = 1; i <= n; i++)
{
if(ffather(a[i]) == ffather(i)) //若加入i和a[i]则成环
{
if(root == -1) //给的数据全是环
{
root = i;
a[i] = i;
sum++;
}
else if(a[i] != root)
{
a[i] = root;
sum++;
}
}
else
un(i,a[i]);
}
for(int i = 1; i <= n; i++)
{
if(i == a[i] && i != root)
{
a[i] = root;
sum++;
}
}
cout<<sum<<endl<<a[1];
for(int i = 2; i <= n; i++)
cout<<" "<<a[i];
}





 给定一个可能不合法的树序列,你需要找到需要改变的最小元素数量以使其成为一个合法的树序列。合法序列必须有一个节点是自己的父节点,即根节点。输出需要更改的最小数量,并给出一个示例的合法序列。
给定一个可能不合法的树序列,你需要找到需要改变的最小元素数量以使其成为一个合法的树序列。合法序列必须有一个节点是自己的父节点,即根节点。输出需要更改的最小数量,并给出一个示例的合法序列。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








