【人工智能学习之高数篇】

1. Python-Math 模块

1.1 Math模块函数

math 模块提供了浮点数的数学运算函数，返回值均为浮点数。
print(dir(math))所有函数：

['acos', 'acosh', 'asin', 'asinh', 'atan',
'atan2', 'atanh', 'ceil', 'comb', 'copysign',
'cos', 'cosh', 'degrees', 'dist', 'e', 'erf',
'erfc', 'exp', 'expm1', 'fabs', 'factorial',
'floor', 'fmod', 'frexp', 'fsum', 'gcd', 'gamma',
'hypot', 'inf', 'isclose', 'isfinite', 'isinf',
'isnan', 'isqrt', 'lcm', 'ldexp', 'lgamma', 'log',
'log10', 'log1p', 'log2', 'modf', 'nan',
'nextafter', 'perm', 'pi', 'pow', 'prod',
'radians', 'remainder', 'sin', 'sinh', 'sqrt',
'tan', 'tanh', 'tau', 'trunc', 'ulp']

1.2 Python内置数学函数

print(abs(-100))
print(divmod(5, 2))
print(max(1, 2, 3))
print(min(1, 2, 3))
print(pow(2, 3))
print(round(1.5555, 2))
print(sum((1, 2, 3, 4)))

2.初等函数

初等函数是数学中一类基本的、常见的函数，它们通常可以用有限次的基本数学运算（比如加法、减法、乘法、除法、开方、指数、对数等）来表示。这些函数在数学和科学中起到非常重要的作用，因为它们能够描述和解释各种现实世界中的现象和关系。

简而言之: 初等函数就是由基本初等函数构成的复合函数。

初等函数:

• 值域（Y轴）: 值域就是因变量的取值范围
  它表示函数的结果或输出值，取决于自变量的值。
• 定义域（X轴）: 定义域就是自变量的取值范围
• 饱和性（是否是饱和函数）: 饱和之意即为当自变量无穷大时
  自变量的变化很难引起函数值的变化
• 变化趋势（函数曲线）: 函数在自变量变化的情况下，有没有确定的变化
• 单调性、周期性、奇偶性、连续性
• 奇函数：
  一个函数f(x)被称为奇函数，如果对于所有实数x，都满足 f(-x) = -f(x)。
  奇函数的图像通常对称于原点 (0, 0)，具有中心对称性。
  例如: f(-x) = x
• 偶函数：
  一个函数f(x)被称为偶函数，如果对于所有实数x，都满足 f(-x) = f(x)。
  偶函数的图像通常对称于y轴，具有轴对称性例如: f(x) = x^2

2.1 幂函数和指数函数的区别

• 幂函数（power）：y = x ** a
• 指数函数（exponential）：y = a ** x
• 对数函数（Logarithm）：y = log(a)X
  x为自变量，y为因变量，a为常数

import math
import numpy as np
from matplotlib import pyplot as plt
x = np.arange(-10, 10, 0.01)
y1 = x ** 2
y2 = np.power(x, 3)
y3 = pow(x, 4)
y4 = math.pow(2, 3)
plt.plot(x, y1), plt.plot(x, y2), plt.plot(x, y3),
plt.plot(x, y4)
# x and y must have same first dimension, but have
shapes (2000,) and (1,)
# plt.plot(x, y4)
print(f"{y4}")
plt.show()

• 三角函数：sin、cos、tan、cot、sec、csc

 import matplotlib.pyplot as plt
import numpy as np
x = np.arange(-10, 10, 0.1)
# 正弦函数
y1 = np.sin(x)
# 余弦函数
y2 = np.cos(x)
# 正切函数
y3 = np.tan(x)
# wspace=0.5 表示子图之间的水平间距为0.5个单位，这意味着相邻的子图在水平方向上会有一些空白间隙
# hspace 参数是指垂直方向的间距。在这里，hspace=1 表示子图之间的垂直间距为1个单位，
# 这意味着相邻的子图在垂直方向上会有更大的间距
grid = plt.GridSpec(2, 2, wspace=0.5, hspace=1)
plt.subplot(grid[0:1])
plt.plot(x, y1)
plt.subplot(grid[1:2])
plt.plot(x, y2)
plt.subplot(grid[2:4])
plt.plot(x, y3)
plt.xlabel('x', fontsize=12)
plt.show()

-反三角函数：arcsin、arccos、arctan

import matplotlib.pyplot as plt
import numpy as np
x = np.arange(-1, 1, 0.01)
y1 = np.arcsin(x) # 反正弦函数
y2 = np.arccos(x) # 反余弦函数
y3 = np.arctan(x) # 反正切函数
plt.plot(x, y1)
# plt.plot(x, y2)
# plt.plot(x, y3)
plt.show()

• 阶跃函数
  一种特殊的连续时间函数，是一个从0跳变到1的过程，属于奇异函数。

3.复合函数

复合函数由两个初等函数复合而成，将其中一个初等函数(次级函数)镶嵌在另外一个初等函数(主体函数)中。

4.激活函数

在神经网络中，输入经过权值加权计算并求和之后，需要经过一个函数的作用，这个函数就是激活函数（ActivationFunction）。激活函数是一种复合函数。

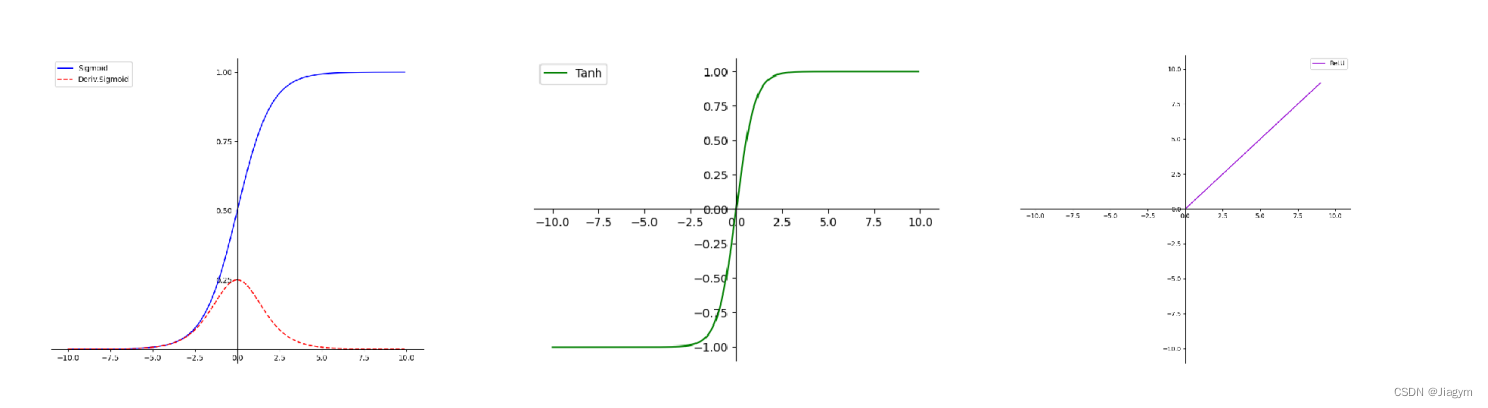
4.1激活函数：Sigmoid（S型生长曲线）

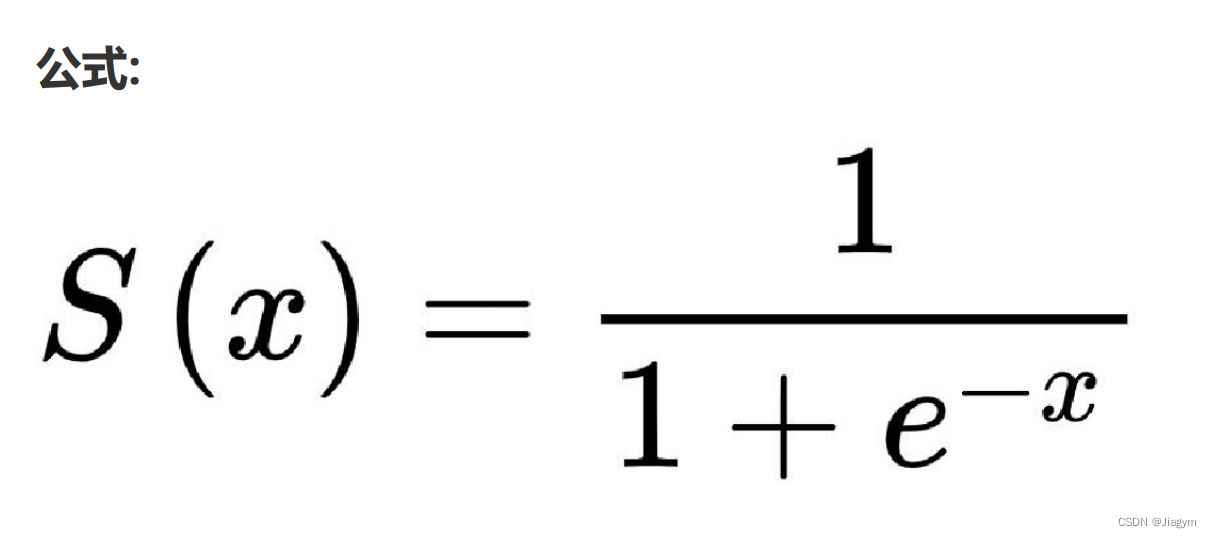
• 优点:
  将很大范围内的输入特征值压缩到0 – 1之间，使得在深层网络中可以保持数据幅度不会出现较大的变化；
  在物理意义上最为接近生物神经元；
  根据输出范围，该函数适用于将预测概率作为输出的模型；
• 缺点：
  当输入非常大或非常小的时候，输出基本为常数，即变化非常小，进而导致梯度接近于0；
  对于Sigmoid函数而言，其输出值域为(0, 1)，因此它的输出不是以0为中心的。这意味着Sigmoid激活函数的输出总是正的，不存在负值，所以其平均值永远大于0。

# S(x) = 1 / (1 + np.e ** (-x))
# 导数：S'(x) = S(x) * （1 - S(x)）
x = np.arange(-10, 10, 0.01)
sigmoid = 1 / (1 + np.e ** (-x))
dsigmoid = sigmoid * (1 - sigmoid)
plt.plot(x, sigmoid)
plt.plot(x, dsigmoid)
plt.show()

4.2激活函数：ReLu（线性整流函数)

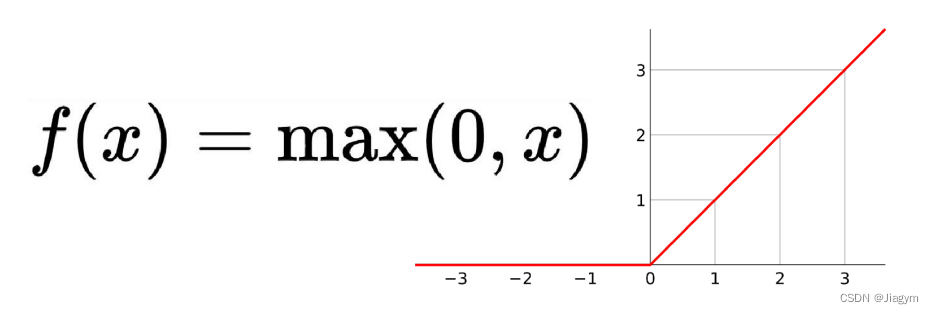
线性整流函数（Rectified Linear Unit, ReLU），在输入大于0时，直接输出该值；在输入小于等于 0时，输出 0。其作用在于增加神经网络各层之间的非线性关系。

• 优点：
  相较于sigmoid函数以及Tanh函数来看，在输入为正时，Relu函数不存在饱和问题。(即解决了梯度消失问题，使得深层网络可训练)；
  计算速度非常快，只需要判断输入是否大于0值；
  收敛速度远快于sigmoid以及Tanh函数；（备注:"收敛速度"是指训练神经网络时模型的参数如何逐渐接近最优解或理想值的速度）
  当输入为正值，导数为1，在“链式反应”中，不会出现梯度消失
• 缺点：
  存在Dead Relu Problem，即某些神经元可能永远不会被激活(输出永远是零)，进而导致相应参数一直得不到更新；
  Relu函数的输出不是以0为均值的函数；

x = np.arange(-10, 10, 0.1)
# 用于逐位比较取最大值
y = np.maximum(0, x)
plt.plot(x, y)
plt.show()

4.3Softmax(归一化指数函数)

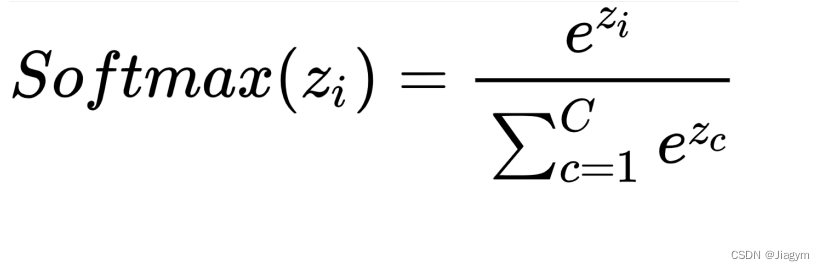
先了解下面的概念(后续深度学习会讲解,当前只需要知道这是一个函数。
softmax通常在多分类问题中用于神经网络的输出层。它的主要作用是将神经网络的原始输出转换为类别概率分布。
Softmax函数可以将数据转化为(0,1)之间的数值

# 输出值在(0, 1)，当做概率分布。
# np.exp(z) / np.sum(np.exp(z))

import matplotlib.pyplot as plt
import numpy as np
z = np.arange(-10, 10, 0.01)
y = np.exp(z) / np.sum(np.exp(z))
plt.plot(z, y)
plt.show()

4.4 激活函数：tanh（双曲正切）

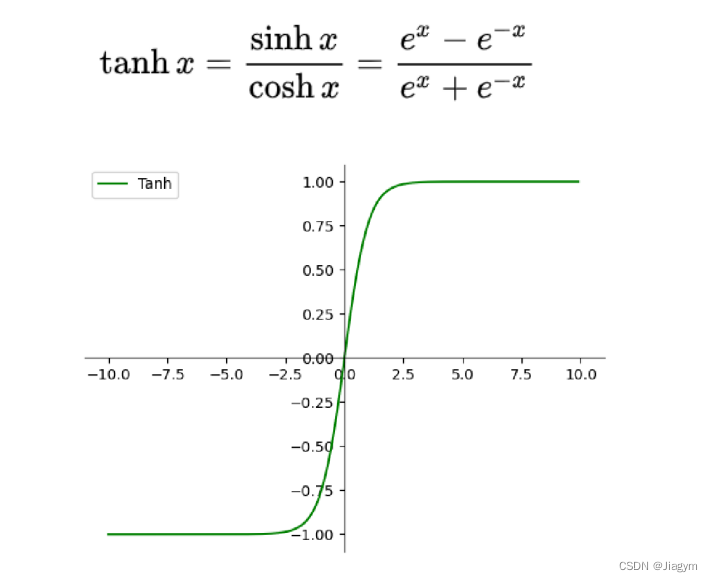
双曲函数，tanh为双曲正切，由双曲正弦和双曲余弦这两种基本双曲函数推导而来。

• 优点：
  解决了的Sigmoid函数输出不是0均值的问题;
  在神经网络中，我们希望网络在训练过程中能够适应数据的分布，不要偏向某个方向。零中心性使得梯度在正负方向上有较大的动态范围，更有利于网络参数的更新，有助于更好地适应数
  据分布，提高训练效果。
  tanh 的输出范围在 [-1, 1] 之间，相对于 sigmoid 来说，输出的动态范围更大;
  在原点附近，tanh函数与y=x函数形式相近，使得当激活值较低时，训练相对容易;
• 缺点：
  与Sigmoid函数类似，梯度消失问题仍然存在；

5 泰勒展开

泰勒展开是一种将一个函数表示为无限级数的方法，通常用于在某个点附近近似表示函数。泰勒展开的条件是函数必须在展开的点处具有足够多的可导性。
泰勒展开https://www.geogebra.org/m/qSeU7zV7

# b + w1 * x + w2 * x^2 + w3 * x^3 + w4 * x^4...

6. 极限

极限是微积分的基础概念，指无限靠近而永远不能到达。

7.微分积分

通过将区域划分成无穷小的小块，然后对这些小块进行求和来逼近曲线下的面积。具体而言，我们可以将曲线下的区域划分成许多极小的矩形，计算每个矩形的面积，然后将所有矩形的面积相加。当我们将这些小矩形的宽度趋近于零时，就得到了一个极限值，这个极限值即为曲线下的面积。
数学上，这个过程可以用积分来表示。定积分就是通过求和小块的面积，然后取极限的方式来计算曲线下的面积。这种方法在处理复杂的曲线、曲面等几何形状时非常强大，使得我们可以更精确地计算它们的面积。

8. 导数

8.1 导数（微分）

导数是代表函数（曲线）的斜率，是描述函数（曲线）变化快慢的量，同时曲线的极大值点也可以使用导数来判断，即极大值点的导数为0，此时斜率为零。

• 导数：
  用来分析函数的变化率，是曲线的斜率。（单调递增、单调递减）；
  若导数大于零，则单调递增；若导数小于零，则单调递减若已知函数为递增函数，则导数大于等于零
• 二阶导数：
  是斜率的变化，表现曲线是凹凸性（拐点），是斜率的斜率；
  定理：若函数在某区间内二阶可导，二阶导数 f’‘(x)>0，则函数在此区间上是凹的；二阶导数 f’'(x)<0，则函数在此区间上是凸的。
• 梯度(斜率、斜度)：
  导数的几何形态(通俗地解释为函数图像上某一点处的切线的斜率)。

导数的几何意义:
设函数y = f(x)的图像如图所示。AB为过点A(x0, f(x0)) 与B(x0+∆x, f(x0+∆x))的一条割线。此割线的斜率是∆y/∆x = (f(x0+∆x) - f(x0)) / ∆x, 割线的斜率就是函数的平均变化率。
当点B沿曲线趋近于点A时，割线AB绕点A转动，到直线AD。这条直线AD叫做此曲线在点A的切线
当∆x—>0 就是切线AD的斜率曲线某一点处切线的斜率就反映曲线在这一点的变化率。

8.2 复合函数求导

比如：已知房屋面积， 估计成交价格。价格只取决于面积，当前面积就是自变量，价格就是因变量。因变量的值只取决于一个自变量的函数，称为一元函数。y=x^2
实际情况决定房屋的价格还依赖于地理位置、交通等因素。这些因素也可以成为自变量。自变量不止一个函数被称为多元函数。通常使用f(x, y, z)或g(x, y)等形式表示多元函数，比如:f(x, y, z) = xy+yz+zx是一个三元函数, g(x, y) = x^2 + y^2 表示一个二元函数。那二元函数导数怎么求? 这就引出了偏导数。

9. 偏导数

二元函数：z = f(x, y) 对y求偏导数，就把其他自变量（x）作为常数，求导。
导数是函数值关于自变量的变化率，多元函数有多个自变量，关于某个自变量的变化率就是多元函数对这个自变量的偏导数。
比如，房价 与面积、地理位置还有交通三个因素相关，那么地理位置和交通确定时，房价关于面积的变化率就是价格对面积的偏导数。
使用符号∂f(x,y,z)/∂x.表示多元函数（x,y,z）对自变量x的偏导数。那么，y和z的偏导数可以表示为∂f(x,y,z)/∂y和∂f(x,y,z)/∂z。
简单来说，关于某个变量的偏导数就是将其他变量看做常数，按照求导法则进行求导即可。
比如: f(x,y)=x^2+ y^2 关于x的偏导数 f’x(x, y) = 2x

10. 梯度

函数在某一处沿着不同的方向运动，函数值的变化率不同。梯度可以定义为一个函数的全部偏导数构成的向量，梯度向量的方向是函数值变化率最大的方向。
简单理解就是对于函数某个特定点，它的梯度就表示从该点出发，函数值变化最迅猛的方向。
使用符号▽表示函数的梯度。二元函数f(x, y) 的梯度就是对x, y 求偏导数组成的二维向量, 三元函数g(x, y, z), 梯度为x, y , z求偏导数组成的三维向量。
对于单变量的函数，梯度即为导数，按照导数的方法计算梯度即可。
比如:
二元函数f(x, y）=x^2+y2，梯度是 (2x, 2y)，那么在点(1, 1)处的梯度向量为(2, 2)，在点(1, 1)处沿该向量变化，函数值变化最快。
如果按照向量(-1, 0)的方向移动一个1个单位，到达(0, 1), 函数值为0²⁺¹2=1, 比f(1, 1) 减小1。换另一个方向，按照向量(1, 0)的方向移动1到达(2, 1) 函数值为2²⁺¹2=5 比f(1, 1) 增加3按照梯度方向(2, 2) 移动1，大约到达(1.7, 1.7),函数值为1.7^2 +1.7^2 = 5.78 比f(1, 1) 增加3.78。所以按照梯度方向移动，函数增加最迅猛。

11. 梯度下降算法

解决问题: 通过迭代的方法找到目标函数的最小值

前面学过， 导数可以求解最小值。那现在为什么又需要使用梯度下降算法求解最小值呢？
因为如果目标函数非常复杂，计算函数的导数会很困难。

“回归”最初由19世纪的统计学家弗朗西斯·高尔顿（FrancisGalton）引入，源于他对父母和子女身高之间关系的研究。在他的研究中，他发现子女的身高倾向于“回归”（regress）到整体人群的平均身高。
这个词的选择是有历史渊源的，它反映了弗朗西斯·高尔顿当时的研究目标。具体来说，在统计学中，“回归”这个词的含义是，指代（或观测值）的某一特征倾向于“回归”到总体均值，即趋向于平均值。因此，线性回归模型的目标是找到一个线性关系，使得观测值与总体均值的差异最小化。

1）定义模型 g(x) =ωx+b
我们现在想通过一条线直线( g(x) = ωx+b )描述这种关系。因为当前只有一个自变量所以是一元线性函数回归问题(目标是预测一个连续值输出)
现在当 ω , b取不同值的时候如下图所示

当调整到一定程度的时候，很难从直观上看出那一条线更符合这种描述关系当前怎么办?引出均方误差， 通过均方误差得到合适的 ω 和 b
2） 定义均方误差损失函数
均方误差是反映真实值和预测值之间差异的一种度量关系，均方误差越小这条线越合适, 由均方误差我们可以得到一个误差函数

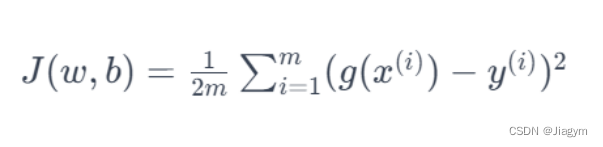
这个误差函数因为 x 和 y是已知 的，问题就转为求 ω 和 b， 使得损失函数最小。
将g(x) = ωx+b 带入得

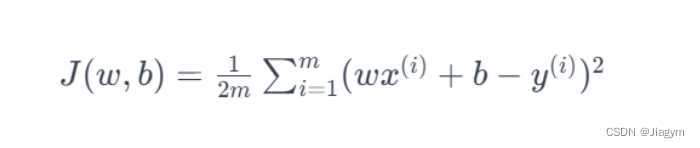
可以分别看成是关于 ω 与 b 的二次函数
3）计算梯度
其中 m 是样本数量，x(i) 是第 i 个样本的特征，y(i) 是对应的实际值。现在我们计算 J 对 ω 和 b 的偏导数

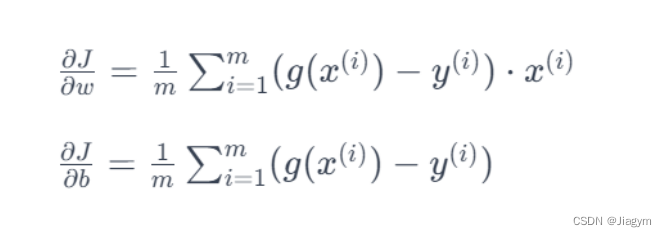
4）参数更新
给定一个初始值，朝着梯度反方向移动，函数值下降最快。
数学公式:

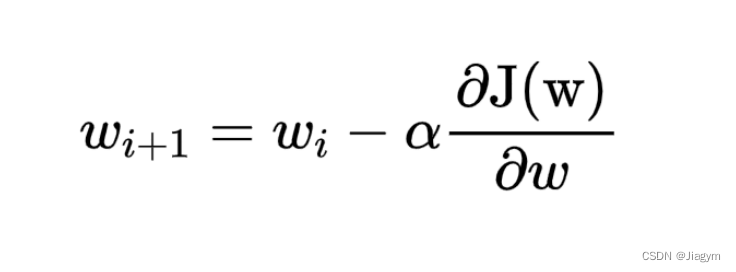
ωi+1: 表示下一个值
ωi: 表示当前值
-(负号)： 梯度的反方向
α: 学习率或者步长，控制每一步移动的距离，不能太大，太大移动比较快回会错过最佳点，太小移动较慢时间比较长。
梯度: 函数变化最快的点

梯度下降算法是一种用于优化函数的迭代优化算法，主要用于调整模型参数以最小化一个损失函数。这个算法的核心思想是通过计算损失函数的梯度，沿着梯度的负方向更新参数，以便逐步接近最优解。以下是梯度下降算法的基本原理：

1. 目标函数与损失函数：
   假设有一个目标函数（也称为损失函数）J(θ)，其中 θ 表示模型的参数。我们的目标是找到一组参数 θ，使得 J(θ) 取得最小值。
2. 梯度的方向：
   梯度是目标函数在某一点的导数，它指示了函数在该点上升最快的方向。梯度的负方向是函数下降最快的方向。
3. 参数更新：
   梯度下降的更新规则如下：
   θ:=θ−α*∇J(θ)
   其中：
   α 是学习率，控制每次参数更新的步长
   ∇J(θ) 是目标函数在当前参数值 θ 处的梯度
4. 迭代过程
   重复执行参数更新步骤，直到满足停止条件（例如达到指定的迭代次数）。

梯度下降算法要点：

1. 设置学习率
2. 求解梯度
3. 梯度参数更新
4. w = w - a * 梯度

简而言之：主要是确定方向和步长

# 梯度下降算法
import random
import matplotlib.pyplot as plt
w = random.random()
b = random.random()
_x = [i/100 for i in range(100)]
_y = [3*k + 10 + random.random() for k in _x]
learn_ratio = 0.1
for i in range(1000):
    for x, y in zip(_x, _y):
        h = w * x + b
        loss = (y-h)**2

        dw = -2 * x * (y-h)
        db = -2 * (y-h)

        w -= dw * learn_ratio
        b -= db * learn_ratio
        print(f'loss:{loss}---w:{w}---b:{b}')

        plt.ion()
        plt.cla()
        plt.plot(_x, _y, '.')
        plt.plot(_x, [w * m + b for m in _x])
        plt.pause(0.01)

plt.show()
plt.pause(0)

12.回归问题

根据输出类型的不同，预测问题主要分为:
分类问题：输出变量为有限个离散变量，当个数为 2 时即为最简单的二分类问题；
回归问题：输入变量和输出变量均为连续变量；

机器学习的主要任务:
• 分类任务：classification
• 回归任务：regression

两者的的预测目标变量类型不同，回归问题是连续变量，分类问题离散变量。

13.监督学习与无监督学习

在人类的学习中，有的人可能有高人指点，有的人则是无师自通。在机器学习中也有类似的。根据训练数据是否具有标签信息，可以将机器学习的任务分成以下三类。
监督学习：基于已知类别的训练数据进行学习；
无监督学习：基于未知类别的训练数据进行学习；
半监督学习：同时使用已知类别和未知类别的训练数据进行学习。

14.正向/反向传播

正向传播是指对神经网络沿着从输入层到输出层的顺序

反向传播依据微积分中的链式法则，沿着从输出层到输入层的顺序，依次计算并存储神经网络各层的中间变量以及参数的梯度。