动态规划入门：从斐波那契数列开始的算法之旅

快速体验

1. 打开 InsCode(快马)平台 https://www.inscode.net
2. 输入框内输入如下内容：

   开发一个面向初学者的动态规划交互式学习应用，聚焦斐波那契数列问题：1) 展示递归解法的问题；2) 逐步引导理解备忘录优化；3) 过渡到标准的DP解法；4) 提供可视化调用栈和DP表填充过程；5) 包含简单练习题和即时反馈。使用纯前端实现（HTML/CSS/JS），确保无需后端即可运行。

3. 点击'项目生成'按钮，等待项目生成完整后预览效果

初识动态规划：从斐波那契数列说起

动态规划（Dynamic Programming，简称DP）是算法学习中一个既重要又让人头疼的概念。很多初学者第一次接触时都会感到困惑，但其实它的核心思想并不复杂。今天，我们就从最经典的斐波那契数列问题入手，一步步揭开动态规划的神秘面纱。

1. 递归解法：简单但低效

斐波那契数列的定义非常简单：第0项是0，第1项是1，从第2项开始，每一项都等于前两项之和。用代码实现这个定义，最直观的方式就是递归：

• 定义一个函数fib(n)，如果n小于2直接返回n
• 否则返回fib(n-1) + fib(n-2)

这种解法虽然正确，但效率极低。计算fib(5)时，fib(3)会被计算多次；计算fib(20)时，这种重复计算会更加严重。这就是所谓的"重叠子问题"，是动态规划要解决的核心问题之一。

2. 备忘录优化：空间换时间

为了减少重复计算，我们可以引入一个"备忘录"（memoization）来存储已经计算过的结果：

• 创建一个数组或对象来记录已经计算过的fib(n)值
• 每次计算fib(n)前先查备忘录，如果存在就直接返回
• 否则进行计算，并将结果存入备忘录

这种方法将时间复杂度从指数级O(2^n)降到了线性O(n)，是动态规划思想的初步体现。

3. 标准DP解法：自底向上

动态规划的正式解法通常是"自底向上"的迭代方法：

1. 定义一个数组dp，dp[i]表示第i个斐波那契数
2. 初始化dp[0]=0，dp[1]=1
3. 从2到n依次计算dp[i] = dp[i-1] + dp[i-2]
4. 最后返回dp[n]

这种方法同样具有O(n)的时间复杂度，但省去了递归的开销，是更标准的动态规划实现。

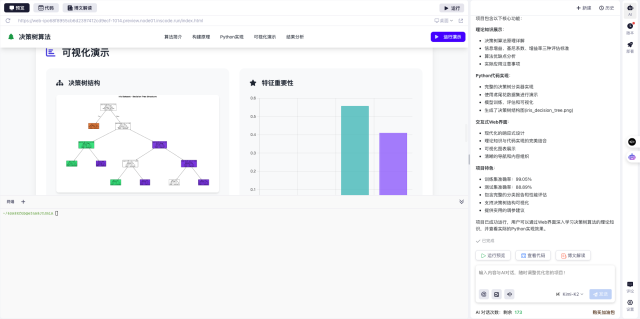
4. 可视化理解：调用栈与DP表

为了更直观地理解这些解法，我们可以借助可视化工具：

• 递归调用栈：展示递归解法中函数的层层调用关系
• DP表填充过程：动态展示自底向上解法中dp数组的填充过程

这些可视化效果能帮助初学者更清晰地看到算法的运行机制，理解动态规划如何通过保存子问题的解来优化效率。

5. 练习与反馈

为了巩固学习效果，一个好的学习应用应该包含：

• 基础练习：让用户手动完成斐波那契数列的DP解法
• 即时反馈：对用户的解答进行验证和提示
• 延伸思考：引导用户思考如何将空间复杂度优化到O(1)

为什么选择前端实现？

这个学习应用采用纯前端技术(HTML/CSS/JS)实现有几个优势：

1. 无需后端服务器，打开浏览器就能运行
2. 可视化效果可以更直观地展示算法过程
3. 交互式学习体验更好，用户可以实时修改参数观察效果

在InsCode(快马)平台上的体验

我在InsCode(快马)平台上实践这个项目时，发现它的编辑器响应很快，预览功能也很方便。最棒的是，这类前端项目可以直接一键部署，生成一个可公开访问的链接，方便分享给其他人学习。

对于算法学习者来说，能够即时看到代码的运行效果，比只看静态的代码要直观得多。如果你也想动手实践动态规划算法，不妨从这里开始你的算法之旅。

快速体验

1. 打开 InsCode(快马)平台 https://www.inscode.net
2. 输入框内输入如下内容：

   开发一个面向初学者的动态规划交互式学习应用，聚焦斐波那契数列问题：1) 展示递归解法的问题；2) 逐步引导理解备忘录优化；3) 过渡到标准的DP解法；4) 提供可视化调用栈和DP表填充过程；5) 包含简单练习题和即时反馈。使用纯前端实现（HTML/CSS/JS），确保无需后端即可运行。

3. 点击'项目生成'按钮，等待项目生成完整后预览效果