状态机动态规划之股票问题

卖股票的最佳时机 III

题目

给定一个数组，它的第 i 个元素是一支给定的股票在第 i 天的价格。设计一个算法来计算你所能获取的最大利润。你最多可以完成 两笔 交易。注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

示例

示例1

输入：prices = [3,3,5,0,0,3,1,4]

输出：6

解释：在第 4 天（股票价格 = 0）的时候买入，在第 6 天（股票价格 = 3）的时候卖出，这笔交易所能获得利润 = 3-0 = 3 。随后，在第 7 天（股票价格 = 1）的时候买入，在第 8 天 （股票价格 = 4）的时候卖出，这笔交易所能获得利润 = 4-1 = 3 。

示例2

输入：prices = [1,2,3,4,5]

输出：4

解释：在第 1 天（股票价格 = 1）的时候买入，在第 5 天 （股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。注意你不能在第 1 天和第 2 天接连购买股票，之后再将它们卖出。因为这样属于同时参与了多笔交易，你必须在再次购买前出售掉之前的股票。

状态表示数组和状态转移

在这道题目当中我们也是二维数组进行状态的表示，二维数组为dp[N][5]，5表示我们有5个状态，dp[N][i]表示第N天的第i个状态能够多大的收益！（为了方便下面介绍，假设一天有一个股票，dp[N][]表示第N天的状态，对应第N个股票的状态）

• dp[N][0]，表示第N天一次买入和卖出的操作都没有过，那么dp[N][0] = dp[N - 1][0]，跟前一天的状态一样，都没有进行股票的买入和卖出，其实也可以直接令dp[N][0] = 0，因为没有进行操作我们的收益肯定等于0。
• dp[N][1]，表示第N天已经进行过第一次买入，这个买入可以是在第N天进行买入，也可以在前面N-1天买入，然后在第N天保持状态。如果第N天刚刚进行买入，那么我们的收益就是从前一天一次买入和卖出都没有操作转移过来的，那么就有dp[N][0] - prices[i]，因为根据上面的分析dp[N][0] = 0，那么直接让dp[N][1] = -prices[i]即可。如果在前N-1天已经进行了买入，那么在第N天就不行操作，即在第N天收入为0，即dp[N][1] = dp[N - 1][1]。
• dp[N][2]，表示第N天已经进行过第一次卖出，这个状态可以是在第N天进行卖出，也可以是在前面N-1天已经卖出，然后在第N天保持状态如果在第N天进行第一次卖出那么我们在第N天的收益就等于prices[i]，再加上前N-1天买入一次的收益，即dp[N][2] = dp[N - 1][1] + prices[i]。如果前N-1天已经卖出，那么直接保持状态即可，我们在第N天的收益就为0，那么dp[N][2] = dp[N - 1][2]。
• dp[N][3]，表示第N天已经进行过第二次买入，这个状态可以是在第N天进行买入，也可以是在前面N-1天买入，然后在第N天保持状态。如果在第N天进行第二次买入那么我们在第N天的收益就等于-prices[i]，再加上前N-1天买入卖出一次的收益，即dp[N][3] = dp[N - 1][2] - prices[i]。如果前N-1天已经有了第二次买入的操作，那么直接保持状态即可，我们在第N天的收益就为0，那么dp[N][3] = dp[N - 1][3]。
• dp[N][4]，表示第N天已经进行过第二次卖出，这个状态可以是在第N天进行买入，也可以是在前面N-1天卖出，然后在第N天保持状态。如果是在第N天卖出，那么在第N天的收益为prices[i]，再加上前N-1天买入两次卖出一次的收益dp[N][3]，那么dp[N][4] = dp[N - 1][3] + prices[i]。如果是前N-1天已经买入卖出两次了，那么直接保持前一天的状态即可，即dp[N][4] = dp[N-1][4]。

根据上面的分析我们可以得到下面的状态机（状态转移图）：

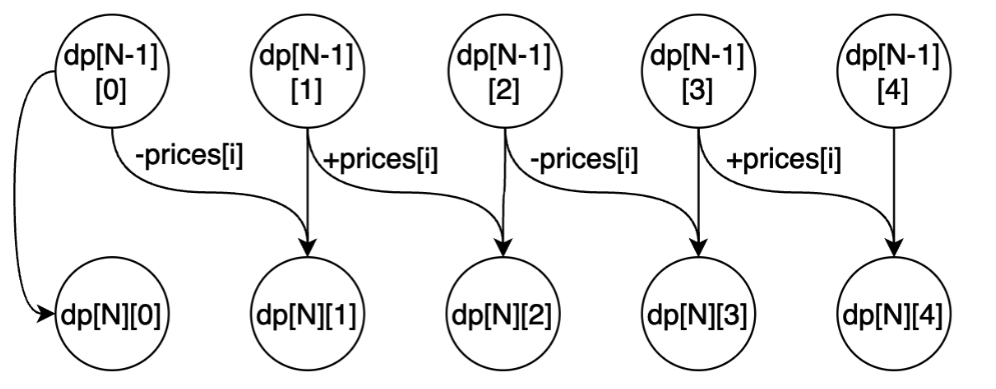
相信看到这里你就应该能够理解为什么这种动态规划叫做状态机动态规划，因为在这种动态规划当中数据存在很多状态，而我们需要进行仔细的分析，分析清楚这里面的状态该如何进行转移，进而分析出来各种状态之间的转移关系，这种模式跟状态机非常像，因此叫做状态机动态规划。

数据流依赖分析和状态转移方程

假如可以买卖股票的天数一共有N天，那么我们最终需要求出来的结果是dp[N][4]，表示第N天已经买入卖出2次，将两次使用的机会都是用完了，为什么我们最终的结果是dp[N][4]呢？这你可能疑惑万一我买入一次卖出一次能够得到的收益最大呢？我们是允许在同一天多次买入和卖出股票的，而在同一天买入和卖出股票收益为0，所以不影响最后的结果，因此买入卖出一次最终也可以转移到买入卖出两次（其中一次在同一天买入和卖出即可，我们在对数组进行初始化的时候就需要进行多次买入和卖出（可以看下文当中对数组初始化的分析）），因此我们最终需要返回的结果就是dp[N][4]。

而根据上面的分析我们知道，从上图可以看出转移到dp[N][4]这个状态一共有两种方式，我们应该选择转移之后两者方式得到的价值比较大的那个，即dp[N][4] = max(dp[N - 1][4], dp[N - 1][3] + prices[i]);，而dp[N - 1][4]的转移又有两种方式我们也应该选择其中较大的，dp[N - 1][3]也有两种转移方式，因此其也应该选择两者当中比较大的那个值，即dp[N][3] = max(dp[N - 1][3], dp[N - 1][2] - prices[N]);，同理我们可以得到其他状态的转移方程，每个数据都是需要选择转移之后价值最大的那个，最终我们的状态转移方程如下：

dp[i][0] = dp[i - 1][0];dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] - prices[i]);dp[i][2] = max(dp[i - 1][2], dp[i - 1][1] + prices[i]);dp[i][3] = max(dp[i - 1][3], dp[i - 1][2] - prices[i]);dp[i][4] = max(dp[i - 1][4], dp[i - 1][3] + prices[i]);

动态规划设计

在求解动态规划问题的时候通常的步骤有以下几个：

• 寻找能够表示状态的数组dp，即我们需要寻找dp的含义，分析需要用几纬数组表示具体的状态。
• 通过分析问题，寻找动态转移公式。
• 初始化状态数组。
• 通过分析动态转移方程，确定数组的遍历顺序。

综合上面的分析，我们的初始化代码如下：

dp[0][0] = 0;dp[0][1] = -prices[0];dp[0][3] = 0;dp[0][3] = -prices[0];dp[0][4] = 0;

根据状态转移方程，我们知道第i天依赖于第i-1天的数据，因此我们遍历的顺序为从前到后进行遍历。

代码

class Solution {  public int maxProfit(int[] prices) {    int[][] dp = new int[prices.length][5];    // dp[i][0] 表示一次买入和卖出都没有    // dp[i][1] 表示第一次买入    // dp[i][2] 表示第一次卖出    // dp[i][3] 表示第二次买入    // dp[i][4] 表示第二次卖出    dp[0][1] = -prices[0];    dp[0][3] = -prices[0];    for (int i = 1; i < prices.length; i++) {      dp[i][0] = dp[i - 1][0];      dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] - prices[i]);      dp[i][2] = Math.max(dp[i - 1][2], dp[i - 1][1] + prices[i]);      dp[i][3] = Math.max(dp[i - 1][3], dp[i - 1][2] - prices[i]);      dp[i][4] = Math.max(dp[i - 1][4], dp[i - 1][3] + prices[i]);    }    return dp[prices.length - 1][4];    // 注意数据之前传递依赖的关系    // 因为要求 dp[N][4] 当中    // 最大的值 因此需要求解 dp[N - 1][4] 和 dp[i - 1][3] 的最大值    // ......  }}

上面的代码的时间和空间复杂度分别为O(n)和O(n)。

空间复杂度优化

其实我们可以使用一个单行数组进行优化，优化代码如下：

class Solution {  public int maxProfit(int[] prices) {    int[] dp = new int[5];    dp[1] = -prices[0];    dp[3] = -prices[0];    for (int i = 1; i < prices.length; i++) {      dp[0] = dp[0]; // 这一行可以不要的 放在这里只是为了状态转移方程的完整      dp[1] = Math.max(dp[1], dp[0] - prices[i]);      dp[2] = Math.max(dp[2], dp[1] + prices[i]);      dp[3] = Math.max(dp[3], dp[2] - prices[i]);      dp[4] = Math.max(dp[4], dp[3] + prices[i]);    }    return dp[4];  }}

我们现在来简要分析一下上面的代码为什么可行：

比如现在i=3，现在要进行更新，现在的dp数组还是i=2的状态，如果用二维数组来表示的话，现在的单行数组中的dp[i]相当于二维数组当中的数据dp[2][i]，假如我们现在需要更新dp[3][2]，根据二维数组的动态转移方程，我们需要二维数组第二行的数据dp[2][2]，但是此时的单行数组当中的数据还没有更新，也就是说dp[2]等于 dp[2][2]（前面的dp表示单行数组，后面的dp表表示二维数组的dp），因此还是上一个状态的数据，因此更新没有问题。

dp[i][0] = dp[i - 1][0];dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] - prices[i]);dp[i][2] = max(dp[i - 1][2], dp[i - 1][1] + prices[i]);dp[i][3] = max(dp[i - 1][3], dp[i - 1][2] - prices[i]);dp[i][4] = max(dp[i - 1][4], dp[i - 1][3] + prices[i]);

根据上面的状态转移方程我们知道dp[3][2]依赖于dp[2][1]，而dp[2][1]相当于dp[1]，但是在下面的代码当中，我们在更新dp[2]之前dp[1]已经更新了，也就是说dp[1]已经是第三行的状态了，即dp[1] = dp[3][1]，而现在更新的时候需要的是第二行的状态，因此这就不对了。

class Solution {  public int maxProfit(int[] prices) {    int[] dp = new int[5];    dp[1] = -prices[0];    dp[3] = -prices[0];    for (int i = 1; i < prices.length; i++) {      dp[0] = dp[0]; // 这一行可以不要的 放在这里只是为了状态转移方程的完整      dp[1] = Math.max(dp[1], dp[0] - prices[i]);      dp[2] = Math.max(dp[2], dp[1] + prices[i]);      dp[3] = Math.max(dp[3], dp[2] - prices[i]);      dp[4] = Math.max(dp[4], dp[3] + prices[i]);    }    return dp[4];  }}

那为什么上面的代码又可行呢？

• 如果dp[1]是从上一行的dp[1]转移而来，那么就是符合我们的想法的，dp[2]使用的还是上一个(第2行)状态的dp[1]，因为本行状态的(第3行)dp[1]和第2行的dp[1]相等。
• 如果dp[1]是从dp[0] - prices[3]转移过来的，那么在这条语句dp[2] = Math.max(dp[2], dp[1] + prices[3]);当中，如果选择的是dp[2]那么也没关系，因为他跟dp[1]没有关系。如果选择的是dp[1] + prices[3]，那么也没关系因为dp[1]减去了prices[3]，这一加一减相当于没有收益，这并不影响最后的结果，因为这一卖一买都是在今天完成的，而对最终结果产生影响的肯定是在前面已经买入的操作（比如第2行的dp[1]就表示在之前进行第一次买入），而不会是在今天的买入，理解这一点就可以理解上的代码了。
• 其余代码的影响也是类似的，都可以通过一加一减低消掉，最终都不影响最后的结果。

通过上述的优化之后空间复杂度变为O(1)。

卖股票的最佳时机 IV

题目

给定一个整数数组 prices ，它的第 i 个元素 prices[i] 是一支给定的股票在第 i 天的价格。设计一个算法来计算你所能获取的最大利润。你最多可以完成 k 笔交易。注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

示例

示例1

输入：k = 2, prices = [2,4,1]

输出：2

解释：在第 1 天 (股票价格 = 2) 的时候买入，在第 2 天 (股票价格 = 4) 的时候卖出，这笔交易所能获得利润 = 4-2 = 2 。

示例2

输入：k = 2, prices = [3,2,6,5,0,3]

输出：7

解释：在第 2 天 (股票价格 = 2) 的时候买入，在第 3 天 (股票价格 = 6) 的时候卖出, 这笔交易所能获得利润 = 6-2 = 4 。随后，在第 5 天 (股票价格 = 0) 的时候买入，在第 6 天 (股票价格 = 3) 的时候卖出, 这笔交易所能获得利润 = 3-0 = 3 。

问题分析

这个问题和本文当中的第一个问题其实差不多，只不过上面的问题是最多完成两笔交易，而在这个问题当中是最多可以完成k笔交易，这个问题相当于上面问题的推广，我们再来分析一下上一道题目的动态转移公式：

dp[i][0] = dp[i - 1][0];dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] - prices[i]);dp[i][2] = max(dp[i - 1][2], dp[i - 1][1] + prices[i]);dp[i][3] = max(dp[i - 1][3], dp[i - 1][2] - prices[i]);dp[i][4] = max(dp[i - 1][4], dp[i - 1][3] + prices[i]);

上面的公式用一个公式表示就是：

dp[i][j]=max(dp[i−1][j],dp[i−1][j−1]±prices[i]);

现在我们将这个问题进行推广：

• 状态表示

• dp[i][0] 表示一次买入和卖出都没有。

• dp[i][2 * k - 1] 表示第 k 次买入。根据上文的分析，这个地方类似，有两种状态可以转换成第k次买入这个状态。如果前i-1天已经有k次买入了，则保持前面的状态就行，即dp[i][2 * k - 1] = dp[i - 1][2 * k - 1]。如果前i-1天已经有k-1次买入和卖出了，那么就需要进行买入，即dp[i][2 * k - 1] = dp[i - 1][2 * k - 2]- prices[i] 。

• dp[i][2 * k] 表示第 k 次卖出。同样的，也有两个状态可以转换成这个状态。如果前i-1天已经有k次卖出了，则保持前面的状态就行，即dp[i][2 * k] = dp[i - 1][2 * k]。如果前i-1天已经有k次买入，那么就需要进行买入，即dp[i][2 * k] = dp[i - 1][2 * k - 1] + prices[i]。

• 根据上面的分析，那么状态转移方程如下（其中j是偶数）：

• dp[i][j - 1] = max(dp[i - 1][j - 1], dp[i - 1][j - 2] - prices[i]);dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - 1] + prices[i]);

• 同理我们最终需要返回的结果就是dp[N][2 * k]。

• 数组初始化

• 根据我们的分析，在买入之前必须卖出，因此在第一行当中所有的买入状态的价值都是-pirces[0]，所有的卖出状态的价值都是0，因为买入之后再卖出就相当于没有买卖一样。

代码

class Solution {  public int maxProfit(int k, int[] prices) {    if (prices == null || prices.length == 0)      return 0;    int m = 2 * k + 1;    int[][] dp = new int[prices.length][m];    // dp[i][0] 表示一次买入和卖出都没有    // dp[i][2 * k - 1] 表示第 k 次买入    // dp[i][2 * k] 表示第 k 次卖出    for (int i = 1; i < m; i += 2) {      dp[0][i] = -prices[0];    }    for (int i = 1; i < prices.length; i++) {      dp[i][0] = dp[i - 1][0];      for (int j = 2; j < m; j += 2) {        dp[i][j - 1] = Math.max(dp[i - 1][j - 1], dp[i - 1][j - 2] - prices[i]);        dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - 1] + prices[i]);       }    }    return dp[prices.length - 1][2 * k];    // 注意数据之前传递依赖的关系  } }

总结

在本篇文章当中主要给大家介绍了另外两种股票问题，在这两个股票问题当中都有许多的状态，状态之间的转化也比较复杂，在仔细分析上面两个问题的状态转化之后相信你已经能够理解状态机动态规划了，这种含有比较复杂的状态之间的变化就叫做状态机动态规划，这种问题一般分析起来还是比较复杂的。