Golang实现：判断对称二叉树-优快云博客

本文探讨如何使用Golang解决数据结构与算法问题，具体是检查一棵二叉树是否具备镜像对称的特性。通过对二叉树的深度优先或广度优先遍历，可以有效地判断其对称性。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

对称二叉树
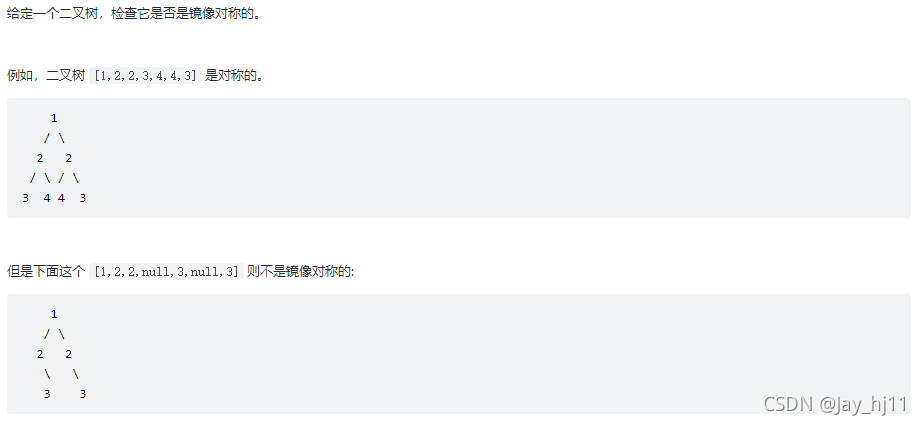
给定一个二叉树，检查它是否是镜像对称的。
在这里插入图片描述

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func isSymmetric(root *TreeNode) bool {

    // var check func(node1,node2 *TreeNode) bool
    // check = func(node1,node2 *TreeNode) bool{
    //    if node1==nil && node2 == nil {
    //       return true
    //    }
    //    if node1==nil || node2 == nil {
    //       return false
    //    }
    //    return node1.Val==node2.Val && check(node1.Left,node2.Right)&&check(node1.Right,node2.Left)
    // }
    return check(root,root)
}

func check(node1,node2 *TreeNode) bool{
    var q []*TreeNode
    q = append(q,node1)
    q = append(q,node2)
    for len(q) >0 {
        m,n := q[0],q[1]
        q=q[2:]
        if m == nil && n ==nil {
            continue
        }
        if m==nil || n == nil {
            return false
        }
        if m.Val != n.Val{
            return false
        }
        q = append(q,m.Left)
        q = append(q,n.Right)

        q = append(q,m.Right)
        q = append(q,n.Left)
    }
    return true
}

// func check(node1 *TreeNode,node2 *TreeNode)bool{
//     if node1==nil && node2 == nil {
//         return true
//     }
//     if node1==nil || node2 == nil {
//         return false
//     }
//     return node1.Val==node2.Val && check(node1.Left,node2.Right)&&check(node1.Right,node2.Left)
// }

对称二叉树 golang