矩阵高级
图形学应用
沿坐标轴延伸
矩阵可以表示某个图形,矩阵相乘实际上可以看做一个矩阵被另一个矩阵转换成其他图形的过程。如,
(
2.0
0
0
1.5
)
⋅
(
x
y
)
=
(
2
x
1.5
y
)
\begin{pmatrix}2.0&0\\0&1.5\end{pmatrix}\cdot\begin{pmatrix}x\\y\end{pmatrix}=\begin{pmatrix}2x\\1.5y\end{pmatrix}
(2.0001.5)⋅(xy)=(2x1.5y)
可以看做是在x方向扩大两倍,y方向扩大1.5倍。
沿坐标轴翻转
以二维空间为例,沿x轴翻转时横坐标不变,纵坐标取负数;同理,沿y轴翻转时纵坐标不变,横坐标取负数。当关于原点翻转时,横纵坐标均取负数。
旋转变换
旋转操作是比较复杂的变化,旋转某个角度后,横纵坐标均改变。 需要三角函数的基础,首先需要推导的是旋转θ角度后的点坐标,
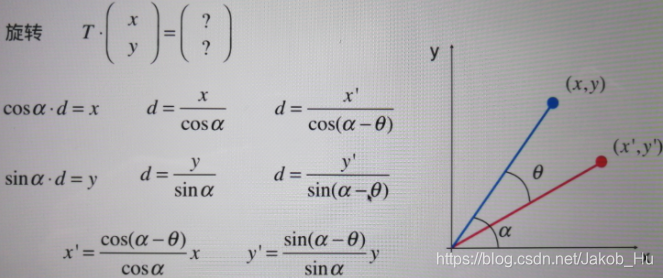
上式可进一步化简,

同理推导旋转后的y’点坐标,

于是旋转角度θ后的坐标变为,以二维空间为例,
T
⋅
(
x
y
)
=
(
x
⋅
c
o
s
θ
+
y
⋅
s
i
n
θ
−
x
⋅
s
i
n
θ
+
y
⋅
c
o
s
θ
)
T\cdot \begin{pmatrix}x\\y\end{pmatrix}= \begin{pmatrix}x\cdot cos\theta+y\cdot sin\theta\\-x\cdot sin\theta+y\cdot cos\theta\end{pmatrix}
T⋅(xy)=(x⋅cosθ+y⋅sinθ−x⋅sinθ+y⋅cosθ)
单位矩阵
单位矩阵都是方阵,其主对角线元素均为1,其余元素都为0。单位矩阵记为 I I I。
单位矩阵的性质
I
⋅
A
=
A
I\cdot A = A
I⋅A=A
A
⋅
I
=
A
A\cdot I = A
A⋅I=A
I
T
=
I
I^T=I
IT=I
单位矩阵就像是数字系统中的1,任意矩阵与其相应的范围矩阵相乘得到的结果依旧是矩阵本身。
代码实现
在之前的Matrix类中定义一个类方法,用于实现单位矩阵,
@classmethod
def identity(cls, n):
"""返回一个n×n维度的单位矩阵"""
m = [[0] * n for _ in range(n)]
for i in range(n):
m[i][i] = 1
return cls(m)
numpy中的单位矩阵
import numpy as np
# 得到一个2×2的单位矩阵
I = np.identity(2)
矩阵的逆(重点)
概念
在数字系统中,一个标量的逆可以看做是其倒数,假设存在一个不为0的值 k,
k
⋅
1
k
=
1
k\cdot \frac{1}{k}=1
k⋅k1=1
同理,在线性代数中,单位矩阵可以看做是“1”,所以一个矩阵A的逆矩阵B可以定义为,
A
⋅
B
=
B
⋅
A
=
I
A\cdot B=B\cdot A=I
A⋅B=B⋅A=I
在数字系统中,并不是所有的标量都有逆(数字0就没有)。
在矩阵中也是这样,很多矩阵都不存在逆矩阵。所以对于一个矩阵 A A A,如果存在一个矩阵 B B B满足 B A = A B = I BA = AB = I BA=AB=I,则称矩阵 A A A为可逆矩阵或非奇异矩阵 。反之,不存在逆矩阵的矩阵称为不可逆矩阵或奇异矩阵。
进一步细分,
- B是A的左逆矩阵,
B ⋅ A = I B\cdot A=I B⋅A=I - C是A的右逆矩阵,
A ⋅ C = I A\cdot C=I A⋅C=I
左逆矩阵和右逆矩阵并不都是同时存在的,如果一个矩阵A既存在左逆矩阵,同时也存在右逆矩阵,则 B=C。对这个结论进行证明,如下
B ⋅ A = I B\cdot A=I B⋅A=I A ⋅ C = I A\cdot C=I A⋅C=I
B ( A C ) = B I B(AC)=BI B(AC)=BI
( B A ) C = B (BA)C=B (BA)C=B
I C = B IC=B IC=B
C = B C=B C=B
综合上面的证明,可逆矩阵一定是方阵。一个非方阵一定不可逆。
此时可以解决幂矩阵的问题,
A
0
=
I
A^0=I
A0=I
A
−
1
=
A
的
逆
A^{-1}=A的逆
A−1=A的逆
A
−
2
=
(
A
−
1
)
2
,
即
A
的
逆
矩
阵
的
平
方
运
算
A^{-2}=(A^{-1})^2,即A的逆矩阵的平方运算
A−2=(A−1)2,即A的逆矩阵的平方运算
矩阵的性质
- 逆矩阵唯一性:矩阵中 AB = BA = I,则B是A的逆矩阵,且对于矩阵A,如果存在逆矩阵B,则B唯一。使用反证法针对唯一性进行证明,
假设A存在两个不同的逆矩阵B和C,
B ⋅ A = A ⋅ C = I B\cdot A=A\cdot C=I B⋅A=A⋅C=I
B ( A B ) = B ( A C ) B(AB)=B(AC) B(AB)=B(AC)
C = B C=B C=B
与基本假设相背离,故证明了逆矩阵的唯一性。 - 一个矩阵A的逆矩阵的逆是A,用公式表示为,
(
A
−
1
)
−
1
=
A
(A^{-1})^{-1}=A
(A−1)−1=A,证明如下,
假设 X − 1 = A X^{-1}=A X−1=A,
只需证明: X ⋅ A = I = A ⋅ X X\cdot A=I=A\cdot X X⋅A=I=A⋅X
A − 1 ⋅ A = I = A ⋅ A − 1 A^{-1}\cdot A=I=A\cdot A^{-1} A−1⋅A=I=A⋅A−1 - 矩阵乘法的逆
( A ⋅ B ) − 1 = B − 1 ⋅ A − 1 (A\cdot B)^{-1}=B^{-1}\cdot A^{-1} (A⋅B)−1=B−1⋅A−1 - 矩阵的逆与转置结合
( A T ) − 1 = ( A − 1 ) T (A^T)^{-1}=(A^{-1})^T (AT)−1=(A−1)T
对于该结论的证明需要用到矩阵转置中提及的性质 ( A ⋅ B ) T = B T ⋅ A T (A\cdot B)^T=B^T\cdot A^T (A⋅B)T=BT⋅AT,给出证明如下,
A T ⋅ ( A − 1 ) T = ( A − 1 ⋅ A ) T = I T = I A^T\cdot (A^{-1})^T=(A^{-1}\cdot A)^T=I^T=I AT⋅(A−1)T=(A−1⋅A)T=IT=I
( A − 1 ) T ⋅ A T = ( A ⋅ A − 1 ) T = I T = I (A^{-1})^T\cdot A^T=(A\cdot A^{-1})^T=I^T=I (A−1)T⋅AT=(A⋅A−1)T=IT=I
numpy中矩阵的逆
# numpy中的逆矩阵
A = np.array([[1, 2], [3, 4]])
invA = np.linalg.inv(A)
# 得到 [[-2.0, 1.0],
# [1.5, -0.5]]
# 如果对非方阵求取逆矩阵会报错
B = np.array([[1, 2, 3], [4, 5, 6]])
invB = np.linalg.inv(B)
用矩阵表示空间
回顾线性系统
这是矩阵高级应用的核心,空间视角是看待矩阵的关键。空间也是线性代数的核心。
先前提及到线性系统,实际上是将线性方程组换成是矩阵和向量相乘的形式,这种形式下存在两种视角,分别是行向量和列向量视角。先将一个线性方程组进行分解得到一个矩阵和一个向量。
{
x
+
2
y
=
3
4
x
+
5
y
=
6
\begin{cases}x+2y=3\\4x+5y=6\end{cases}
{x+2y=34x+5y=6
(
1
2
4
5
)
⋅
(
x
y
)
=
(
3
6
)
\begin{pmatrix}1&2\\4&5\end{pmatrix}\cdot \begin{pmatrix}x\\y\end{pmatrix}=\begin{pmatrix}3\\6\end{pmatrix}
(1425)⋅(xy)=(36)
行视角和列视角
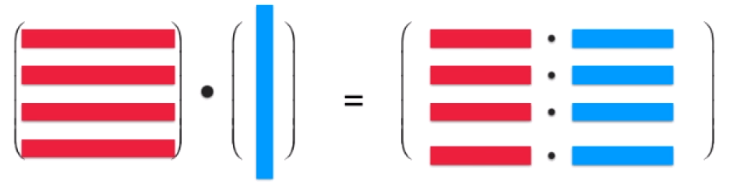
- 行视角
( 1 2 4 5 ) ⋅ ( x y ) = ( x + 2 y 4 x + 5 y ) \begin{pmatrix}1&2\\4&5\end{pmatrix}\cdot \begin{pmatrix}x\\y\end{pmatrix}=\begin{pmatrix}x+2y\\4x+5y\end{pmatrix} (1425)⋅(xy)=(x+2y4x+5y)
图形总结,
- 列视角
( 1 2 4 5 ) ⋅ ( x y ) = ( 1 4 ) x + ( 2 5 ) y \begin{pmatrix}1&2\\4&5\end{pmatrix}\cdot \begin{pmatrix}x\\y\end{pmatrix}=\begin{pmatrix}1\\4\end{pmatrix}x+\begin{pmatrix}2\\5\end{pmatrix}y (1425)⋅(xy)=(14)x+(25)y
图形总结,

列向量的视角审视矩阵代表的空间是更直观的,以一个最基本的例子作为引入,
(
1
0
0
1
)
⋅
(
x
y
)
=
(
1
0
)
x
+
(
0
1
)
y
=
x
⋅
e
1
⃗
+
y
⋅
e
2
⃗
\begin{pmatrix}1&0\\0&1\end{pmatrix}\cdot \begin{pmatrix}x\\y\end{pmatrix}=\begin{pmatrix}1\\0\end{pmatrix}x+\begin{pmatrix}0\\1\end{pmatrix}y=x\cdot\vec{e_1}+y\cdot\vec{e_2}
(1001)⋅(xy)=(10)x+(01)y=x⋅e1+y⋅e2
其中
e
1
⃗
\vec{e_1}
e1和
e
2
⃗
\vec{e_2}
e2分别代表的是平面坐标系的两个标准单位向量(实际上就是x和y轴的方向),所以该矩阵表示的是一个完整的平面坐标空间。
将这一思想进一步拓展,对于任意一个矩阵和一个向量的乘法,
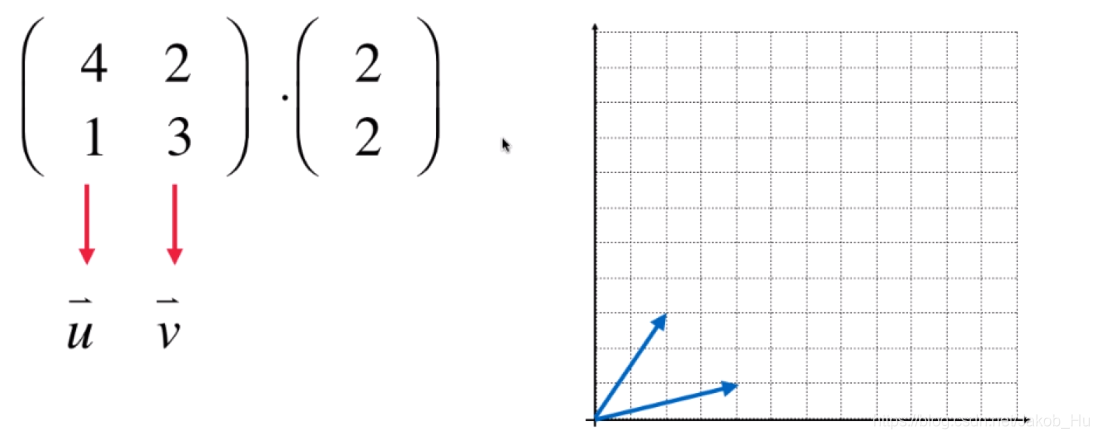
实际上可以看作是
u
⃗
\vec{u}
u和
v
⃗
\vec{v}
v两个向量定义了一个不同于标准单位向量所定义的空间。以上面的乘法为例,可以视为向量
u
⃗
=
(
4
,
1
)
\vec{u}=(4,1)
u=(4,1)和
v
⃗
=
(
2
,
3
)
\vec{v}=(2,3)
v=(2,3)v定义了一个新的空间,与
(
2
,
2
)
(2, 2)
(2,2)这个向量相乘的结果可以转化如下,

沿着
u
⃗
\vec{u}
u和
v
⃗
\vec{v}
v两个坐标轴的方向延伸2倍,最终得到上面(12, 8)这个结果。
为方便理解将上面的右图的坐标系进行改进,
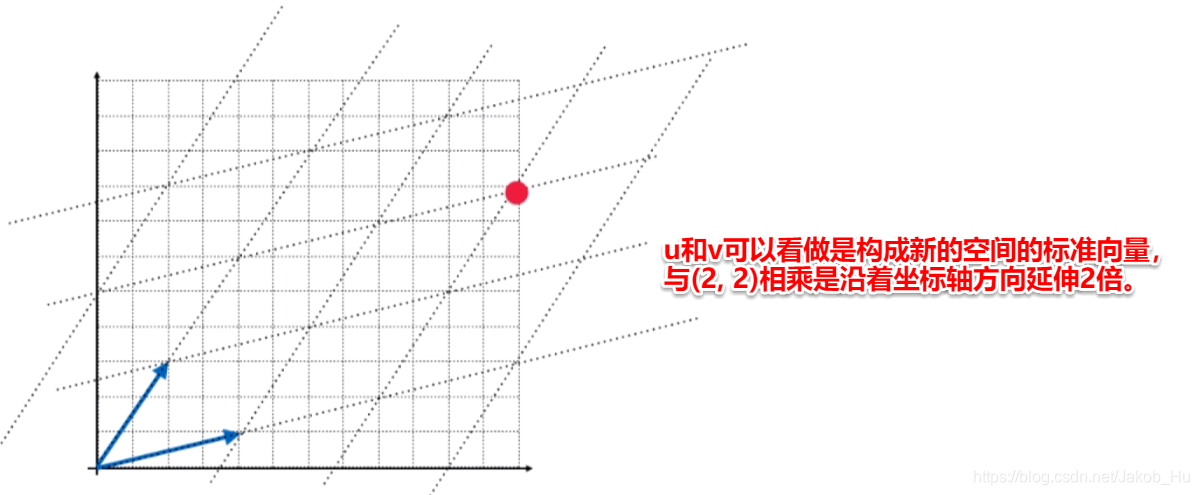
这种思想可以继续向n维空间拓展,表示n维空间的矩阵维度是 n×n,故矩阵表示空间使用的是方阵。







 博客围绕图形学中的矩阵应用展开,介绍了沿坐标轴延伸、翻转、旋转变换等图形学应用,阐述了单位矩阵的性质与代码实现,重点讲解矩阵的逆的概念、性质及在numpy中的应用,还从行视角和列视角探讨了用矩阵表示空间,强调空间视角是矩阵高级应用的关键。
博客围绕图形学中的矩阵应用展开,介绍了沿坐标轴延伸、翻转、旋转变换等图形学应用,阐述了单位矩阵的性质与代码实现,重点讲解矩阵的逆的概念、性质及在numpy中的应用,还从行视角和列视角探讨了用矩阵表示空间,强调空间视角是矩阵高级应用的关键。
















 1114
1114

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








