二叉树前中后序遍历的非递归版本-优快云博客

本文介绍了如何使用非递归方式遍历二叉树，通过栈来处理前序、中序和后序遍历。核心思路是将树分为左路节点和左路节点的右子树，利用栈进行操作。在前序遍历中，先压入节点并访问，然后处理左子树；中序遍历时，先压入节点的左子树，遇到空节点时回溯并访问；后序遍历则需判断右子树或前一个节点是否为空，以确定何时访问节点。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

主要思路

非递归遍历二叉树的思路有很多，这里用到的思路有一个优点，前中后序遍历的思路大差不差。

我们这里用到的思路就一条，将任何一棵树分为两个部分：

1.左路节点

2.左路节点的右子树

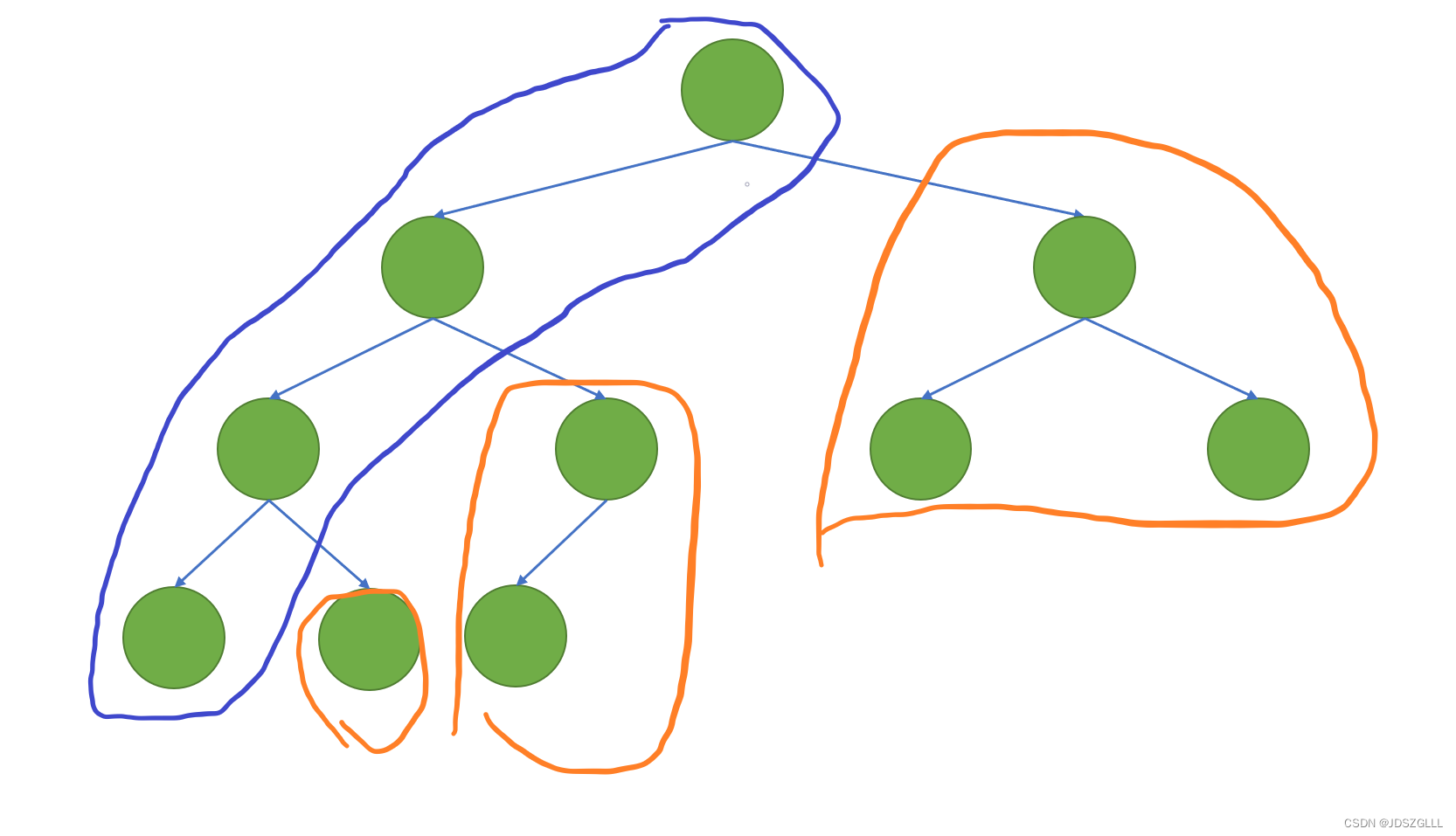
前序

//前序
class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        TreeNode* cur = root;
        vector<int> v;
        stack<TreeNode*> s;
        while (cur || !s.empty())
        {
            while (cur)
            {
                s.push(cur);
                v.push_back(cur->val);
                cur = cur->left;
            }

            TreeNode* top = s.top();
            s.pop();
            cur = top->right;
        }
        return v;

    }
};

中序

//中序
class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> ret;
        stack<TreeNode*> st;
        TreeNode* cur = root;

        while (cur || !st.empty())
        {
            while (cur)
            {
                st.push(cur);
                cur = cur->left;
            }

            TreeNode* top = st.top();

            st.pop();
            ret.push_back(top->val);

            cur = top->right;
        }
        return ret;
    }
};

后序

//后序

class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        vector<int> v;
        stack<TreeNode*> st;
        TreeNode* cur = root;
        TreeNode* pre = nullptr;

        while (cur || !st.empty())
        {
            while (cur)
            {
                st.push(cur);
                cur = cur->left;
            }

            TreeNode* top = st.top();

            if (top->right == nullptr || top->right == pre)
            {
                st.pop();
                v.push_back(top->val);
                pre = top;
            }
            else
            {
                cur = top->right;
            }

        }
        return v;

    }
};