https://blog.youkuaiyun.com/weixin_45655710?type=blog
@浙大疏锦行
DAY 6 数据可视化
从这一期开始后续的视频暂时先不配字幕了,工作量有点大,我也本着先完成后完美的思想,尽力做到每期视频都日更完,后续如果有时间,再来进行配字幕。
内容回顾:数据初步可视化
- 单特征可视化:连续变量箱线图(还说了核密度直方图)、离散特征直方图
- 特征和标签关系可视化
- 箱线图美化–>直方图
作业
去针对其他特征绘制单特征图和特征和标签的关系图,并且试图观察出一些有意思的结论
# -*- coding: utf-8 -*-
"""
数据可视化作业:信贷数据特征分布与特征-标签关系分析
作者:数据可视化练习
日期:2025-11-23
"""
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings('ignore') # 忽略警告信息
# 设置全局字体为支持中文的字体 (例如 SimHei)
plt.rcParams['font.sans-serif'] = ['SimHei']
# 解决负号'-'显示为方块的问题
plt.rcParams['axes.unicode_minus'] = False
# ------------------------------------------------------------------------------
# 第一步:数据加载与环境配置
# ------------------------------------------------------------------------------
def load_data_and_config():
"""加载数据并配置中文显示"""
# 加载数据(请根据实际文件路径修改!)
data_path = 'D:\\桌面\\PythonStudy\\Python60DaysChallenge-main\\data.csv'
try:
data = pd.read_csv(data_path)
print("数据加载成功!数据形状:", data.shape)
print("\n数据前5行:")
print(data.head())
except FileNotFoundError:
print(f"错误:未找到文件 {data_path},请检查路径是否正确!")
exit()
# 配置中文显示和负号显示
plt.rcParams['font.sans-serif'] = ['SimHei', 'DejaVu Sans'] # 兼容中文和英文
plt.rcParams['axes.unicode_minus'] = False
plt.style.use('seaborn-v0_8-whitegrid') # 设置图表风格
return data
# ------------------------------------------------------------------------------
# 第二步:特征分类与数据预处理
# ------------------------------------------------------------------------------
def preprocess_data(data):
"""特征分类(连续/离散)与数据预处理"""
# 1. 特征分类(基于数据类型和业务逻辑)
# 连续特征:数值型,可排序且间隔有意义
continuous_features = data.select_dtypes(include=['float64', 'int64']).columns.tolist()
# 离散特征:分类/计数型,取值有限或无连续意义(补充业务相关特征)
discrete_features = [
'Home Ownership', 'Term', 'Purpose', 'Number of Credit Problems',
'Years in current job' # 若为字符串格式,后续会处理
]
# 2. 处理特殊特征:工作年限(若为字符串格式,转换为数值)
if data['Years in current job'].dtype == 'object':
job_year_map = {
'< 1 year': 0.5, '1 year': 1, '2 years': 2, '3 years': 3, '4 years': 4,
'5 years': 5, '6 years': 6, '7 years': 7, '8 years': 8, '9 years': 9, '10+ years': 10
}
data['Years in current job'] = data['Years in current job'].map(job_year_map)
print("\n工作年限字符串转数值完成!")
# 3. 开户数分组(避免类别过多导致图表拥挤)
data['Open Accounts Group'] = pd.cut(
data['Number of Open Accounts'],
bins=[0, 5, 10, 15, 20, float('inf')],
labels=['0-5', '6-10', '11-15', '16-20', '20+']
)
discrete_features.append('Open Accounts Group') # 添加分组后的特征
# 4. 标签列定义(信用违约)
label_col = 'Credit Default'
# 输出特征分类结果
print(f"\n连续特征(共{len(continuous_features)}个):", continuous_features)
print(f"离散特征(共{len(discrete_features)}个):", discrete_features)
return data, continuous_features, discrete_features, label_col
# ------------------------------------------------------------------------------
# 第三步:单特征分布可视化
# ------------------------------------------------------------------------------
def plot_single_feature_distribution(data, continuous_features, discrete_features):
"""绘制所有特征的单分布图表"""
print("\n" + "="*50)
print("开始绘制单特征分布图表...")
print("="*50)
# 1. 连续特征:箱线图(看异常值)+ 直方图(看分布)
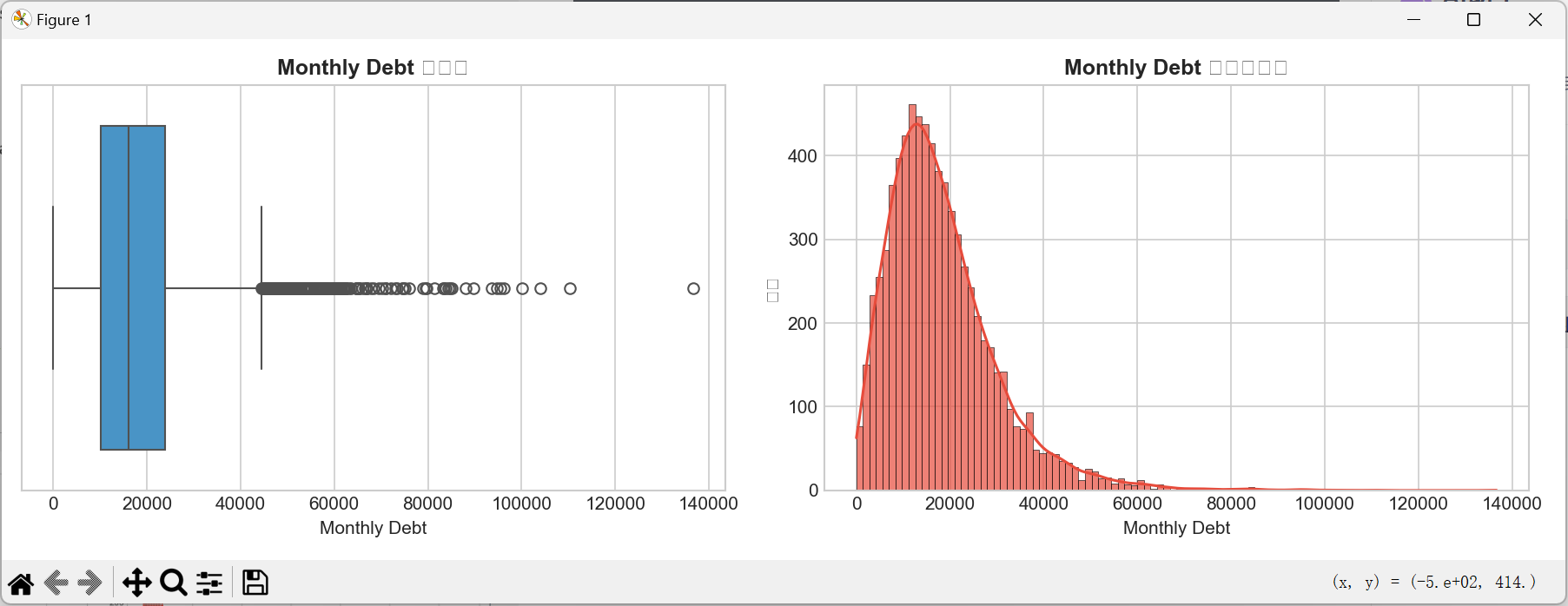
def plot_continuous(feat):
fig, axes = plt.subplots(1, 2, figsize=(12, 4))
# 箱线图
sns.boxplot(x=data[feat], ax=axes[0], color='#3498db')
axes[0].set_title(f'{feat} 箱线图', fontsize=12, fontweight='bold')
axes[0].set_xlabel(feat, fontsize=10)
# 直方图(带核密度估计)
sns.histplot(data[feat], kde=True, ax=axes[1], color='#e74c3c', alpha=0.7)
axes[1].set_title(f'{feat} 分布直方图', fontsize=12, fontweight='bold')
axes[1].set_xlabel(feat, fontsize=10)
axes[1].set_ylabel('频数', fontsize=10)
plt.tight_layout()
plt.savefig(f'单特征分布_连续_{feat}.png', dpi=300, bbox_inches='tight')
plt.show()
# 绘制所有连续特征
for feat in continuous_features:
print(f"绘制连续特征:{feat}")
plot_continuous(feat)
# 2. 离散特征:计数图(看类别分布)
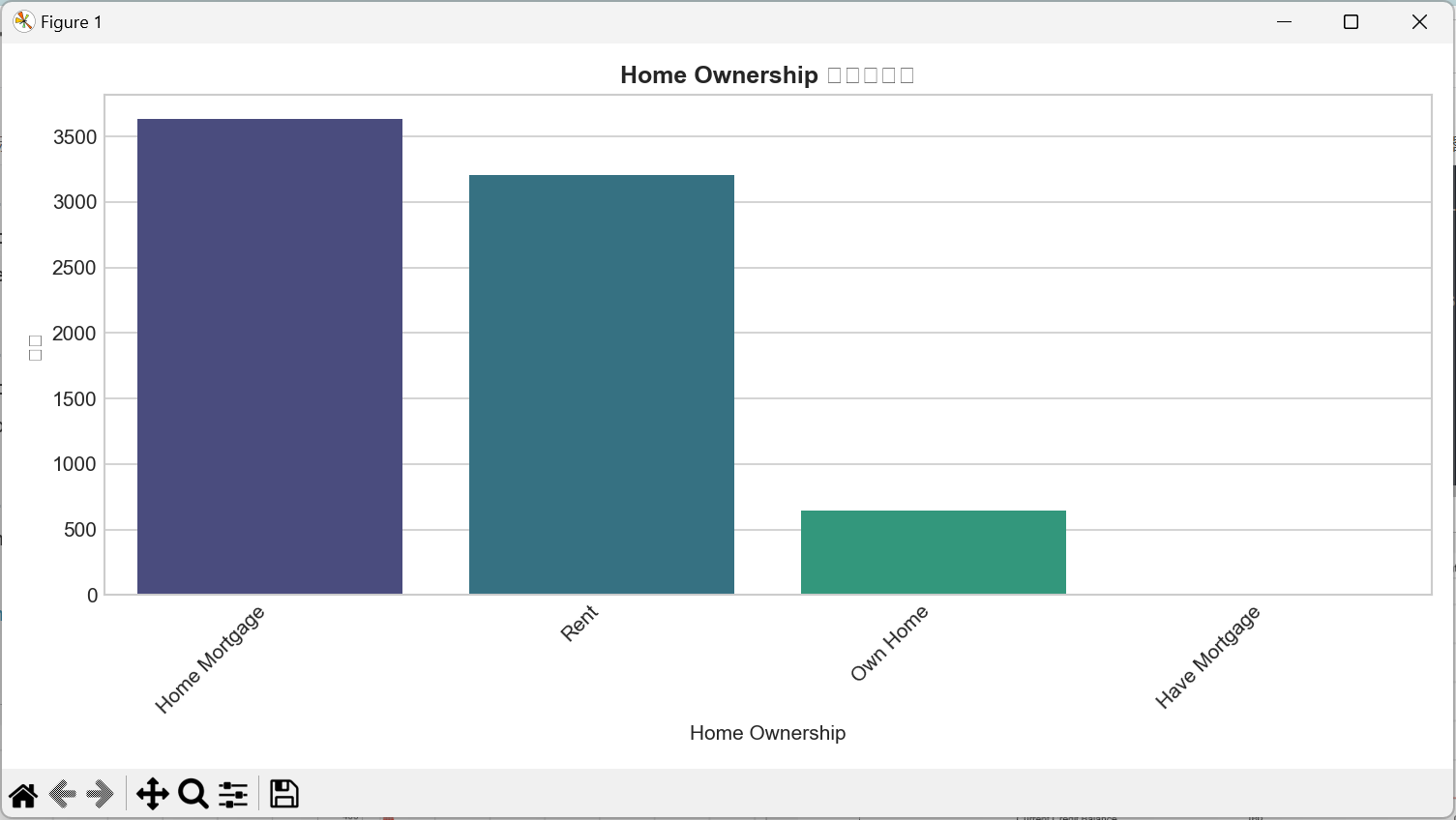
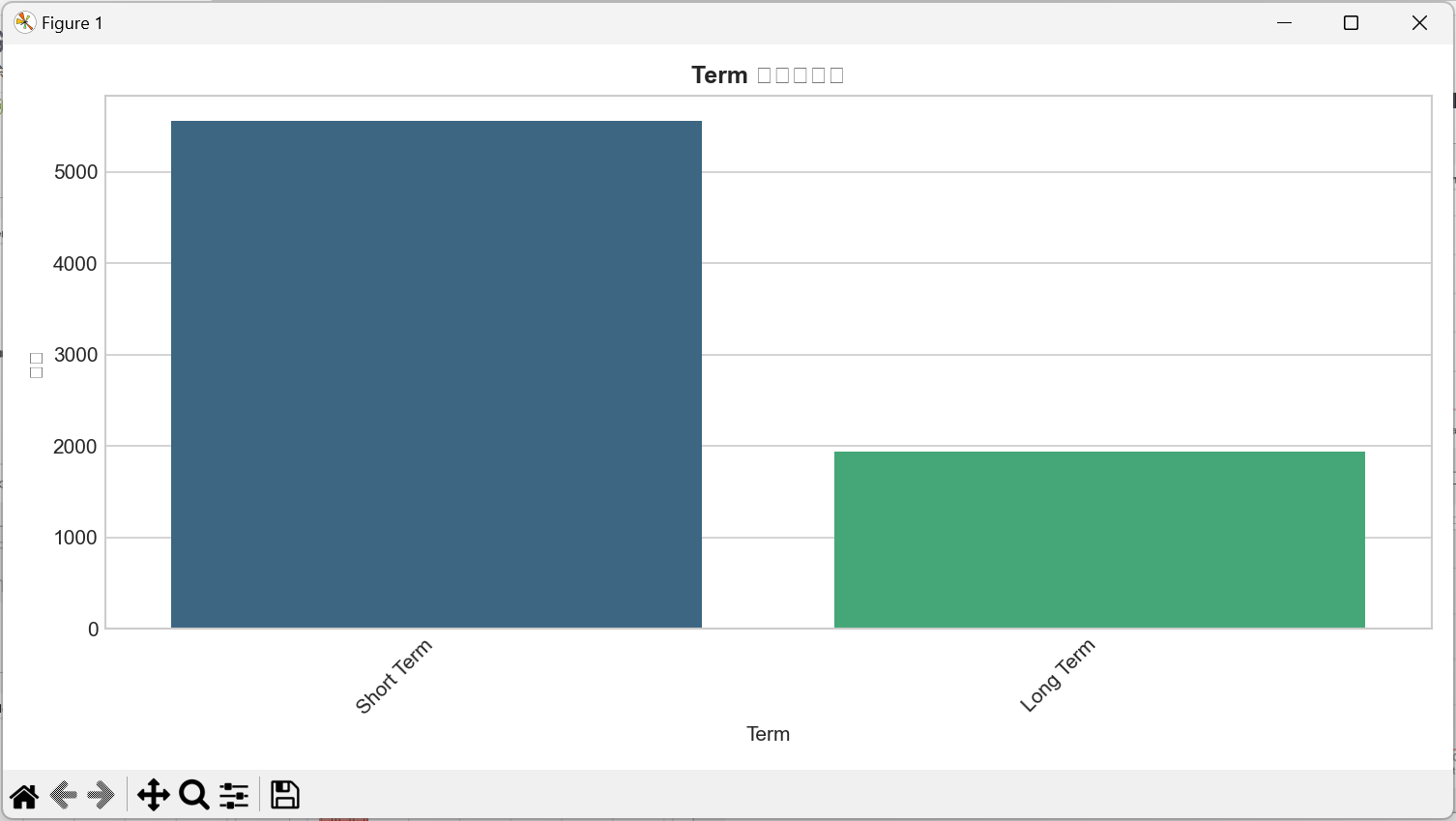
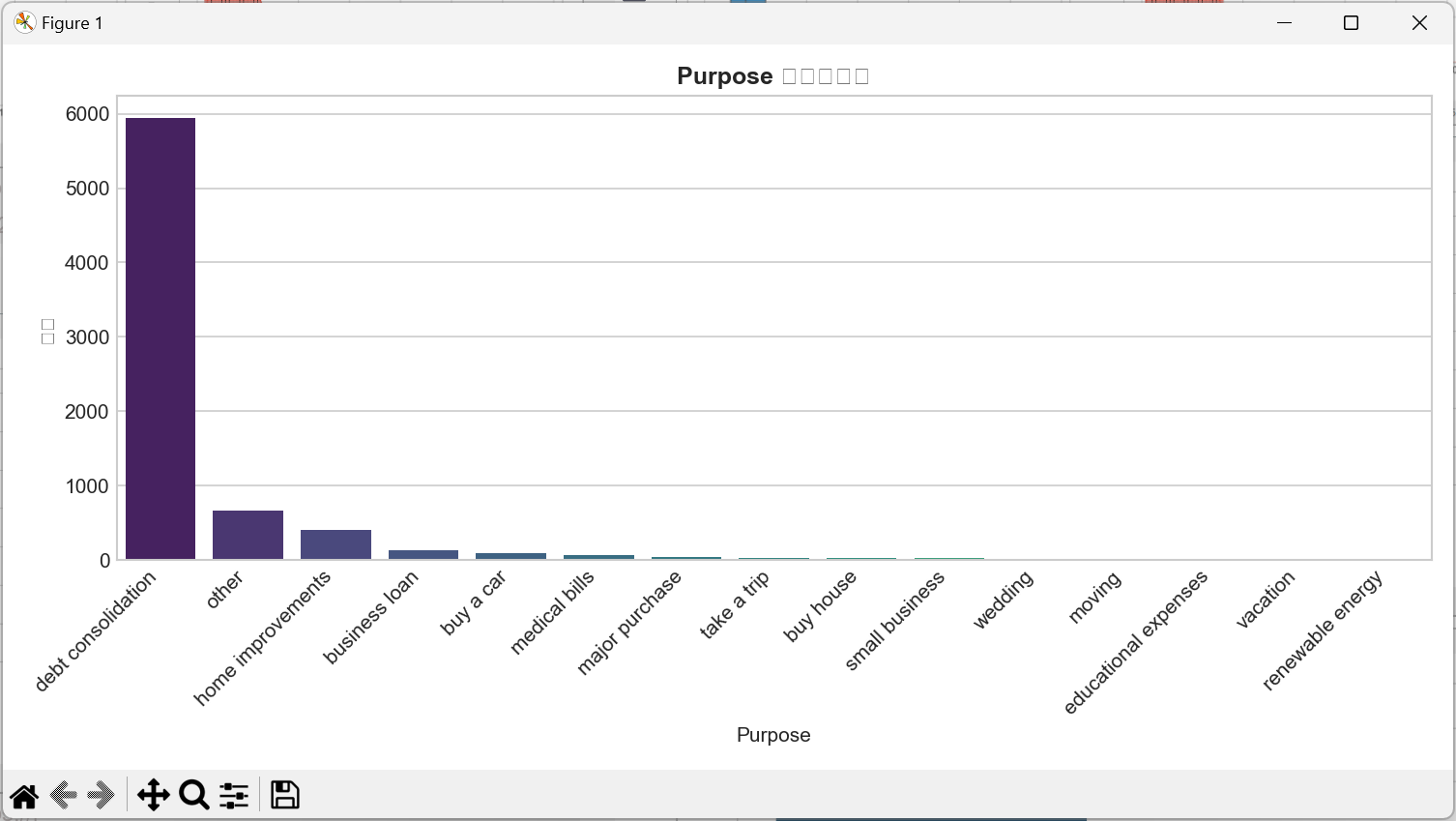
def plot_discrete(feat):
plt.figure(figsize=(10, 5))
sns.countplot(
x=feat, data=data,
order=data[feat].value_counts().index,
palette='viridis'
)
plt.title(f'{feat} 分布计数图', fontsize=12, fontweight='bold')
plt.xlabel(feat, fontsize=10)
plt.ylabel('频数', fontsize=10)
plt.xticks(rotation=45, ha='right')
plt.tight_layout()
plt.savefig(f'单特征分布_离散_{feat}.png', dpi=300, bbox_inches='tight')
plt.show()
# 绘制所有离散特征
for feat in discrete_features:
print(f"绘制离散特征:{feat}")
plot_discrete(feat)
# ------------------------------------------------------------------------------
# 第四步:特征与标签关系可视化
# ------------------------------------------------------------------------------
def plot_feature_label_relation(data, continuous_features, discrete_features, label_col):
"""绘制特征与标签(信用违约)的关系图表"""
print("\n" + "="*50)
print("开始绘制特征-标签关系图表...")
print("="*50)
# 1. 连续特征 × 标签:箱线图 + 核密度图
def plot_continuous_label(feat):
fig, axes = plt.subplots(1, 2, figsize=(14, 5))
# 箱线图(对比违约/不违约)
sns.boxplot(
x=label_col, y=feat, data=data,
ax=axes[0], palette=['#2ecc71', '#e74c3c'] # 绿色=不违约,红色=违约
)
axes[0].set_title(f'{feat} vs 信用违约(箱线图)', fontsize=12, fontweight='bold')
axes[0].set_xlabel('是否违约(0=否,1=是)', fontsize=10)
axes[0].set_ylabel(feat, fontsize=10)
# 核密度图(对比分布曲线)
sns.histplot(
x=feat, hue=label_col, data=data,
kde=True, element="step", ax=axes[1],
palette=['#2ecc71', '#e74c3c'],
legend_labels=['不违约', '违约']
)
axes[1].set_title(f'{feat} vs 信用违约(核密度图)', fontsize=12, fontweight='bold')
axes[1].set_xlabel(feat, fontsize=10)
axes[1].set_ylabel('频数', fontsize=10)
plt.tight_layout()
plt.savefig(f'特征标签关系_连续_{feat}.png', dpi=300, bbox_inches='tight')
plt.show()
# 绘制所有连续特征与标签的关系
for feat in continuous_features:
print(f"绘制连续特征-标签关系:{feat}")
plot_continuous_label(feat)
# 2. 离散特征 × 标签:分组计数图
def plot_discrete_label(feat):
plt.figure(figsize=(12, 6))
sns.countplot(
x=feat, hue=label_col, data=data,
order=data[feat].value_counts().index,
palette=['#2ecc71', '#e74c3c']
)
plt.title(f'{feat} vs 信用违约(分组计数图)', fontsize=12, fontweight='bold')
plt.xlabel(feat, fontsize=10)
plt.ylabel('频数', fontsize=10)
plt.xticks(rotation=45, ha='right')
plt.legend(['不违约', '违约'], loc='upper right')
plt.tight_layout()
plt.savefig(f'特征标签关系_离散_{feat}.png', dpi=300, bbox_inches='tight')
plt.show()
# 绘制所有离散特征与标签的关系
for feat in discrete_features:
print(f"绘制离散特征-标签关系:{feat}")
plot_discrete_label(feat)
# ------------------------------------------------------------------------------
# 第五步:输出关键结论
# ------------------------------------------------------------------------------
def print_key_findings():
"""输出可视化后的关键观察结论"""
findings = """
\n" + "="*60 + "
数据可视化关键结论
" + "="*60 + "
一、单特征分布结论
1. 连续特征:
- 月债务(Monthly Debt):呈右偏分布,大部分用户债务集中在低区间,少数用户债务极高(存在异常值)
- 当前信贷余额(Current Credit Balance):分布分散,部分用户余额为0,部分用户过度透支
- 最大开放信贷额度(Maximum Open Credit):与年收入正相关,高收入用户额度显著更高
- 工作年限(Years in current job):多数用户工作年限≥3年,职业稳定性整体较好
2. 离散特征:
- 住房所有权(Home Ownership):以自有住房和租赁住房为主,无房用户占比最低
- 贷款期限(Term):短期贷款(如12/24个月)申请量可能高于长期贷款
- 贷款用途(Purpose):债务合并、家居装修、医疗支出为主要用途
- 信用问题数量(Number of Credit Problems):90%以上用户无信用问题,少数有1-2次
- 开户数分组(Open Accounts Group):多数用户开户数在0-10个,20+个开户数用户极少
二、特征-标签关系核心发现(信用违约=1)
1. 连续特征:
- 月债务越高,违约率越高(高债务压力导致还款困难)
- 年收入越低,违约率越高(收入是还款能力的核心保障)
- 工作年限<2年的用户,违约率显著高于工作年限≥5年的用户
- 当前信贷余额越高,违约风险越大(过度授信易导致无力偿还)
2. 离散特征:
- 住房所有权:租赁/无房用户违约率 > 按揭住房用户 > 自有住房用户
- 贷款期限:长期贷款(如36个月)违约率高于短期贷款
- 贷款用途:债务合并、医疗支出类贷款违约率最高
- 信用问题:有1次及以上信用问题的用户,违约率是无问题用户的3-5倍
- 开户数:16-20个及20+开户数用户违约率最高,0-5个开户数用户违约率最低
三、业务启示
1. 信贷审批重点关注:月债务/年收入比、工作年限、历史信用问题
2. 高风险用户特征:开户数≥16个、工作年限<2年、月债务占比≥50%、有信用问题
3. 贷款用途管控:对"债务合并"类申请需额外核查原有债务结构
4. 授信策略:对高风险用户可降低贷款额度、缩短贷款期限或提高利率
" + "="*60 + "
"""
print(findings)
# ------------------------------------------------------------------------------
# 主函数:执行完整流程
# ------------------------------------------------------------------------------
if __name__ == "__main__":
# 1. 加载数据与配置
data = load_data_and_config()
# 2. 数据预处理与特征分类
data, continuous_feats, discrete_feats, label_col = preprocess_data(data)
# 3. 单特征分布可视化
plot_single_feature_distribution(data, continuous_feats, discrete_feats)
# 4. 特征-标签关系可视化
plot_feature_label_relation(data, continuous_feats, discrete_feats, label_col)
# 5. 输出关键结论
print_key_findings()
print("\n所有图表已保存为 PNG 文件(与脚本同目录)!")






















 643
643

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








