排序算法汇总

排序算法汇总和实现

这一篇博文汇总了十种排序算法，每种排序算法都有各自的优点与不足，因此使用场景也不一样。从使用频率来看，快速排序使用的最多，这是因为快速排序的思路非常巧妙，并且易于理解，最关键的是效果一般情况下都不错，在讲解中，快速排序也将作为最重要的内容。

先对比下十种排序算法的时间复杂度，空间复杂度等，直接上图
，该图说明了每种排序算法的平均时间复杂度，最好以及最坏时间复杂度，空间复杂度以及稳定性。
可参考(https://blog.youkuaiyun.com/qq_38400583/article/details/95594589)

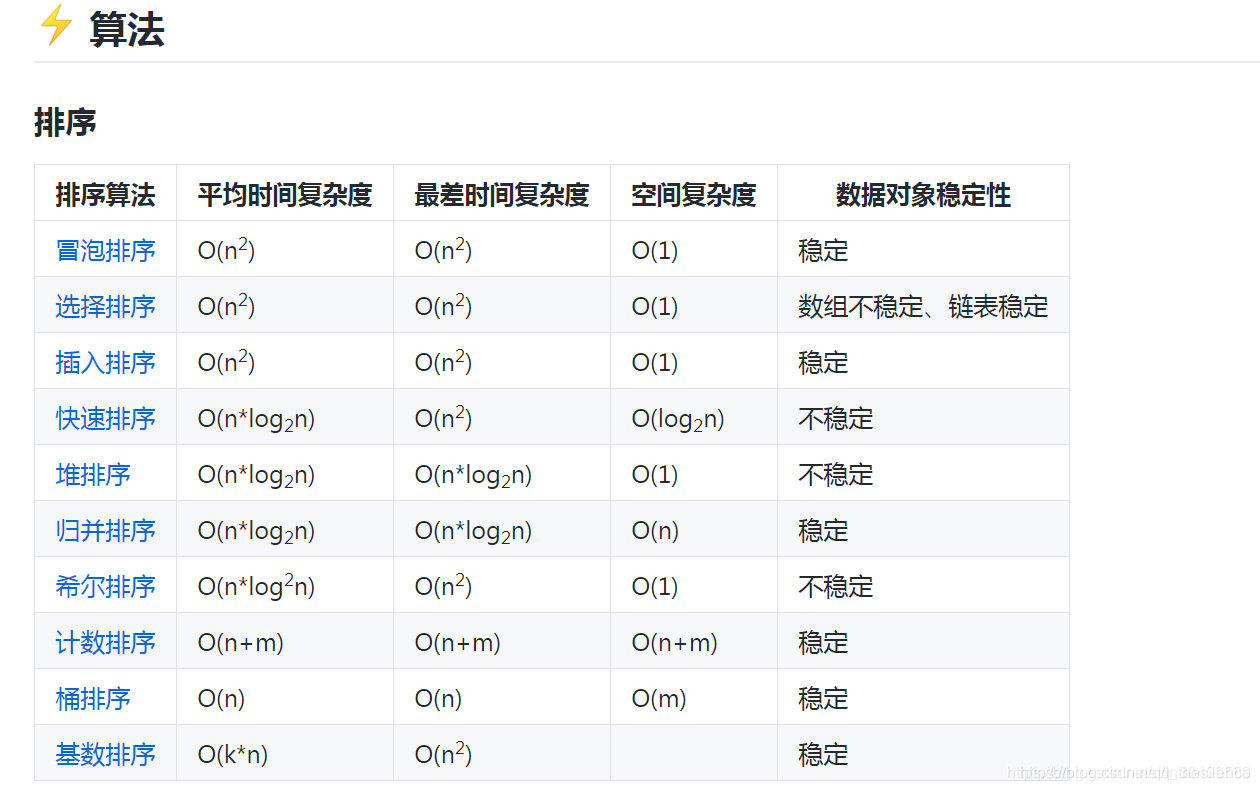
算法稳定性

排序算法的稳定性是指数组里面相同元素的相对位置在排序前后不发生改变，这是一种衡量指标，表明算法在执行过程中对于原数组相同元素的处理能力。这也是面试时面试官喜欢问的排序问题之一。

冒泡排序

冒泡排序（Bubble sort）是一种简单的排序算法。它重复地走访过要排序的数列，一次比较两个元素，如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行指导没有再进行交换，也就是说数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。
　　算法原理：
　　(1) 比较相邻的元素。如果第一个比第二个大，就交换他们两个；
　　(2) 对每一个相邻元素作同样的工作，从开始第一对到结尾的最后一对。在这一点，最后的元素 　　　应该会是最大的数；
　　(3) 针对所有的元素重复以上的步骤，除了最后一个；
　　(4) 持续每次对越来越小的元素重复上面的步骤，直到没有任何一对数字需要比较。

```cpp
void swap(int *p, int *q)
{
	int t = *p;
	*p = *q;
	*q = t;
}


void bubbleSort(int *a, int n)
{
	for (int i = 0; i < n－1； i++)
	{
		for (int j = 0; j < n - 1 - i; j++)
		{
			if (a[j] > a[j + 1])
			{
				swap(&a[j], &a[j + 1]);
			}
		}
	}
}		

改进：冒泡排序是一个稳定的算法，在遇到相同的元素时并不交换位置。该算法可以在上面的代码中进行优化，因为如果数组有序的话，交换行为就不会发生。因此可以对交换行为进行状态标记，若发现一趟循环下来没有发生交换行为，便可以退出。

选择排序

选择排序（Selection sort）是一种简单直观的排序算法。它的工作原理是每一趟从待排序的数据元素中选出最小（或最大）的一个元素，顺序放在已经排好序的数列的最后，直到全部待排序的数据元素排完。因此，每一遍历数组时其遍历范围都会减小。该算法不稳定，因为找到目标值后直接与最后的位置交换，这可能导致相同元素的位置发生改变

void selectSort(int *a, int n)
{
	int min = 0;
	for (int i = 0; i < n - 1; i++) {
		min = i;//假设最小值的下标为i
		for (int j = i + 1; j < n; j++)
		{
			//在min位置的数与后面的数比较找出最小值下标
			if (a[min] > a[j])
			{
				min = j;
			}
		}
		//最小值与无序的第一个数交换
		if (min != i)
		{
			int t = a[i];
			a[i] = a[min];
			a[min] = t;
		}
	}
}

插入排序

插入排序的过程是这样：每次从原先的数组起始位置拿一个数，这个数和另一个数组作插入操作，其过程是从另一数组右边往左边遍历，比较每次从原先数组拿的数和另一数组遍历位置元素的大小，如果发现某个位置比原数组元素小，就将原数组元素插入到其后面，而后面的元素位置都要后移一位。这个过程最形象的比喻就是扑克牌抽取，大家感兴趣可以搜一下。插入排序很容易理解，就是每次拿一个数一个一个比较，对于有序数组，该算法非常有效。

插入排序思路：
1.从第一个元素开始，该元素可以认为已经被排序
2.取出下一个元素，在已经排序的元素序列中从后向前扫描
3.如果该元素（已排序）大于新元素，将该元素移到下一位置
4.重复步骤3，直到找到已排序的元素小于或者等于新元素的位置
5.将新元素插入到该位置后
6.重复步骤2~5

void InsertSort(vector<int>& v)
{
    int len = v.size();
	for (int i = 1; i < len; ++i) {
		int temp = v[i];
        for(int j = i - 1; j >= 0; --j)
        {
            if(v[j] > temp)
            {
                v[j + 1] = v[j];
                v[j] = temp;
            }
            else
                break;
        }
	}
}

快速排序（QuickSort）

先说下快速排序的思想：从原始数组选取一个数，将数组中小于该数的所有数值放在其左边，大于该数的值都放在其右边，这样第一趟下来，其实排序后的数组中间的元素已经确定好了。剩下的就是对刚刚第一趟结果数组左边的所有数和右边的所有数分别递归该过程，即可得到排序结果。听起来过程很简单，只需要将数组划分下即可。这也是该算法的特点，容易实现，易于理解。但是前提是使用者要对递归熟悉。该算法之所以快是因为每趟下来中间的数都已经在最终的位置上了。但该算法并不稳定，由于每次划分的随机性，相同元素的位置不能保证不发生改变。

快速排序思路：
1.选取第一个数为基准
2.将比基准小的数交换到前面，比基准大的数交换到后面
3.对左右区间重复第二步，直到各区间只有一个数

void QuickSort(vector<int>& v, int low, int high) {
	if (low >= high)		// 结束标志
		return;
	int first = low;		// 低位下标
	int last = high;		// 高位下标
	int key = v[first];		// 设第一个为基准

	while (first < last)
	{
		// 将比第一个小的移到前面
		while (first < last && v[last] >= key)
			last--;
		if (first < last)
			v[first++] = v[last];

		// 将比第一个大的移到后面
		while (first < last && v[first] <= key)
			first++;
		if (first < last)
			v[last--] = v[first];
	}
	// 基准置位
	v[first] = key;
	// 前半递归
	QuickSort(v, low, first - 1);
	// 后半递归
	QuickSort(v, first + 1, high);
}

上述快排算法是每次选取最左端的值作为划分基准，是一种很常用的方法，容易理解。但也有另外的方法可以实现，一种可行的思路如下：
1.每次选取最右端的值作为基准
2.设置一个指针，用来记录已经排序好的位置，初始值为-1，没有位置排序
3.从最左边开始遍历，遇到大于基准的元素跳过，如果遇到小于基准的元素时，将其与记录指针后面的一个位置交换值，同时记录指针加一
4.重复3步骤

堆排序

堆排序（大顶堆）：用到了堆这种数据结构，其本质上是一个二叉树，只不过大的元素在上面，小的元素在下面，小顶堆相反。利用该结构排序当然要用到递归，因此才能有nlogn的复杂度。其过程如下：
1.将原数组构建为大顶堆
2.交换堆顶元素与最后一个节点的元素交换，这样最大的元素就到最后的位置了
3.重复上述步骤

void max_heapify(int arr[], int start, int end) {
	//建立父節點指標和子節點指標
	int dad = start;
	int son = dad * 2 + 1;
	while (son <= end) { //若子節點指標在範圍內才做比較
		if (son + 1 <= end && arr[son] < arr[son + 1]) //先比較兩個子節點大小，選擇最大的
			son++;
		if (arr[dad] > arr[son]) //如果父節點大於子節點代表調整完畢，直接跳出函數
			return;
		else { //否則交換父子內容再繼續子節點和孫節點比較
			swap(arr[dad], arr[son]);
			dad = son;
			son = dad * 2 + 1;
		}
	}
}

void heap_sort(int arr[], int len) {
	//初始化，i從最後一個父節點開始調整
	for (int i = len / 2 - 1; i >= 0; i--)
		max_heapify(arr, i, len - 1);
	//先將第一個元素和已经排好的元素前一位做交換，再從新調整(刚调整的元素之前的元素)，直到排序完畢
	for (int i = len - 1; i > 0; i--) {
		swap(arr[0], arr[i]);
		max_heapify(arr, 0, i - 1);
	}
}

归并排序

归并排序：把数据分为两段，从两段中逐个选最小的元素移入新数据段的末尾。可从上到下或从下到上进行。

template<typename T>
void merge_sort_recursive(T arr[], T reg[], int start, int end) {
	if (start >= end)
		return;
	int len = end - start, mid = (len >> 1) + start;
	int start1 = start, end1 = mid;
	int start2 = mid + 1, end2 = end;
	merge_sort_recursive(arr, reg, start1, end1);
	merge_sort_recursive(arr, reg, start2, end2);
	int k = start;
	while (start1 <= end1 && start2 <= end2)
		reg[k++] = arr[start1] < arr[start2] ? arr[start1++] : arr[start2++];
	while (start1 <= end1)
		reg[k++] = arr[start1++];
	while (start2 <= end2)
		reg[k++] = arr[start2++];
	for (k = start; k <= end; k++)
		arr[k] = reg[k];
}
//整數或浮點數皆可使用,若要使用物件(class)時必須設定"小於"(<)的運算子功能
template<typename T> 
void merge_sort(T arr[], const int len) {
	T *reg = new T[len];
	merge_sort_recursive(arr, reg, 0, len - 1);
	delete[] reg;
}

希尔排序

每一轮按照事先决定的间隔进行插入排序，间隔会依次缩小，最后一次一定要是1。

template<typename T>
void shell_sort(T array[], int length) {
    int h = 1;
    while (h < length / 3) {
        h = 3 * h + 1;
    }
    while (h >= 1) {
        for (int i = h; i < length; i++) {
            for (int j = i; j >= h && array[j] < array[j - h]; j -= h) {
                std::swap(array[j], array[j - h]);
            }
        }
        h = h / 3;
    }
}

计数排序

计数排序：统计小于等于该元素值的元素的个数i，于是该元素就放在目标数组的索引i位（i≥0）。
计数排序基于一个假设，待排序数列的所有数均为整数，且出现在（0，k）的区间之内。
如果 k（待排数组的最大值） 过大则会引起较大的空间复杂度，一般是用来排序 0 到 100 之间的数字的最好的算法，但是它不适合按字母顺序排序人名。
计数排序不是比较排序，排序的速度快于任何比较排序算法。
时间复杂度为 O（n+k），空间复杂度为 O（n+k）
算法的步骤如下：

1.找出待排序的数组中最大和最小的元素
2.统计数组中每个值为 i 的元素出现的次数，存入数组 C 的第 i 项
3.对所有的计数累加（从 C 中的第一个元素开始，每一项和前一项相加）
4.反向填充目标数组：将每个元素 i 放在新数组的第 C[i] 项，每放一个元素就将 C[i] 减去 1

void CountSort(vector<int>& vecRaw, vector<int>& vecObj)
{
	// 确保待排序容器非空
	if (vecRaw.size() == 0)
		return;

	// 使用 vecRaw 的最大值 + 1 作为计数容器 countVec 的大小
	int vecCountLength = (*max_element(begin(vecRaw), end(vecRaw))) + 1;
	vector<int> vecCount(vecCountLength, 0);

	// 统计每个键值出现的次数
	for (int i = 0; i < vecRaw.size(); i++)
		vecCount[vecRaw[i]]++;
	
	// 后面的键值出现的位置为前面所有键值出现的次数之和
	for (int i = 1; i < vecCountLength; i++)
		vecCount[i] += vecCount[i - 1];

	// 将键值放到目标位置
	for (int i = vecRaw.size(); i > 0; i--)	// 此处逆序是为了保持相同键值的稳定性
		vecObj[--vecCount[vecRaw[i - 1]]] = vecRaw[i - 1];
}

桶排序

桶排序：将值为i的元素放入i号桶，最后依次把桶里的元素倒出来。
桶排序序思路：

1.设置一个定量的数组当作空桶子。
2.寻访序列，并且把项目一个一个放到对应的桶子去。
3.对每个不是空的桶子进行排序。
4.从不是空的桶子里把项目再放回原来的序列中。
5.假设数据分布在[0，100)之间，每个桶内部用链表表示，在数据入桶的同时插入排序，然后把各个桶中的数据合并。

#include<iterator>
#include<iostream>
#include<vector>
using std::vector;

const int BUCKET_NUM = 10;

struct ListNode{
	explicit ListNode(int i=0):mData(i),mNext(NULL){}
	ListNode* mNext;
	int mData;
};

ListNode* insert(ListNode* head,int val){
	ListNode dummyNode;
	ListNode *newNode = new ListNode(val);
	ListNode *pre,*curr;
	dummyNode.mNext = head;
	pre = &dummyNode;
	curr = head;
	while(NULL!=curr && curr->mData<=val){
		pre = curr;
		curr = curr->mNext;
	}
	newNode->mNext = curr;
	pre->mNext = newNode;
	return dummyNode.mNext;
}


ListNode* Merge(ListNode *head1,ListNode *head2){
	ListNode dummyNode;
	ListNode *dummy = &dummyNode;
	while(NULL!=head1 && NULL!=head2){
		if(head1->mData <= head2->mData){
			dummy->mNext = head1;
			head1 = head1->mNext;
		}else{
			dummy->mNext = head2;
			head2 = head2->mNext;
		}
		dummy = dummy->mNext;
	}
	if(NULL!=head1) dummy->mNext = head1;
	if(NULL!=head2) dummy->mNext = head2;
	
	return dummyNode.mNext;
}

void BucketSort(int n,int arr[]){
	vector<ListNode*> buckets(BUCKET_NUM,(ListNode*)(0));
	for(int i=0;i<n;++i){
		int index = arr[i]/BUCKET_NUM;
		ListNode *head = buckets.at(index);
		buckets.at(index) = insert(head,arr[i]);
	}
	ListNode *head = buckets.at(0);
	for(int i=1;i<BUCKET_NUM;++i){
		head = Merge(head,buckets.at(i));
	}
	for(int i=0;i<n;++i){
		arr[i] = head->mData;
		head = head->mNext;
	}
}

基数排序

基数排序：一种多关键字的排序算法，可用桶排序实现。

int maxbit(int data[], int n) //辅助函数，求数据的最大位数
{
    int maxData = data[0];		///< 最大数
    /// 先求出最大数，再求其位数，这样有原先依次每个数判断其位数，稍微优化点。
    for (int i = 1; i < n; ++i)
    {
        if (maxData < data[i])
            maxData = data[i];
    }
    int d = 1;
    int p = 10;
    while (maxData >= p)
    {
        //p *= 10; // Maybe overflow
        maxData /= 10;
        ++d;
    }
    return d;
/*    int d = 1; //保存最大的位数
    int p = 10;
    for(int i = 0; i < n; ++i)
    {
        while(data[i] >= p)
        {
            p *= 10;
            ++d;
        }
    }
    return d;*/
}
void radixsort(int data[], int n) //基数排序
{
    int d = maxbit(data, n);
    int *tmp = new int[n];
    int *count = new int[10]; //计数器
    int i, j, k;
    int radix = 1;
    for(i = 1; i <= d; i++) //进行d次排序
    {
        for(j = 0; j < 10; j++)
            count[j] = 0; //每次分配前清空计数器
        for(j = 0; j < n; j++)
        {
            k = (data[j] / radix) % 10; //统计每个桶中的记录数
            count[k]++;
        }
        for(j = 1; j < 10; j++)
            count[j] = count[j - 1] + count[j]; //将tmp中的位置依次分配给每个桶
        for(j = n - 1; j >= 0; j--) //将所有桶中记录依次收集到tmp中
        {
            k = (data[j] / radix) % 10;
            tmp[count[k] - 1] = data[j];
            count[k]--;
        }
        for(j = 0; j < n; j++) //将临时数组的内容复制到data中
            data[j] = tmp[j];
        radix = radix * 10;
    }
    delete []tmp;
    delete []count;
}