数据结构-排序-快排

快排

算法思想
单趟排序：选出一个KEY，一般是最左边的或者是最右边的，把KEY放到他正确的位置上去，左边的比KEY小，右边的比KEY大。左边的值做KEY，则右边的先走。

三数取中

//三数取中，可以优化有序数列的情况。但当其元素都相等的时候，就无法进行优化。
int GetMidIndex(int *a, int left, int right)
{
	int mid = (left + right) >> 1;
	if (a[left] < a[mid])
	{
		if (a[mid] < a[right])
		{
			return mid;
		}
		else if (a[left]>a[right])
		{
			return left;
		}
		else
		{
			return right;
		}

	}
	else
	{
		if (a[mid] > a[right])
		{
			return mid;
		}
		else if (a[left] < a[right])
		{
			return left;
		}
		else
		{
			return right;
		}
	}
}

hoare–左右指针法

int PartSort1(int * a, int left, int right)
{
	int minIndex = GetMidIndex(a, left, right);
	Swap(&a[left], &a[minIndex]);
	int keyi = left;
	while (left < right)
	{
		//找小
		while (left < right&&a[right] >= a[keyi])
			--right;
		//找大
		while (left < right&& a[left] <= a[keyi])
			++left;
		Swap(&a[right], &a[left]);
	}
	Swap(&a[keyi], &a[left]);
	return left;
}

void QuickSort(int * a, int begin, int end)
{
	if (begin >= end)
		return;
	int keyi = PartSort(a, begin, end);
	QuickSort(a, begin, keyi - 1);
	QuickSort(a, keyi + 1, end);
}

问题思考：
为什么最后相遇位置的值一定比key小呢？

因为如果right先走，那么有两种相遇情况
1、right向左走遇到left
left还没有动，保留上一躺交换的小值，当right遇到left，则一定小于key，交换即可。
2、left向右走遇到right
right先走的，则说明right找到比key小的值停了下来，当left向左走的时候，遇到的值一定比key小，则交换。

挖坑法

int PartSort2(int * a, int left, int right)
{
	int key = a[left];
	while (left < right)
	{
		//找小
		while (left < right && a[right] >= key)
		{
			--right;
		}
		//放到左边的坑位，右边形成新的坑位。
		a[left] = a[right];
		while (left < right && a[left] <= key);
		{
			++left;
		}
		a[right] = a[left];
	}
	a[left] = key;
	return left;
}

前后指针法

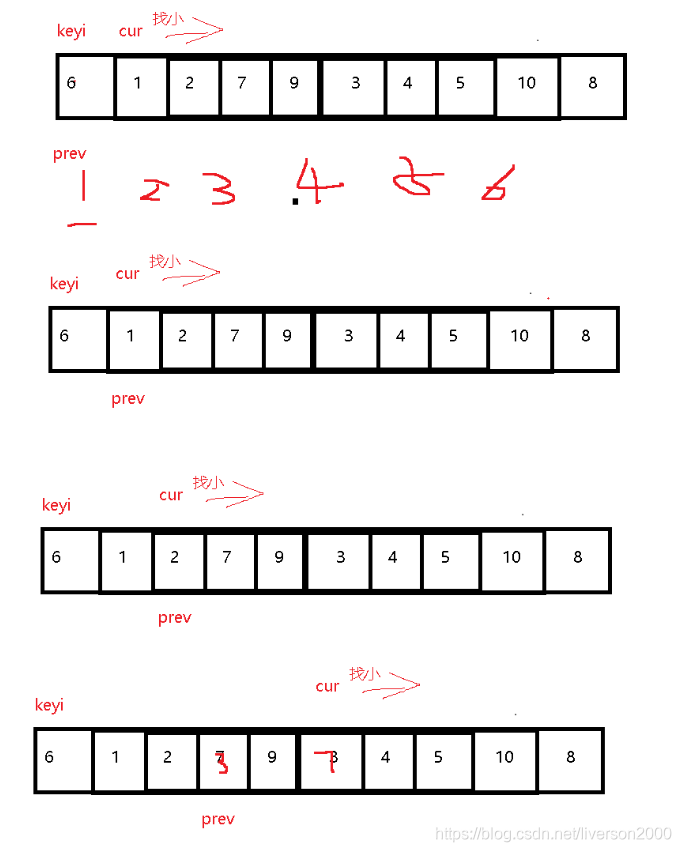
int PartSort3(int * a, int left, int right)
{
	//int keyi =left, prev = left, cur = prev + 1;
	//while (cur <= right)
	//{
	//	//if (cur > right)
	//	//	break;
	//	//while (cur<right && a[cur] >= a[keyi])//找小
	//	//{
	//	//	++cur;
	//	//}
	//	if (a[cur] < a[keyi] && ++prev != cur)
	//	{
	//		Swap(&a[cur], &a[prev]);
	//	}
	//	++cur;	
	//}
	//Swap(&a[prev], &a[keyi]);
	//return prev;
	int keyi = left;
	int prev = left, cur = left + 1;
	while (cur <= right)
	{
		if (a[cur] < a[keyi] && ++prev != cur)
		{
			Swap(&a[cur], &a[prev]);
		}
		++cur;
	}

	Swap(&a[keyi], &a[prev]);

	return prev;






}

小区间优化

void QuickSort(int * a, int begin, int end)
{
	if (begin >= end)
		return;
	//如果子区间数据较多，继续选择key单趟，分割子区间分治递归
	//如果这个子区间数据较少，不再去分治。
	if (end - begin > 20)
	{
		int keyi = PartSort3(a, begin, end);
		QuickSort(a, begin, keyi - 1);
		QuickSort(a, keyi + 1, end);
	}
	else
	{
		HeapSort(a + begin, end - begin + 1);

	}
	//int keyi = PartSort(a, begin, end);
	//QuickSort(a, begin, keyi - 1);
	//QuickSort(a, keyi + 1, end);
}

void QuickSort(int * a, int begin, int end)
{
	if (begin >= end)
		return;
	int keyi = PartSort(a, begin, end);
	QuickSort(a, begin, keyi - 1);
	QuickSort(a, keyi + 1, end);
}

快排的非递归算法

#include "stack.h"

void QuickSortNonR(int * a, int begin, int end)
{
	Stack st;
	StackInit(&st,100);
	StackPush(&st, begin);
	StackPush(&st, end);
	
	while (!StackEmpty(&st))
	{
		int left, right;
		right = StackTop(&st);
		StackPop(&st);

		left = StackTop(&st);
		StackPop(&st);

		int keyi = PartSort1(a, left, right);
		if (left < keyi - 1)
		{
			StackPush(&st, left);
			StackPush(&st, keyi - 1);

		}
		if (keyi + 1 < right)
		{
			StackPush(&st, keyi + 1);
			StackPush(&st, right);
		}
	}

	StackDestory(&st);


}

复杂度分析
理想情况下：每次取到中间的数与key交换，key越接近中位数越接近二分，效率越高。
为O（N*logN）
最坏情况下：有序或接近有序，每次在一侧相遇，
O（N^2）

针对性优化：
1、三数取中
2、小区间排序优化