特殊矩阵的压缩存储（节约内存空间）

边看网课边记的笔记，比较简单，以后遇到详细的再补充，也欢迎大家评论补充！

特殊矩阵简介

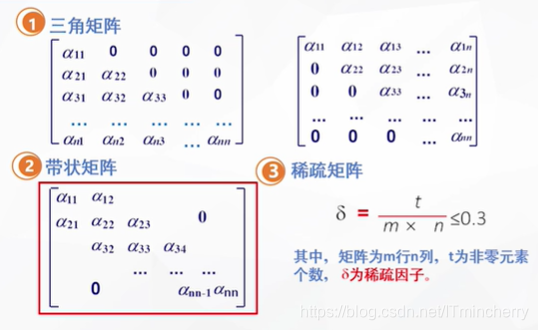
存储方案

三角矩阵和带状矩阵：顺序存储；
稀疏矩阵：（1）三元组顺序表（顺序存储） （2）十字链表（链式存储）（两种方案都不能对矩阵元素进行随机访问）

1. 三角矩阵

三角矩阵分为上三角矩阵和下三角矩阵，只需要存储非零元素。

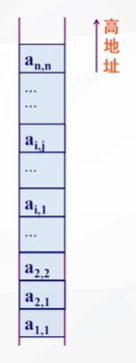
第i行有i个非零元素。于是我们可以得到：
LOC(i,j) = LOC(1,1) + 前i-1行非零元素个数*size + 第i行中aij前非零元素个数*size = LOC(1,1) + (i*(i-1)/2+j-1)*size

上三角矩阵与下三角矩阵类似。

2. 带状矩阵

所有非零元素都集中在以主对角线为中心的3条对角线的区域，其他区域均为零.

LOC(i,j) = LOC(1,1) + (2+3(i-2) + j-i+1)*size