线性判别准则&&线性分类编程实践

最新推荐文章于 2021-11-05 20:36:23 发布

IT23131

最新推荐文章于 2021-11-05 20:36:23 发布

阅读量519

点赞数

CC 4.0 BY-SA版权

文章标签：分类机器学习人工智能

本文链接：https://blog.youkuaiyun.com/IT23131/article/details/121168345

本文详细介绍了线性判别分析（LDA），包括方差分析、拉格朗日法和推导过程，并通过代码实现了LDA分类。同时，深入探讨了支持向量机（SVM）的基本原理，结合月亮数据集和鸢尾花数据集，展示了线性SVM、多项式核和高斯核的使用。最后，总结了LDA与SVM在人工智能算法中的应用价值。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

一.LDA

线性判别分析用到方差分析和拉个朗日的相关知识，在介绍线性判别分析之前，先介绍方差分析和拉格朗日的相关知识，然后介绍线性判别分析（LDA的推导过程）、最后利用马氏距离计算样本与两类的距离，对数据进行分类

1.方差分析

2.拉个朗日法

3 线性判别分析（LDA）的推导过程

假设有两类数据红色和蓝色，我们想通过线性判别分析对这两类数据进行分类。图1可以看到没有很好的把数据分开，而图二可以很好的把数据分开，线性判别分析的目的是求一个投影向量，这个投影向量可以很高的区分两类数据（针对二分类问题）

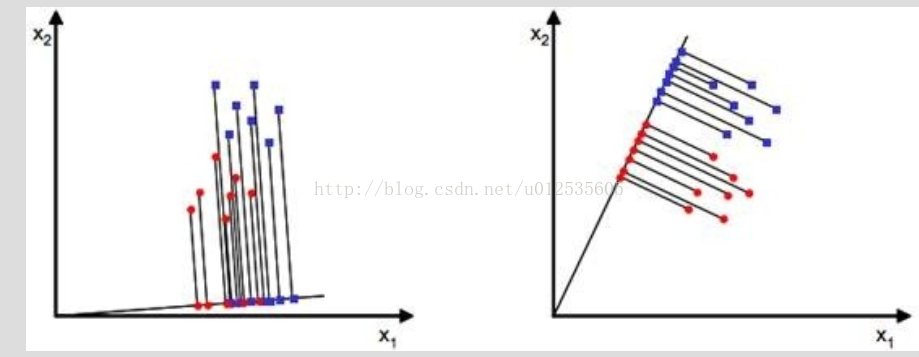
4.LAD代码实现

#####################################定义一个画图函数###########################
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
 
def plot_decision_regions(X, y, classifier, resolution=0.02):
 
    # setup marker generator and color map
    markers = ('s', 'x', 'o', '^', 'v')
    colors = ('red', 'blue', 'lightgreen', 'gray', 'cyan')
    cmap = ListedColormap(colors[:len(np.unique(y))])
 
    # plot the decision surface
    x1_min, x1_max = X[:, 0].min() - 1, X[:, 0].max() + 1
    x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max() + 1
    xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, resolution),
                           np.arange(x2_min, x2_max, resolution))
    Z = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T)
    Z = Z.reshape(xx1.shape)
    plt.contourf(xx1, xx2, Z, alpha=0.4, cmap=cmap)
    plt.xlim(xx1.min(), xx1.max())
    plt.ylim(xx2.min(), xx2.max())
 
    # plot class samples
    for idx, cl in enumerate(np.unique(y)):
        plt.scatter(x=X[y == cl, 0], 
                    y=X[y == cl, 1],
                    alpha=0.6, 
                    c=cmap(idx),
                    edgecolor='black',
                    marker=markers[idx], 
                    label=cl)
 
 
##############################数据的读入、划分、标准化###########################
import pandas as pd
#Python Data Analysis Library 或 pandas 是基于NumPy 的一种工具，该工具是为了解决数据分析任务而创建的。
#Pandas 纳入了大量库和一些标准的数据模型，提供了高效地操作大型数据集所需的工具。
df_wine = pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases