【Python】什么是递归函数？

最新推荐文章于 2025-10-14 22:00:36 发布

原创最新推荐文章于 2025-10-14 22:00:36 发布 · 4.6k 阅读

22 ·

CC 4.0 BY-SA版权

python 专栏收录该内容

23 篇文章

订阅专栏

本文介绍了递归函数的概念和特点，并通过实例展示了如何使用递归函数计算阶乘、斐波那契数列以及解决小明记单词的问题。递归函数以简洁的代码解决了这些问题，但需要注意递归的终止条件和效率。同时提到了尾递归优化，以及递归在分形和表达式中的应用。

3.2.斐波那契数列 0, 1, 1, 2, 3, 5, 8, 13, 21, ···

3.3.小明为了学好英语，需要每天记单词，第一天记1个，第二天记2个依次类推，请用代码完成，算出小明第10天开始的时候会了多少个单词？

4.拓展

1.递归函数的概念

递归就是一个函数在它的函数体内调用它自身。执行递归函数将反复调用其自身，每调用一次就进入新的一层。递归函数必须有结束条件。

2.递归函数的特点

递归函数的有点：代码简单，逻辑清晰

理论上所有的递归函数都可以写成循环迭代的方式

1. 每一级函数调用时都有自己的变量，但是函数代码并不会得到复制，如计算5的阶乘时每递推一次变量都不同；
2. 每次调用都会有一次返回，如计算5的阶乘时每递推一次都返回进行下一次；
3. 递归函数中，位于递归调用前的语句和各级被调用函数具有相同的执行顺序；
4. 递归函数中，位于递归调用后的语句的执行顺序和各个被调用函数的顺序相反；
5. 递归函数中必须有终止语句。

3.递归函数解决实际问题

3.1.计算n!=123...*n

def fact(n):
	if n < 2:
		return 1
	return n*fact(n-1)
print(fact(4))

>>24

3.2.斐波那契数列 0, 1, 1, 2, 3, 5, 8, 13, 21, ···

这个数列从第三项开始,每一项都等于前两项之和

def fibo(n):
	if n < 2:
		return n
	return fibo(n-1)+fibo(n-2)
print(fibo(5))

>>>5

我们把工作原理流程图简化成这种二叉树的模式，我们将通过树状结构来了解fibo(5)函数的执行流程。

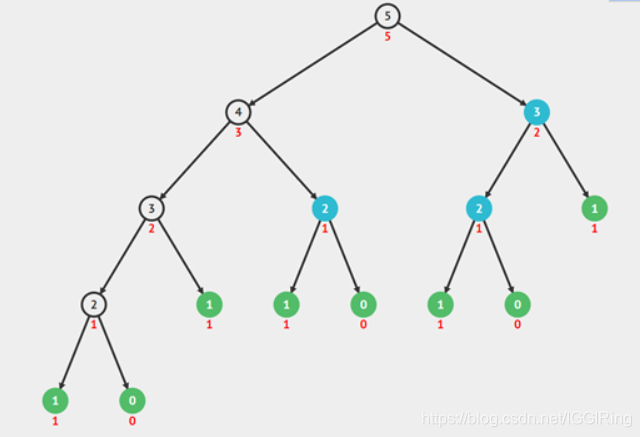
二叉树是先执行左边树枝，右分支是从最底层往上执行的

3.3.小明为了学好英语，需要每天记单词，第一天记1个，第二天记2个依次类推，请用代码完成，算出小明第10天开始的时候会了多少个单词？

def learn(n):
	if n < 2:
		return 1
	return n+learn(n-1)
print(learn(10))

>>>55

4.拓展

1.在计算机学里，尾调用是指一个函数里的最后一个动作是返回一个函数的调用结果的情形，即最后一步新调用的返回值直接被当前函数返回的情形。此时，该尾部调用位置被称为尾位置。若这个函数在尾位置调用本身（或是一个尾调用本身的其他函数等等），则称这种情况为尾递归，是递归的一种特殊情形。尾调用不一定是递归调用，但是尾递归特别有用，也比较容易实现。尾递归函数的特点是在回归过程中不用做任何操作，这个特性很重要，因为大多数现代的编译器会利用这种特点自动生成优化的代码。可参考链接如下：

python使用递归、尾递归、循环三种方式实现斐波那契数列https://blog.youkuaiyun.com/together_cz/article/details/76216239

2.使用python语言表达分形与递归，可参考链接如下：

http://wiki.swarma.net/index.php/%E4%BD%BF%E7%94%A8python%E8%AF%AD%E8%A8%80%E8%A1%A8%E8%BE%BE%E5%88%86%E5%BD%A2%E4%B8%8E%E9%80%92%E5%BD%92

3.参考其他文章：什么是递归函数https://blog.youkuaiyun.com/wf19930209/article/details/79341939#%E7%89%B9%E7%82%B9