一、简介
SVM,全名为支持向量机(Support Vector Machine),是一种应用广泛的有监督分类算法。它的基本模型是在特征空间上找到最佳的分割超平面使得训练集上正负样本间隔最大,通常用来解决二类问题,即标记只有两类。
二、原理
SVM的主要思想是找出一个最佳的能够分开两类数据的超平面,并根据该超平面对测试数据进行预测。根据要分类的数据集不同,有线性可分和线性不可分两种情况。
2.1 线性可分
当数据集线性可分时,我们可以用一个超平面将数据集中标记不同的两类数据在坐标轴上对应的点完全分开。在二维空间中用一条直线分割,在三维空间中用一个平面分割,以此类推。我们可以将这个超平面定义为:
wTx+b=0
\bold{w}^T\bold{x}+b=0
wTx+b=0
其中w\bold{w}w和x\bold{x}x均为向量,w\bold{w}w为法向量,表示超平面的方向;x\bold{x}x为数据实例。bbb为偏移量,表示超平面到原点的距离。将向量展开后,该公式可化为:
∑i=1nwTxi+b=0
\sum_{i=1}^n\bold{w}^T\bold{x}_i+b=0
i=1∑nwTxi+b=0
下面举例说明:
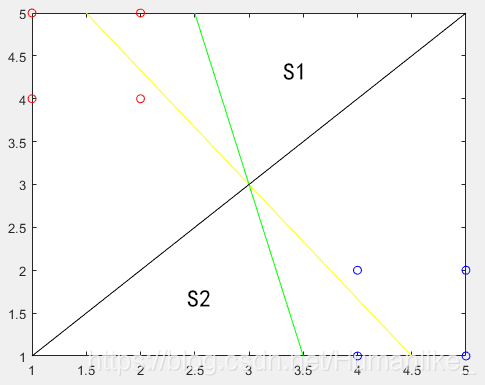
在上图中有红、蓝两类点,现在我们需要找到一个超平面将这两类点分开,对比黄、绿、黑三条线:首先排除黄线,因为它并没有将两类点完全分开;绿线和黑线中,看起来黑线更适合作为分类标准,因为若以绿线为标准,S1区域中的点应该为蓝点,S2区域中的点应为红点,但从逻辑上判断,可能相反的结果更合理,即以黑线为标准。在SVM中,我们引入间隔的概念来判断一个超平面是否适合作为分类标准。间隔即为该超平面上下两侧距离其最近的点与其的距离之和,间隔越大,分类时越准确。
在SVM算法中,我们选择的是最大间隔超平面(MMH,Max Margin Hyperplane)。若一超平面为MMH,则对于任意(xi,yi)(\bold{x}_i,y_i)(xi,yi),应有:
{wTxi+b≥1yi=1wTxi+b≤1yi=−1
\begin{cases}
\bold{w}^T\bold{x}_i+b≥1& y_i=1\\
\bold{w}^T\bold{x}_i+b≤1& y_i=-1
\end{cases}
{wTxi+b≥1wTxi+b≤1yi=1yi=−1
即:
yi(wTxi+b)≥1
y_i(\bold{w}^T\bold{x}_i+b)≥1
yi(wTxi+b)≥1
其中使等号成立的样本点与MMH的距离最近,被称为支持向量(support vector)。比如对于上图中的黑线,(2,4)(2,4)(2,4)和(4,2)(4,2)(4,2)即为支持向量。
由MMH方程可知,样本空间中任意一点到MMH的距离为:
r=∣wTx+b∣∣∣w∣∣
r=\frac{|\bold{w}^T\bold{x}+b|}{||\bold{w}||}
r=∣∣w∣∣∣wTx+b∣
故支持向量到MMH的距离为:
1∣∣w∣∣
\frac{1}{||\bold{w}||}
∣∣w∣∣1
故最大间隔为:
2∣∣w∣∣
\frac{2}{||\bold{w}||}
∣∣w∣∣2
其中∣∣w∣∣||\bold{w}||∣∣w∣∣为向量的范数(norm),计算公式为:
∣∣w∣∣=∑i=1nwi2
||\bold{w}||=\sqrt{\sum_{i=1}^{n}\bold{w}_i^2}
∣∣w∣∣=i=1∑nwi2
所以若要求间隔最大的超平面,只需求2∣∣w∣∣\frac{2}{||\bold{w}||}∣∣w∣∣2的最大值,即:
maxw,b 2∣∣w∣∣s.t. yi(wTxi+b)≥1, i=1,2,3,…,m
\max\limits_{\bold{w},b}\ \ \frac{2}{||\bold{w}||}\\
s.t.\ \ y_i(\bold{w}^T\bold{x}_i+b)≥1,\ \ i=1,2,3,\dots,m
w,bmax ∣∣w∣∣2s.t. yi(wTxi+b)≥1, i=1,2,3,…,m
也就是∣∣w∣∣||\bold{w}||∣∣w∣∣的最小值,即:
minw,b 12∣∣w∣∣2s.t. yi(wTxi+b)≥1, i=1,2,3,…,m
\min\limits_{\bold{w},b}\ \ \frac{1}{2}{||\bold{w}||}^2\\
s.t.\ \ y_i(\bold{w}^T\bold{x}_i+b)≥1,\ \ i=1,2,3,\dots,m
w,bmin 21∣∣w∣∣2s.t. yi(wTxi+b)≥1, i=1,2,3,…,m
这就是支持向量机的基本型。用拉格朗日乘子法可解得MMH的模型:
f(x)=wTx+b=∑i=1maiyixiTx+b
f(\bold{x})=\bold{w}^T\bold{x}+b=\sum_{i=1}^ma_iy_i\bold{x}_i^T\bold{x}+b
f(x)=wTx+b=i=1∑maiyixiTx+b
其中b{b}b的值为:
b=1∣S∣∑s∈S(1ys−∑i∈SaiyixiTxs)
b=\frac{1}{|S|}\sum_{s∈S}\left(\frac{1}{y_s}-\sum_{i∈S}a_iy_i\bold{x}_i^T\bold{x}_s\right)
b=∣S∣1s∈S∑(ys1−i∈S∑aiyixiTxs)
2.2 线性不可分
当数据集线性不可分时,在该维度内不存在可以区分两类数据的超平面,如下图:
此时,我们需要用一个映射函数将数据映射到一个线性可分的高维空间中,找到对应的MMH,再将数据映射回原维度空间。





 本文详细介绍了支持向量机(SVM)这一有监督分类算法,包括其原理、如何寻找最大间隔超平面以及在数据线性可分与线性不可分情况下的处理策略。
本文详细介绍了支持向量机(SVM)这一有监督分类算法,包括其原理、如何寻找最大间隔超平面以及在数据线性可分与线性不可分情况下的处理策略。

















 1165
1165

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










