opencv-12-高斯滤波-双边滤波(附C++代码实现)

开始之前

这几天由于自己的原因没有写, 一个是因为自己懒了, 一个是感觉这里遇到点问题不想往下写了, 我们先努力结束这个章节吧, 之前介绍了比较常用而且比较好理解的均值和中值滤波, 但是呢,在例程Smoothing Images, 还有给出的其他的滤波方式, 主要是高斯滤波和双边滤波,

我们这一次完结掉滤波与平滑的这个部分, 写的有点多了,反而不想再写了, 加油

目录

本文目标

本文主要是介绍

• 高斯滤波
• 双边滤波

和之前介绍的一样, 我们仍然还是 介绍一下原理, 给出一下具体的形式, 然后使用 opencv 进行一下实现的过程, 最后使用我们之前的图像进行测试 进行算法的分析与总结.

正文

高斯滤波(Gaussian Filter)

我们在之前介绍了中值滤波是统计排序的结果, 属于非线性的结果, 均值滤波是使用模板核进行的操作, 我们在的文章中也提到了均值滤波在计算的过程中必须要考虑权重的问题, 进而提出了加权的均值滤波的操作, 比如最常见的加权均值滤波的操作核.
$$M=\frac{1}{16}\left[\begin{array}{ccc}1& 2& 1\\ 2& 4& 2\\ 1& 2& 1\end{array}\right]$$

其实呢,这个核也就是高斯滤波器在 3*3窗口的离散取整的结果值, 最明显的特点就是模板的系数随着距离模板中心的距离而变换, 能够有效的抑制噪声,平滑图像, 相比均值滤波能够更好的平滑图像, 保留图像边缘.

高斯滤波原理

由于我们的图像是二维的, 但是高斯分布是一维的, 那我们先考虑一维的高斯分布, 就是我们常用的正太分布曲线,
$$G(x)=\frac{1}{\sqrt{2\pi \sigma }}{e}^{-\frac{x^2}{2{\sigma }^2}}$$

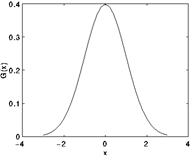
对于二维的高斯分布其实可以考虑成两个方向的运算相叠加的得到的结果
$$G(x,y)=\frac{1}{2\pi {\sigma }^2}{e}^{-\frac{x^2+y^2}{2{\sigma }^2}}=G(x)\ast G(y)$$

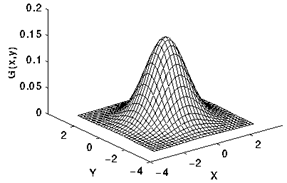
考虑到图像的计算实际上是离散的座标, 对于窗口大小为 $(2k+1)\times (2k+1)$ 模板, 我们可以表示成
$$Gi,j=\frac{1}{2\pi {\sigma }^2}{e}^{-\frac{(i-k-1{)}^2+(j-k-1{)}^2}{2{\sigma }^2}}$$

可以参考图像处理基础(4)：高斯滤波器详解
里面给出的方法, 使用

void generateGaussianTemplate(double window[][11], int ksize, double sigma)
{
   
   
    static const double pi = 3.1415926;
    int center = ksize / 2; // 模板的中心位置，也就是坐标的原点
    double x2, y2;
    for (int i = 0; i < ksize; i++)
    {
   
   
        x2 = pow(i - center, 2);
        for (int j = 0; j < ksize; j++)
        {
   
   
            y2 = pow(j - center, 2);
            double g = exp(-(x2 + y2) / (2 * sigma * sigma));
            g /= 2