【数据结构】计数排序

目录

一.核心思想：

二.思考与改进：

三.代码：

四.注意与缺陷：

---

一.核心思想：

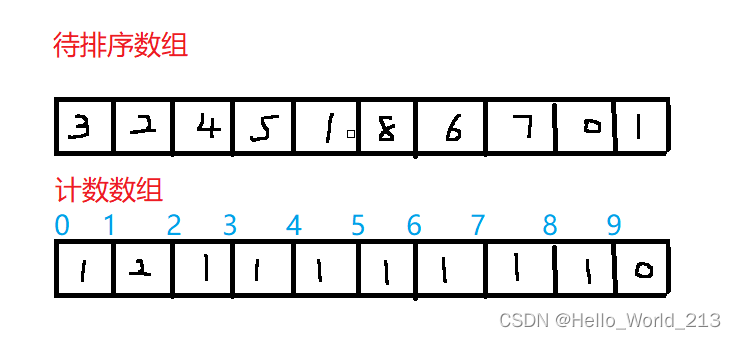
用一个数组来计数，数组所对应的下标与要排序的数组的值一一对应，然后根据计数的数组从下标为0开始一直到结束，根据计数依次放入下标值

 二.思考与改进：

1.上面的例子没有9这个数，开辟与原数组一样大小的计数数组是不是会有很多的空间浪费？

答：确实会有很多空间浪费，所以我们改进：先计算待排序数组的最大值Max与最小值Min，然后通过公式Max-Min+1计算出要开辟的最合适的计数数组的大小

2.数组的下标是没有负数的，如果一组数据中有负数怎么办？

假设待排序数组名为arr，计数数组名为count，在计数数组中计数时，用这种方式

count[arr[i]-Min]，让数组中的值减去最小值就一定不会出现负数了，通过计数数组依次放回原待排序数组时，只需要每个值再加上Min即可

三.代码：

void CountSort(int* arr, int n)
{
	//找最大最小求范围
	int min = arr[0];
	int max = arr[0];
	for (int i = 0; i < n; i++)
	{
		if (arr[i] > max)
			max = arr[i];
		if (arr[i] < min)
			min = arr[i];
	}
	int range = max - min + 1;
	//开辟空间并初始化为0
	int* tmp = (int*)calloc(range, sizeof(int));
	if (tmp == NULL)
	{
		printf("calloc failed\n");
		exit(0);
	}
	//memset(tmp, 0, sizeof(int) * range);
	//将对应数据改进后与tmp数组的下标一一对应且存入计数
	for (int i = 0; i < n; i++)
	{
		tmp[arr[i] - min]++;
	}
	//根基tmp中的计数，将tmp下标按顺序拷回arr
	int j = 0;
	for (int i = 0; i < range; i++)
	{
		while (tmp[i]--)
		{
			arr[j++] = i + min;
		}
	}
}

四.注意与缺陷：

开辟好计数数组后，一定要将数组所有元素初始化为0，因为需要依靠计数还原待排序数组。

计数排序适用于数据跨度小且集中的数据集，效率非常优，但是如果数据跨度大就会造成不必要的空间浪费