吴恩达深度学习笔记(29)-神经网络训练的方差和偏差分析

这一节我们学习在神经网络学习训练时出现的结果进行分析，偏差和方差的表现和优化，仔细看好咯~

偏差，方差（Bias /Variance）
几乎所有机器学习从业人员都期望深刻理解偏差和方差，这两个概念易学难精，即使你自己认为已经理解了偏差和方差的基本概念，却总有一些意想不到的新东西出现。

关于深度学习的误差问题，另一个趋势是对偏差和方差的权衡研究甚浅，你可能听说过这两个概念，但深度学习的误差很少权衡二者，我们总是分别考虑偏差和方差，却很少谈及偏差和方差的权衡问题，下面我们来一探究竟。

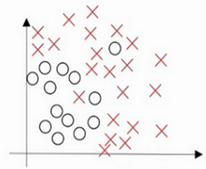
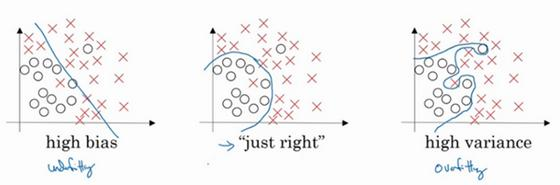
假设这就是数据集，如果给这个数据集拟合一条直线，可能得到一个逻辑回归拟合，但它并不能很好地拟合该数据，这是高偏差（high bias）的情况，我们称为“欠拟合”（underfitting）。

相反的如果我们拟合一个非常复杂的分类器，比如深度神经网络或含有隐藏单元的神经网络，可能就非常适用于这个数据集，但是这看起来也不是一种很好的拟合方式分类器方差较高（high variance），数据过度拟合（overfitting）。

在两者之间，可能还有一些像图中这样的，复杂程度适中，数据拟合适度的分类器，这个数据拟合看起来更加合理，我们称之为“适度拟合”（just right）是介于过度拟合和欠拟合中间的一类。

在这样一个只有x_1和x_2两个特征的二维数据集中，我们可以绘制数据，将偏差和方差可视化。在多维空间数据中，绘制数据和可视化分割边界无法实现，但我们可以通过几个指标，来研究偏差和方差。