线性回归问题：Tensorflow2实战

---

前言

最近准备入门图像识别领域，在了解图像识别的基本原理之后但是苦于一直不知道该如何开始自己的第一个项目， 在看了几种不同的网课之后，终于发现了《深度学习应用开发-TensorFlow实践》。这是大学mooc的一门课，讲解浅显易懂，并且很容易上手。
程序源码：https://github.com/hu669293657/Tensorflow/tree/main

---

环境

Win10
Python3.9
Tensorflow2.6.0
PyCharm Community Edition 2021.2

---

一、基本原理和概念

1.线性回归

线性回归是来自于统计学的一个方法。函数的定义说的是 独立参数 x 和 非独立参数 y之间的对应关系。例如本文使用的例子：y=2x+1。

2.回归分析

在统计学中，回归分析（regression analysis)指的是确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法。

3.机器学习系统

通过学习如何组合输入信息来对未见过的数据做出有用的预测。

4.监督式机器学习

是一个机器学习中的方法，可以由训练资料中学到或建立一个模式（函数 / learning model），并依此模式推测新的实例。本文就是利用监督式机器学习来解决线性回归预测的问题。

5.标签和特征

标签是我们要预测的真实事物：y线性回归中的y变量。
特征是指用于描述数据的输入变量：xi，线性回归中的{x1，x2，…，xn）变量

6.超参数

在机器学习中，超参数是在开始学习过程之前设置值的参数，而不是通过训练得到的参数数据。

7.梯度下降法

这个方法在网上有很多专业的解释，但是对于初学者可能要花比较长的时间理解，在这里我说一下我的理解，可能不是很准确但是应该会好理解一点。对于本题中的线性方程y=2x+1，其中x和y已经给定，当我们让机器来预测这个方程时，即预测y=wx+b中的w和b。如图：

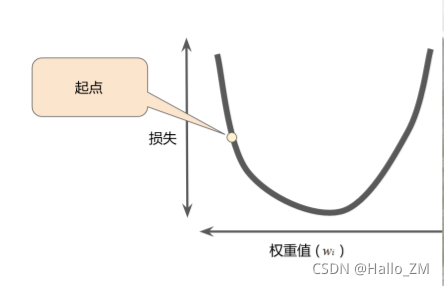
y轴是损失，即我们预测的w与真实的w的误差；x轴为权重，即我们现在的w。我们令w为一个初始值，即起点，通过不断得调整那个小圆珠在黑线上的位置，直到那个小圆珠到达了最底下的位置，即那一点导数非常接近于0。我们就认为我们预测的w和真实的w差距最小。所以我们就要一点点来调整小圆珠，在这过程中速度既不能太快也不能太慢，太快的话小圆珠就会像个摆钟一样在最低点反复横跳，太慢的话时间也就太长了也不太好。

二、进入实战

1.准备数据

第一步就是准备数据，正所谓巧妇难为无米之炊。通过设置w=2.0，b=1.0，并加入一个噪声，噪声最大振幅为0.4，否则就是y=2x+1的那条直线了，代码如下（示例）：

导入相关库

import matplotlib.pyplot as plt
import numpy as np
import tensorflow as tf

生成数据集，*x_data.shape为100

x_data = np.linspace(-1,1,100)
np.random.seed(5)  #设置随机数种子，来保证我们的随机数都是一样的
y_data = 2*