编译原理--有限自动机

先了解有限状态机（FSM）

编译器就是用有限状态机做词法分析

有限状态机就是一个集合很多状态的机器，根据不同的输入产生不同的状态转变，通过这些状态的转变来体现出每次用户操作的特殊性。状态的产生和改变都是由某种条件成立而出现的

有限自动机（有穷自动机，时序机）：

有限自动机M由五元组（X,Y,S,δ,λ)

• X,Y是S的非空有限集
• X：输入集
• Y：输出集
• S：状态集合
• δ：笛卡尔积SxX到S的映射，也叫M的下一状态函数
• λ：SxY到Y的单值映射，也叫M的输出函数

有限自动机 = 内部状态集+控制规则

有限状态机识别字符串：

比如：源代码一个语句为输入字符串，判断其是否能使用有限自动机从初始状态到终状态结束，能，则可以被识别

状态转换图是一个有向图，每个节点表示一个状态，每一个状态转换都对应一个弧

分类：

确定的有限自动机和不确定的有限自动机：

区别：

确定的有限自动机（DFA）：

• 开始状态唯一
• 一个输入对应一个状态转换

不确定的有限自动机（NFA）：

• 开始状态为一个状态集合
• 一个输入对应多个状态转换
• 有向弧的标记上可以为空

NFA到DFA的转换过程：

状态转换表

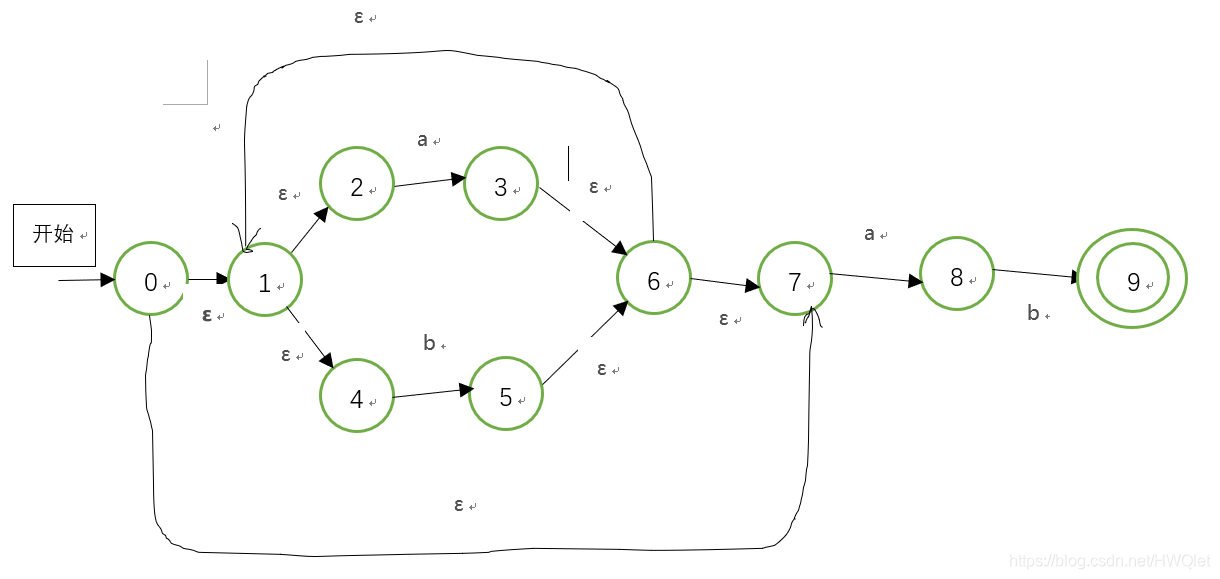
	a	b	ε
0	#	#	1,7
1	#	#	2,4
2	3	#	#
3	#	#	6
4	#	5	6
5	#	#	6
6	#	#	1,7
7	8	#	#
8	#	9	#
9	#	#	#

 然后我们可以得出ε-closure(s)，即从s出发，经由条件ε可以到达的状态集要包括当前状态：

ε-closure(0)：{0，1，2，4，7}

ε-closure(1)：{1，2，4}

ε-closure(2)：{2}

ε-closure(3)：{1，2，3，4，6，7}

ε-closure(4)：{4}

ε-closure(5)：{1，2，4，5，6，7}

ε-closure(6)：{1，2，4，6，7}

ε-closure(7)：{7}

ε-closure(8)：{8}

ε-closure(9)：{9}

然后我们需要进行简化，把全新的状态A=ε-closure(0)={0，1，2，4，7}

接着求出状态A经过除了ε条件的其他条件转换得到的状态集，这叫后继状态，后继状态不包括自身

A=ε-closure(0)

ε-closure(move(A,a))=ε-closure({3，8})={1，2，3，4，6，7，8}--->全新的状态集设为=B

ε-closure(move(A,b))=ε-closure({5})={1，2，4，5，6，7}---->全新的状态集设为=C

现在就多了两个新状态B，C

ε-closure(move(B,a))=ε-closure({3，8})={1，2，3，4，6，7，8}---->已有的状态B

ε-closure(move(B,b))=ε-closure({5，9})={1，2，4，5，6，7，9}---->全新的状态集设为=D

ε-closure(move(C,a))=ε-closure({3，8})={1，2，3，4，6，7，8}---->已有的状态B

ε-closure(move(C,b))=ε-closure({5})={1，2，4，5，6，7}---->已有的状态C

ε-closure(move(D,a))=ε-closure({3，8})={1，2，3，4，6，7，8}---->已有的状态B

ε-closure(move(D,b))=ε-closure({5})={1，2，4，5，6，7}---->已有的状态C

至此，没有产生新状态，且每个状态的条件都组合完成

然后画出DFA状态转换表（每个状态只有一个后继状态）：

	a	b
A	B	C
B	B	D
C	B	C
D	B	C

 画出状态转换图：

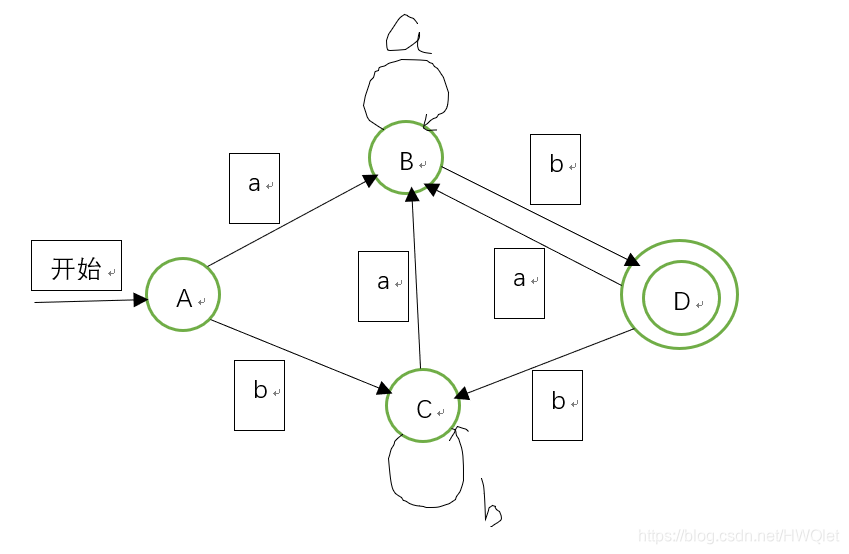
然后进行DFA的最小化：

• 消除多余状态
  • 多余状态情况：
    • 从这个状态出发没有通路到达终态
    • 从开始状态出发，任何输入串都不能到达那个状态（没有一条通路到达那个状态）
  • 处理：
    • 删除即可
• 合并等价状态
  • 等价状态条件：对于两个可以合并的状态s和t满足以下条件
    • 一致性条件：状态s和状态t必须同时为终态或者非终态（终态可以不止一个，开始只有一个）
    • 蔓延性条件：对于所有输入符号，状态s和t必须转换到等价的状态里

上面的图可以看出没有多余状态

再看有没有等价状态可以合并：AB，AC，BC都可以合并，但要保证合并之后的状态最少就行

所以合并如下;

	a	b
I(A|B)	B B	C D
II(C)	B	C
III(D)	B	C

画出合并后的状态转换图：

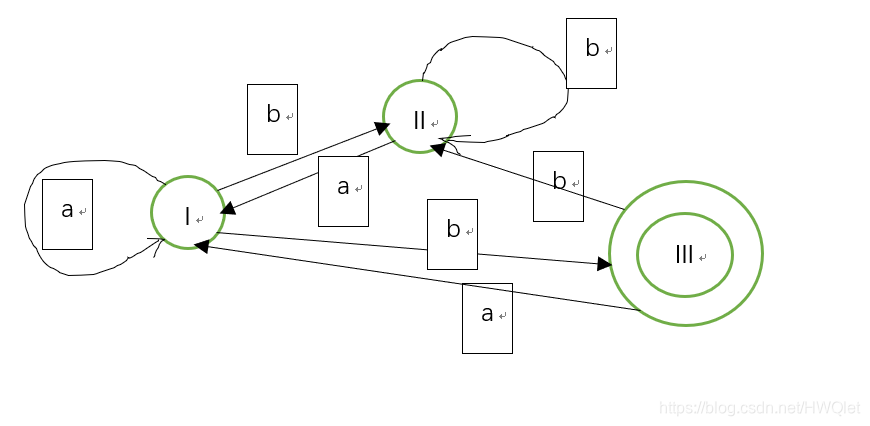
ok了