python基本数据结构：栈、队列、双端队列、链表和二叉树

一、栈

1.1、什么是栈

        栈（有时称为“后进先出栈”）是一个项的有序集合，其中添加移除新项总发生在同一端。这一端通常称为“顶部”。与顶部对应的端称为“底部”。栈的底部很重要，因为在栈中靠近底部的项是存储时间最长的。最近添加的项是最先会被移除的。这种排序原则有时被称为 LIFO，后进先出。它基于在集合内的时间长度做排序。较新的项靠近顶部，较旧的项靠近底部。
       栈的例子很常见。几乎所有的自助餐厅都有一堆托盘或盘子，你从顶部拿一个，就会有一个新的托盘给下一个客人。想象桌上有一堆书(Figure 1), 只有顶部的那本书封面可见，要看到其他书的封面，只有先移除他们上面的书。Figure 2 展示了另一个栈，包含了很多 Python 对象。

1.2、Python实现栈

        代码实现1：

       在python中，抽象数据类型的选择实现是创建一个新类，栈操作实现为类的方法，此外，为了实现作为元素集合的栈，使用由Python提供的原语集合的能力是有意义的，我们将使用列表作为底层实现。

 

class stack():
	def __init__(self):
		self.items = []
	
	def isEmpty(self):
		return self.items == []
	
	def push(self,item):
		self.items.append(item)
	
	def pop(self):
		return self.items.pop()
	
	def peek(self):
		return self.items[len(self.items) - 1]
	
	def size(self):
		return len(self.items)
	

       代码实现2：

       我们通过实例化Stack类执行栈的操作，Stack 类的定义是从 pythonds 模块导入的。

from pythonds.basic.stack import Stack

s = Stack()

s.push(4)            #栈从顶部添加元素，相当于age1中列表 append
s.push('dog')
print(s.peek())      #栈展示顶部的第一个元素，相当于age1中的peek
s.push(True)
print(s.size())        #显示栈中有几个元素
print(s.isEmpty())   #显示栈中是否有元素
s.push(8.4)
print(s.pop())       #栈删除最顶部的元素，并返回元素

1.3 栈解决实际问题

      age1:

              栈可以用来判断一个算术表达式中的括号是否匹配。

def parChecker(str_):
	
	i,state = 0,True
	s = Stack()
	
	while i < len(str_) and state:

		if str_[i] == "(":
			s.push(str_[i])
		else:
			if s.isEmpty():   #排除右边括号多于左边括号的情况
				state = False
			else:
				s.pop()
		i += 1
	if s.isEmpty() and state:#s.isEmpty()自动排除左边括号多于右边括号的情况~
		return True
		
	else:
		return False
		

print(parChecker('((()))'))
print(parChecker('(()'))

 

      age2:

              这个是age1的升级版，栈可以用来判断一个算术表达式中的括号（混合符号：{ { ( [ ] [ ] ) } ( ) }）是否匹配。

              这个代码基本和age1一样，只是增加了一个字典用来匹配从顶部去掉的左边符号和右边符号是否相等~

from pythonds.basic.stack import Stack
def parChecker(str_):
	str_ = [i for i in str_ if i!= ' '] #去除掉括号字符中的空格
	i, state = 0, True
	s = Stack()
	c = {'{':'}','(':')','[':']'}       #构建一个字典用于匹配左右字符
	
	while i < len(str_) and state:
		
		if str_[i] in  "({[":
			s.push(str_[i])
		else:
			if s.isEmpty():  # 排除右边括号多于左边括号的情况
				state = False
			else:
				a = s.pop()
				
				if c[a] != str_[i]:
					state = False
					break
		i += 1
	if s.isEmpty() and state:  # s.isEmpty()自动排除左边括号多于右边括号的情况~
		return True
	
	else:
		return False


print(parChecker('(([()]))'))
print(parChecker('[{() }]'))

      age3:

              将二进制转化成n进制。

from pythonds.basic.stack import Stack
def baseConverter(number,base):
	s = Stack()
	c = {10:'十',11:'十一',12:'十二',13:'十三',14:'十四',15:'十五'}
	while number > 0:
		a = number % base
		s.push(a)
		number = number // base
		
	b = ''
	while not s.isEmpty():
		b = b +  c[s.pop()] if s.pop() > 9 else s.pop()

	return b

二、队列

2.1、什么是队列

        队列是项的有序结合，其中添加新项的一端称为队尾，移除项的一端称为队首。当一个元素从队尾进入队列时，一直向队首移动，直到它成为下一个需要移除的元素为止。

       最近添加的元素必须在队尾等待。集合中存活时间最长的元素在队首，这种排序成为 FIFO，先进先出，也被成为先到先得。

2.2、Python实现队列

        我们为了实现队列抽象数据类型创建一个新类。和前面一样，我们将使用列表集合来作为构建队列的内部表示。

        python实现1：

 

class queen:
	
	def __init__(self):
		self.items = []
		
	def isEmpty(self,item):
		return self.items == []
	
	def enqueue(self,item):
		self.items.insert(0, item)
		
	def dequeue(self):
		return self.items.pop()
		
	def size(self):
		return len(self.items)

         Python实现2:

from pythonds.basic.queue import Queue

s = Queue()

s.enqueue(4)           #队列从队尾添加元素，相当于实现1中列表 insert(0,item)
s.enqueue('dog')
s.enqueue(True)
print(s.size())       #显示队列中有几个元素
print(s.isEmpty())   #显示队列中是否有元素
s.enqueue(8.4)
print(s.dequeue())   #队列删除队首的元素，并返回元素

2.3 队列解决实际问题 

        著名的约瑟夫问题，一个一世纪著名历史学家弗拉维奥·约瑟夫斯的传奇故事。故事讲的是，他和他的 39 个战友被罗马军队包围在洞中。他们决定宁愿死，也不成为罗马人的奴隶。他们围成一个圈，其中一人被指定为第一个人，顺时针报数到第七人，就将他杀死。约瑟夫斯是一个成功的数学家，他立即想出了应该坐到哪才能成为最后一人。

       我们模拟这个过程，我们的程序将输入名称列表和一个称为 num 常量用于报数。它将返回以 num 为单位重复报数后剩余的最后一个人的姓名。

from pythonds.basic.queue import Queue
def hotPotato(namelist, num):
	simqueue = Queue()
	for name in namelist:
		simqueue.enqueue(name)
	while simqueue.size() > 1:
		for i in range(num):
			a = simqueue.dequeue()
			print(a)
			simqueue.enqueue(a)
		b = simqueue.dequeue()
	return simqueue.dequeue()
print(hotPotato(["Bill","David","Susan","Jane","Kent","Brad"],7))

三、双端队列

3.1、什么是双端队列

        deque（也称为双端队列）是与队列类似的项的有序集合。它有两个端部，首部和尾部，并且项在集合中保持不变。deque 不同的地方是添加和删除项是非限制性的。可以在前面或后面添加新项。同样，可以从任一端移除现有项。在某种意义上，这种混合线性结构提供了单个数据结构中的栈和队列的所有能力。

3.2、Python实现Deque

        我们将为抽象数据类型 deque 的实现创建一个新类。同样，Python 列表将提供一组非常好的方法来构建 deque 的细节。我们的实现（Listing 1）将假定 deque 的尾部在列表中的位置为 0。

        python实现1：

class Deque: 
	def __init__(self): 
		self.items = []
		
	def isEmpty(self): 
		return self.items == []
	
	def addFront(self, item):  #从首部增加元素
		self.items.append(item)
		
	def addRear(self, item):  #从尾部增加元素
		self.items.insert(0, item)
	
	def removeFront(self):    #从首部删除元素
		return self.items.pop()
		
	def removeRear(self):     #从尾部增加元素
		return self.items.pop(0)
	
	def size(self): 
		return len(self.items)

        python实现2：

from pythonds.basic.deque import Deque

que = Deque()
que.addRear('周剑辉')         #从尾部添加元素
que.addFront('梁菲菲')        #从头部增加元素
que.addRear('苏焕姐')
print(que.size())             #3
print(que.isEmpty())          #False
print(que.removeFront())      #从头部去除元素并返回这个元素('梁菲菲')
print(que.removeRear())       #从头部去除元素并返回这个元素('苏焕姐')

3.3 Deque解决实际问题 

       回文检查：

       思路：使用deque来存储字符串的字符，然后分别从首部和尾部去下一个字符进行对比，判断是否相等，直到deque中无字符或者只剩下一个字符。

def func(aString):
	aa = Deque()
	for i in aString:
		aa.addRear(i)
		
	while aa.size() > 1:
		first = aa.removeRear()
		last = aa.removeFront()
		if first == last:
			continue
		else:
			return False
	
	return True
	
a = func('周剑辉2辉剑周')
print(a)

四、链表

4.1、什么是链表

       链表是一种物理存储单元上非连续、非顺序的存储结构，数据元素的逻辑顺序是通过链表中的指针链接次序实现的。链表由一系列节点（链表中每一个元素称为结点）组成，节点可以在运行时动态生成。每个节点包括两个部分：一个是存储数据元素的数据域，另一个是存储下一个结点地址的指针域。 相比于线性表顺序结构，操作复杂。由于不必须按顺序存储，链表在插入的时候可以达到O(1)的复杂度，比另一种线性表顺序表快得多，但是查找一个节点或者访问特定编号的节点则需要O(n)的时间。

 

       链表实现的基本构造块是节点。每个节点对象必须至少保存两个信息。首先，节点必须包含列表项本身。我们将这个称为节点的数据字段。此外，每个节点必须保存对下一个节点的引用。

4.2、python实现对节点和链表的构造

        Python实现对节点的构造：

class Node():
	def __init__(self,initdata):
		self.data = initdata     #节点的数据字段
		self.next = None         #节点保存对下一个节点的引用（初始值为None)
		
	def getData(self):           #获取节点的数据字段
		return self.data
	
	def getNext(self):           #获取节点中 保存的 对下一个节点的引用值
		return self.next
	
	def setData(self,newdata):   #重新设立节点的数据字段
		self.data = newdata
	
	def setNext(self,newnext):   #重新设立节点对下一个节点的引用值
		self.next = newnext

 

>>> temp = Node(93)

>>> temp.getData()

93

       Python实现对链表的构造：

       链表类必须保持对第一个节点的引用。Listing 2 显示了构造函数。注意，每个链表对象将维护对链表头部的单个引用。

class UnorderedList():
	def __init__(self):
		self.head =  None #作为对链表第一个节点的引用
	

        下面所示的 isEmpty 方法只是检查链表头是否是 None 的引用。 布尔表达式 self.head== None 的结果只有在链表中没有节点时才为真（否则self.head保存的是下一个Node的对象）。由于新链表为空，因此构造函数和空检查必须彼此一致。这显示了使用引用 None 来表示链接结构的 end 的优点。

	def isEmpty(self):
		return self.head == None

        如何将节点加入到链表中，我们用add方法来实现，由于链表是无序的，所以新节点相对于链表中的其他的特定节点的特定位置并不重要，新节点放在最简单的位置的最方便。

        链表结构只为我们提供了一个入口点，添加新节点的最简单的地方就在链表的头部。

	def add(self,item):
		temp = Node(item)      #形成一个新的节点（新节点的引用为None）
		temp.setNext(self.head)#更改新节点的下一个引用以引用旧链表的第一个节点（第三步）
		self.head = temp       #将新节点的对象作为新链表的head        （第四步）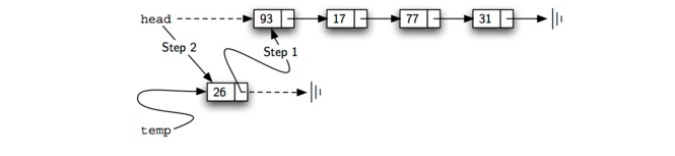

 

        实现size方法：我们需要遍历链表并对节点数计数，刚开始我们把链表的头部赋值给变量current，如果current不为None(即没有遍历到最后一个节点，我们就不断的移动位置，将前一个节点的引用赋值给current。

	def size(self):
		current = self.head
		total = 0
		while current != None:
			total += 1
			current = current.getNext()  #参考add方法中的代码，后一个节点总是保存前一个节点对象的引用（后一个节点（getnext)取引用取的就是前一个节点的对象）
			
		return  total

         实现search方法：和在 size 方法中一样，遍历从列表的头部开始初始化（行2）。我们还使用一个布尔变量叫 found ，标记我们是否找到了正在寻找的项。因为我们还没有在遍历开始时找到该项， found 设置为 False（第8行）。第4行中的迭代考虑了上述两个条件。只要有更多的节点访问，而且我们没有找到正在寻找的项，我们就继续检查下一个节点。第 5 行检查数据项是否存在于当前节点中。如果存在， found 设置为 True。

	def search(self,bool):
		current = self.head()
		found = False
		while current!= None and not found:
			if current.getData() != bool:
				current = current.getNext()
			else:
				found = True
		
		return found

          实现remove方法：在我们遍历链表时使用两个外部引用。 current 将像之前一样工作，标记遍历的当前位置。新的引用，我们叫 previous ，将总是传递 current 后面的一个节点。这样，当 current 停止在要被去除的节点时， previous 将引用链表中用于修改的位置（current之后的节点的对象）。

          注意， current 在链表头处开始，和在其他遍历示例中一样。然而， previous 假定总是在 current 之后一个节点。因此，由于在 previous 之前没有节点，所以之前的值将为 None（见 下图）。 found 的布尔变量将再次用于控制迭代。

          remove方法默认目标值是一定是存在链表中的！！！

	def remove(self,bool):
		current = self.head
		previous = None
		found = False
		while not found:
			if current.getData != bool:
				previous = current
				current = current.getNext()
			else:
				found = True
				
		if previous == None:           #避免那种第一个节点就是目标值得情况
			self.head = current.getNext()
		else:
			previous.setNext(current.getNext())

 

五、二叉树

5.1、树的属性

        第一个属性：树是分层的

        第二个属性：一个节点的多有子节点独立于另一个节点的子节点

        第三个属性：每个叶节点是唯一的，我们可以指定从树的根到唯一地识别树中每个子节点的路径。

5.2、词汇和定义

        节点

        节点是树的基本部分，它可以有一个名称，我们称之为“键”，节点也可以附加信息（我们称之为“有效载荷”），这个附加信息在利用树中通常是关键的。

        边

        这是树的另一个基本部分，边连接两个节点以显示它们之间存在关系，每个节点都可以有多个输出边。

        根

        树的根是树中唯一没有传入边的节点。

        路径

        路径是由边连接节点的有序列表。

        子节点

        具有来自相同传入边的节点c的集合称为该节点的子节点。

        父节点

        具有和它相同传入边的所连接的节点称为父节点。

        兄弟

        树中作为同一父节点的子节点的节点被称为兄弟节点。

        子树

        子树和由父节点和其所有后代组成的一组节点和边。

        叶节点

        叶节点就是没有子节点的节点

        层数

        节点n的层数为从根节点到该节点所经过的分支数目。例如：根节点的层数为零。

        高度

        树的高度等于树中任何节点中的最大层数。

        现在已经定义了树的基本词汇，我们可以继续对树的正式定义。我们提供对树的两个定义：

        第一个定义涉及节点和边

        第二个节点是一个递归定义

        定义一：树由一组节点和一组连接节点的边组成。树具有以下属性

        o 树的一个节点被指定为根节点

        o 除了根节点之外，每个节点n通过一个其他节点p的边连接，其中p是n的父节点。

        o 从根路径遍历到每个节点路径唯一

        o 如果从树中的每个节点最多有两个子节点，我们说该树是一个二叉树。

        定义二：树是空的，或者由一个根节点和零个或多个子树组成，每个子树也是一棵树。每个子树的根节点通过边连接到父树的根节点。

5.3、列表表示

        我们用python的列表数据结构开始，编写上面定义的函数。在列表树的列表中，我们将根节点的值储存为列表的第一个元素。元素的第二个元素本身将是一个表示左子树的列表，列表的第三个元素将是表示右子树的另一个列表。我们举一个例子。

myTree = ['a',   #root
		 ['b'    #left subtree
		   ['d',[],[]],
		   ['e',[],[]]],
		 ['c',#right subtree
		   ['f',[],[]],
		   []]
		  ]

        我们可以使用标准列表来访问列表的子树。树的根是myTree[0],根的左子树是myTree[1],根的右子树myTree[2],该列表方法一个非常好的属性是表示子树的列表的结构遵循树定义的结构；结构本身是递归的！具有根值和两个空列表的子树是叶节点(d和f)。列表方法的另一个很好的特性是它可以推广到一个有很多子树的树。在树超过二叉树的情况下，另一个子树只是另一个列表。

       

myTree = ['a', ['b', ['d',[],[]], ['e',[],[]] ], ['c', ['f',[],[]], []] ]
print(myTree)
print('left subtree = ', myTree[1])
print('root = ', myTree[0])
print('right subtree = ', myTree[2])

        让我们提供一些使我们能够使用列表作为树的函数来形式化树数据结构的这个定义，我们写的函数只是帮助我们操纵一个标准列表，就像我们正在使用一棵树。

def BinartTree(r): #构造一个具有根节点和两个子列表为空的列表
	return [r,[],[]]


def insertLetf(root,newBranch): #要将左子树添加到树的根，我们需要在根列表的第二个位置插入一个新的列表，如果列表已经在第二个位置有东西，我们需要跟踪她，并沿着树向下把它作为我们添加的列表的左子节点。
	t = root.pop(1)             #取出原列表中第二个位置的数
	if len(t) > 1:              #判断列表中的第二个位置是否有东西（此处有疑问不应该是长度判断是否大于零吗）
		root.insert(1,[newBranch,t,[]])
	else:
		root.insert(1,[newBranch,[],[]])

def insertRight(root,newBranch):#同上 插入右子节点
	t = root.pop(2)
	if len(t) > 1:
		root.insert(2,[newBranch,[],t])
	else:
		root.insert(2,[newBranch,[],[]])
	return root

def getRootVal(root):        #获取根节点
	return root[0]
def setRootVal(root,newVal): #设立根节点的值
	root[0] = newVal
def getLeftChild(root):      #获取左子树的值
	return root[1]
def getRightChild(root):     #获取右子树的值
	return root[2]

         我们的第二种表示树的方法使用节点和引用。在这种情况下，我们将定义一个具有根值属性的类，以及左和右子树，由于这个表示更接近于面向对象的编程范例，我们将继续使用这个表示法用于本章的剩余部分。

         使用节点和引用，我们认为树结构类似于下面所示：

                 

          我们将从节点和引用方法的一个简单的类定义开始，要记住这个比较重要的事情是leftChild 和rightChild 的属性将成为对BinaryTree类的其他实例的引用。

class BinaryTree:
	def __init__(self,rootObj):
		self.key = rootObj
		self.leftChild = None
		self.rightChild = None
		
		
	def insertLeft(self,newNode):
		if self.leftChild == None: #如果根的左边属性（左子树）为空，将根的左边属性来引用新对象
			self.leftChild = BinaryTree(newNode)
		else:                      #如果根的左边属性（左子树）不为空，先用新对象的左边属性（左子树）引用根的左边属性（左子树），然后根的左边属性（左子树）应用新对象
			t = BinaryTree(newNode)
			t.leftChild = self.leftChild
			self.leftChild = t
	
	def insertRight(self,newNode):
		if self.rightChild == None: #如果根的左边属性（左子树）为空，将根的左边属性来引用新对象
			self.rightChild = BinaryTree(newNode)
		else:                      #如果根的左边属性（左子树）不为空，先用新对象的左边属性（左子树）引用根的左边属性（左子树），然后根的左边属性（左子树）应用新对象
			t = BinaryTree(newNode)
			t.rightChild = self.rightChild
			self.rightChild = t
			
	def getRightChild(self):
		return self.rightChild
	
	def getLeftChild(self):
		return self.leftChild
	
	def setRootVal(self,obj):
		self.key = obj
		
	def getRootVal(self):
		return self.key
	
r = BinaryTree('a')    #使用节点a作为根的简单树
print(r.getRootVal())  #观察根节点
print(r.getLeftChild())#观察根的左节点
r.insertLeft('b')     #插入一个左节点b
print(r.getLeftChild().getRootVal()) #观察已经插入的左节点b(在根的左节点的位置）
r.insertRight('c')    #插入一个右节点c
print(r.getRightChild())#观察右节点对象
print(r.getRightChild().getRootVal()) ##观察已经插入的右节点c(在根的右节点的位置）
r.getRightChild().setRootVal('hello')
print(r.getRightChild().getRootVal())

           在本书的其余部分，我们将更详细的检查分析树，特别的，我们会看

1、如何从完全括号的数学表达式构建分析树。

2、如何评估存储在分析树中的表达式。

3、如何从分析树中恢复原始数学表达式。

           构建分析树的第一步是将表达式字符串拆分成符号列表。有四种不同的符号要考虑：左括号，右括号，运算符和操作数

 

 

 部分内容摘自：python-data-structure-cn