环形链表详解

一.如何判断链表是否成环

成环链表与不成环链表相比，有一个很明显的差异
成环链表中是不存在尾节点的

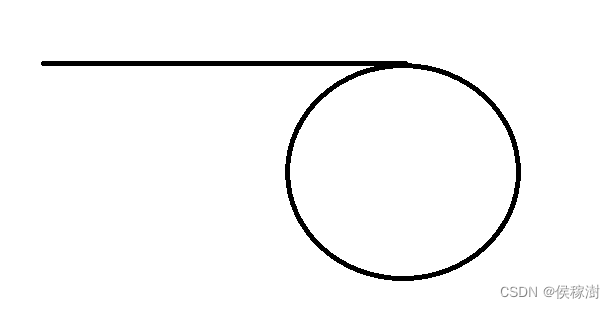
所有节点中的指针都是指向下一节点的
根据这个差异，便可以很好的分辨链表分辨出来
该如何利用这个差异呢？
诺在一个成环链表中寻其尾节点，定为死循环
但设计程序时，也不能将程序设计成死循环。
如果利用快慢指针，便可以很好的解决这个问题

假设 fast 指针一步前进2个节点
slow 指针一步前进1个节点

fast定先进入环，此后便在环内不断变量，就像打转一样。
slow指针会在之后的某一个时刻进入环中

fast 相对于 slow 的相对速度为1
定会在某一时刻二者相遇

代码如下所示

bool hasCycle(struct ListNode *head) {
    struct ListNode * slow = head;
    struct ListNode * fast = head;
    while(fast &&fast->next)
    {
        fast = fast->next->next;
        slow = slow->next;
        if(fast == slow)
        return true;
    }
    return false;
}

给定一个链表，判断链表中是否有环。
leetCode 141
大体过程如下图所示

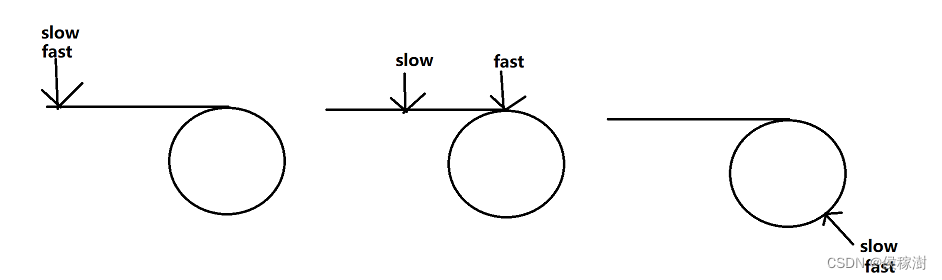
寻找环形数组入环的第一个节点

在探究这个问题之前，先来看一个数学问题
此问题建立在上一个问题的基础上
将指针前进一步抽象为单位长度

• 假设从起点到入环节点的距离为 L
• 环的周长为 C
• 两指针相遇时相对于头节点的距离为 X
• 
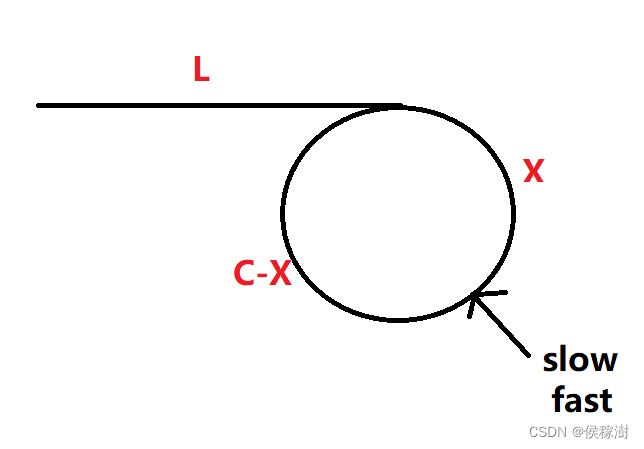
  先讨论一下俩指针的运动过程
  fast 先进入环后，在环内不断打转，知道slow进入环链表
  此时
  
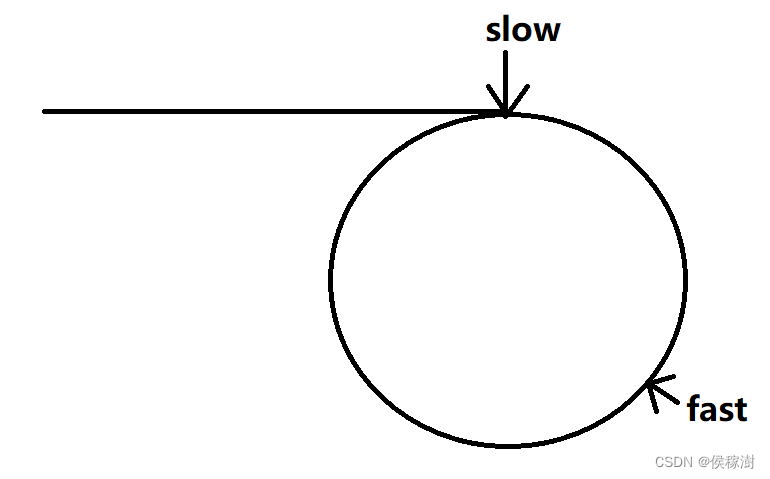
  二者间的相对距离最大时，应为 c-1
  fast 的速度为 2 slow 的速度为 1
  假设在两者相遇前，slow指针已在环链表中行驶一周
  那么速度为2 的fast指针，将在环内形式两周
  此必不可能
  那么，slow指针行驶的距离为 L+ X
  fast指针行驶的距离为 L+ X + nc
  因两指针同时出发 fast指针行驶的距离应该为slow指针的两倍
  即 L+X+nc = 2(L+X)
  推导一下 L = C-X +(N-1)C
  
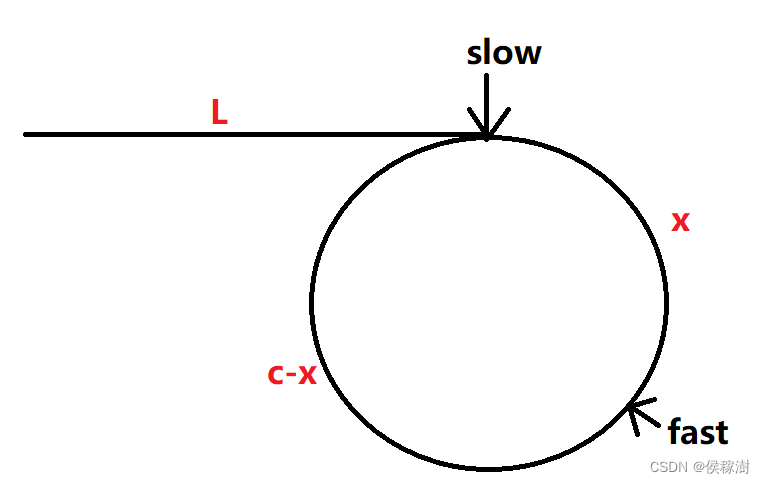
  这个式子也就是说， 如果俩个指针，一个从起点出发，一个从相遇点出发
  二者相遇的地址即为环链表入环点
  转化成代码表示

struct ListNode *detectCycle(struct ListNode *head) {
    struct ListNode * fast = head;
    struct ListNode * slow = head;
    while(fast && fast->next)
    {
        fast = fast->next->next;
        slow = slow->next;
        if(fast == slow)
        {
            struct ListNode * meet = head;
            while(slow != meet)
            {
                slow = slow->next;
                meet = meet->next;
            }
            return meet;
        }
    }
    return NULL;
}

LeetCode142