POJ 2253 Frogger

每条通路中的最长边（集合）的最小值

再在这个最长边的集合里面找最小值。

意思就是说，不仅要去找通路，而且还要找到那条最长边所在的通路。

【坑】那么找到的可能不是每个通路里最长的那条边，

因此只有把每个通路里最长的边先找出来，才能进行比较。

 

首先再读懂题目意思。

重点：只有两个点，（就是题目给出的第一个数据和第二个数据）

剩下的点，全是我们要松弛的对象。

与POJ1797形成对比

问个问题，为什么如下【变式】FLOYD算法可以实现找【每条通路中的最长边（集合）的最小值】，并且输出d[0][1]就是答案。

 

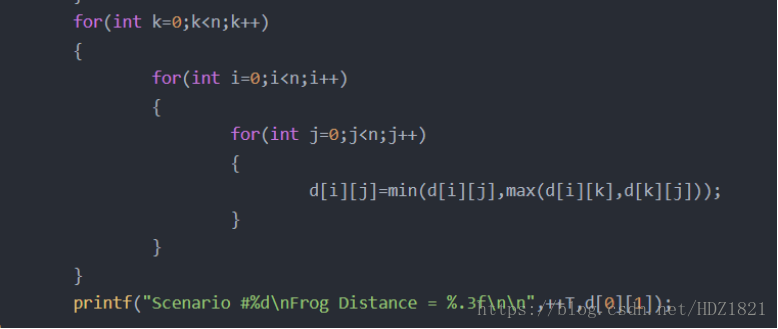
这里的弗洛伊德思想，只要加进去一个点：【i点】控制的是我们要加入的点，既然加入了一个点，那么就意味着多了两条边，于是首先在构成通路的当前新生成的两条边进行比较大小（找最大）。（此时已经形成了一个通路了。）

之后找到了最大值，我们再去和之前的那条边进行比较，（找最小）。

这就是这道题的弗洛伊德的思想。

d[0][1]代表的意思就是，从0点到1点的每条通路中的最长边（集合）的最小值。

#include"stdafx.h"

#include<iostream>

#include<vector>

#include<queue>

#include<string>

#include<algorithm>

#include<math.h>

#include<iomanip>

using namespace std;

 

double  x[300], y[300], m[300][300];

int t, i, j, k, c = 1;

int main()

{

while (cin >> t && t != 0) {

for (i = 0; i < 300; ++i)

for (j = 0; j < 300; ++j)

m[i][j] = 100000000;

for (i = 0; i < t; ++i)

cin >> x[i] >> y[i];

for(i=0;i<t;++i)

for (j = i + 1; j < t; ++j)

{

m[i][j] = m[j][i] = sqrt(abs(x[i] - x[j])*abs(x[i] - x[j]) + abs(y[i] - y[j])*abs(y[i] - y[j]));

//cout << m[i][j] << endl;

}

for (i = 0; i < t; ++i)

for (j = 0; j < t; ++j)

for (k = 0; k < t; ++k)

{

cout << m[j][k] << " " << m[i][k] << " " << m[i][j] << endl;

m[j][k] = min(m[j][k], max(m[i][k], m[i][j]));

}

 

cout << "Scenario #" << c++ << endl;

cout << setiosflags(ios::fixed) << setprecision(3) << "Frog Distance = " << m[0][1] << endl << endl;

}

return 0;

}

 

 

这就要涉及到题目意思了：

而且倘若是迪杰斯特拉，为什么我们也要输出dis[1]，为什么维护的是这个？思想和之前的弗洛伊德思想一模一样。

dis[1]表示的意思也是从0点到1点的每条通路中的最长边（集合）的最小值。