学习资源:深入理解计算机系统 第五章
总述:
编写高效程序,除了众所周知的算法以及数据结构外,还应该考虑代码能被编译器有效优化。本文将罗列几种典型的优化方案。
一.编译器参数
GCC编译器可以调用-og,-o1,-o2,-o3等优化级别来对程序进行优化,而JVM也可以通过一系列指令来禁用或开启某些机制来达到优化的目的。
但是,事实上,有许多的代码是难以优化的:
1.指针运算
c语言的指针是非常难以优化的,如果编译器不能确定两个指针是否指向同一个位置,就必须假设这种情况,这就限制了可能的优化策略。
举例:
void twiddle2(long *xp,long *yp)
{
*xp += *yp;
*xp += *yp;
}
若xp与yp指向同一个位置,那么xp将增加至四倍;
若xp与yp指向不同位置,那么xp将增加至三倍。
因为编译器无法确认是否会产生第一种情况,
所以它无法将代码优化成以下形式。
void twiddle1(long *xp,long *yp)
{
*xp += 2 * *yp;
}
所以为了更快地执行效率,我们应该尽可能按twiddle1的方法去写。
2.函数调用
若函数在调用过程中,修改了全局程序状态的一部分,那么编译器会假设最糟糕的情况,并保持所有函数的调用不变。
举例:
long counter = 0;
long f() {
return counter++;
}
long func1(){
return f() + f() + f() + f();
}
long func2(){
return f() * 4;
}
fun1与fun2返回值不同,所以编译器是不会把fun1优化成fun2
优化方案:内联函数替换
将对函数的调用替换为函数体
long func1(){
long t = counter ++;
t += counter ++;
t += counter ++;
t += counter ++;
return t;
}
按这样子修改,编译器就会进行优化
long func1(){
long t = 4 * counter +6;
counter += 4;
return t;
}
GCC编译器会尝试自行进行内联函数替换,但是只能在单文件中,而且必须开启更高的优化等级,并且无法进行断点调试。所以还请各位自行进行内联函数替换。
二.循环展开
在循环的时候,每次迭代多个元素,能减少循环的迭代次数。
减少了不直接有助于程序结果的操作数量,例如循环索引计算和条件分支;提供了一些方法可以进一步优化代码。
void psum1 (float a[], float p[], long n)
{
long i;
p[0] = a[0];
for(i = 1, i < n, i++)
p[i] = p[i-1] + a[i];
}
//2*1循环展开
void psum2(float a[], float p[], long n)
{
long i;
p[0] = a[0];
for( i=1; i < n-1; i +=2){
float mid_value = p[i-1] + a[i];
p[i] = mid_value;
p[i+1] = mid_vlaue + a[i+1];
}
if (i < n)
p[i] = p[i-1] + a[i];
}
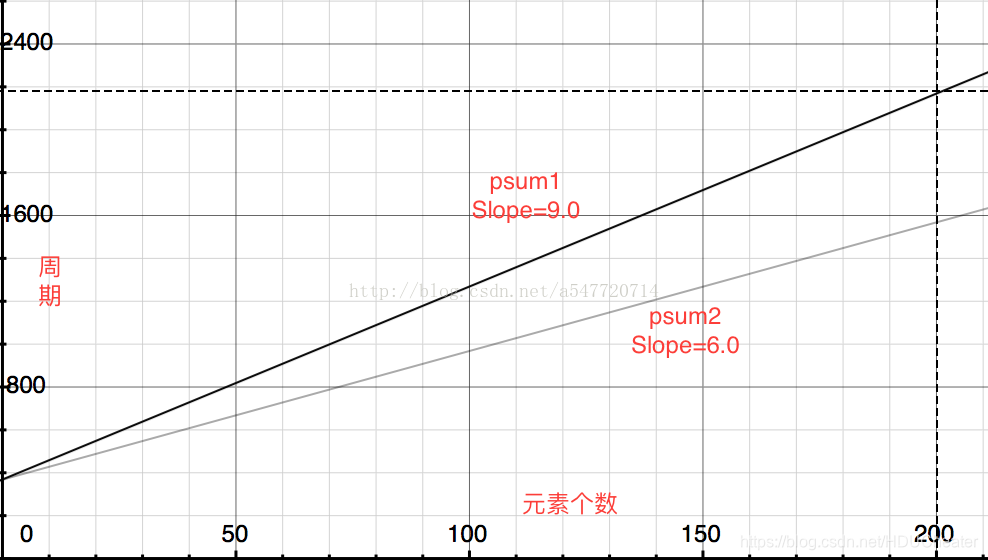
前者运行时间 368 + 9.0n,后者运行时间 368 + 6.0n
三.泛型优化
将一个向量中所有元素合并成一个值
通过不同的宏定义来执行不同的运算
#define IDENT 0
#define OP +
#define IDENT 0
#define OP *
void combine1(vec_ptr v, data_t *dest)
{
long i;
*dest = IDENT;
for(i = 0; i < vec_length(v); i++)
data_t val;
get_vec_element(v, i, &val);
*dest = *dest OP val;
}
}

四.代码移动
将某些不会改变的并且要被调用多次的值 赋值 给局部变量,可以提升程序效率。
举例:
循环里的 i < xx.length 修改为 int len = xx.length;for(…;i<len;i++) 能提升程序效率。
五.消除不必要的内存引用
举例:
void combine4(vec_ptr v, data_t *dest)
{
long i;
long length = vec_length(v);
data_t *data = get_vec_start(v);
data_t acc = IDENT;
for(i = 0; i < length; i++)
acc = acc + data[i];
*dest = acc;
}
如果直接对dest进行运算,每次迭代需要两次读一次写,转化为临时变量后,只需要一次读。

六.并行
对于一个可结合和可交换的合并运算来说,比如整数加法和乘法,我们可以通过将一组合并运算分割成两个或更多的部分,并在最后合并结果来提高性能。
//2*2循环展开
void combine6(vec_ptr v, data_t *dest)
{
long i;
long length = vec_length(v);
long limit = length-1;
data_t *data = get_vec_start(v);
data_t acc0 = IDENT;
data_t acc1 = IDENT;
for(i=0; i<limit; i++){
acc0 = acc0 OP data[i];
acc1 = acc1 OP data[i+1];
}
for(; i<length; i++){
acc0 = acc0 OP data[i];
}
*dest = acc0 OP acc1;
}
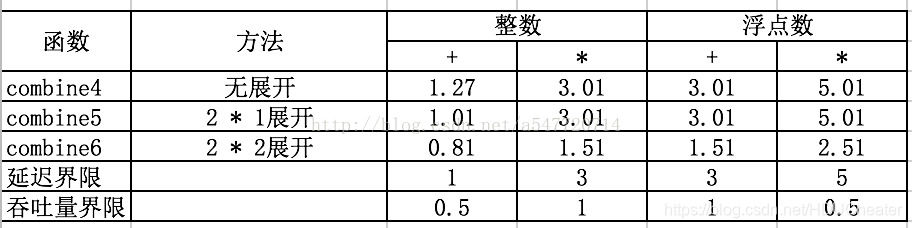
七.重新结合运算
void combine7(vec_ptr v, data_t *dest)
{
long i;
long length;
long limit = length - 1;
data_t *data = get_vec_start(v);
data_t acc = IDENT;
for( i=0; i<limit; i+=2){
acc = acc OP (data[i] OP data[i+1]);
//acc = (acc OP data[i]) OP data[i+1];
}
for(; i<length; i++){
acc = acc OP data[i];
}
*dest = acc;
}
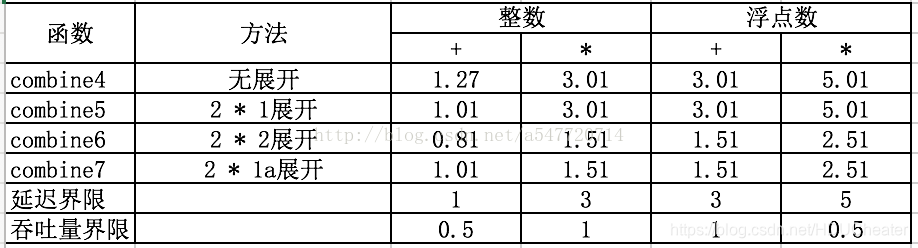
整数加的性能与combine5(K * 1展开版本)相同,其他三种情况则与使用了并行累计变量的combine6版本相同,是K*1扩展性能的2倍,这些情况已经突破了延迟界限造成的限制。
因为每次迭代内的第一个乘法(data[i] OP data[i+1])都不需要等待前一次迭代的累计值就可以执行。
对于整数加法和乘法,这些运算可结合,这表示对于重新变换顺序对结果没有影响,对于浮点数情况,必须再次评估这种重新结合是否有可能严重影响结果。
终上所述就是利用循环展开,降低循环次数(K1),添加多个累积变量(K2)来使用“K1 * K2”循环展开。





















 938
938

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








